The current flowing through wire depends on time as, I=3t2+2t+5
The charge flowing through the cross - section of the wire in time t=0 to t=2 second is
22 C
20 C
18 C
5 C
The correct Answer is:A
To find the charge flowing through the cross-section of the wire from time t=0 to t=2 seconds, we start with the given current function:
I(t)=3t2+2t+5
Step 1: Relate current to charge
The current I is defined as the rate of flow of charge, which can be expressed mathematically as:
I=dqdt
This means that the differential charge dq can be expressed as:
dq=Idt
Step 2: Substitute the expression for current
Substituting the expression for current into the equation gives:
dq=(3t2+2t+5)dt
Step 3: Integrate to find total charge
To find the total charge Q that flows from t=0 to t=2, we need to integrate dq:
Q=∫20(3t2+2t+5)dt
Step 4: Perform the integration
We can break this integral into three parts:
Q=∫203t2dt+∫202tdt+∫205dt
Calculating each integral separately:
1. For ∫3t2dt:
∫3t2dt=3⋅t33=t3(evaluated from 0 to 2)
=23−03=8
2. For ∫2tdt:
∫2tdt=2⋅t22=t2(evaluated from 0 to 2)
=22−02=4
3. For ∫5dt:
∫5dt=5t(evaluated from 0 to 2)
=5⋅2−5⋅0=10
Step 5: Combine the results
Now, we combine the results from the three integrals:
Q=8+4+10=22coulombs
Conclusion
The total charge flowing through the cross-section of the wire from t=0 to t=2 seconds is:
22coulombs
The current I is defined as the rate of flow of charge, which can be expressed mathematically as:
Substituting the expression for current into the equation gives:
To find the total charge Q that flows from t=0 to t=2, we need to integrate dq:
We can break this integral into three parts:
∫3t2dt=3⋅t33=t3(evaluated from 0 to 2)
=23−03=8
∫2tdt=2⋅t22=t2(evaluated from 0 to 2)
=22−02=4
∫5dt=5t(evaluated from 0 to 2)
=5⋅2−5⋅0=10
Now, we combine the results from the three integrals:
The total charge flowing through the cross-section of the wire from t=0 to t=2 seconds is:
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example
65 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
The current through a wire depends on time as i=(2+3t)A. Calculate the charge crossed through a cross section of the wire in 10sec.
View SolutionThe current through a wire depends on time as
I=i0+αt,
where i0=10Aandα=4As−1.Find the charge crossed through a section of the wire in 10 second
View Solution
Knowledge Check
A current in a wire is given by the equation, . I=2t2−3t+1, the charge through cross section of : wire in time interval t=3s to t=5s is
A32.33CB43.34CC45.5CD42C
The current through a wire depends on time as, i=(10+4t) Here , i is ampere and t in seconds. Find the charge crossed through section in time interval between t=0 to t=10s.
View SolutionThe current through a wire depends on time as
I=i0+αt,
where i0=10Aandα=4As−1.Find the charge crossed through a section of the wire in 10 second
View SolutionCurrent passing through a wire decreases linearly from 10A to 0 in 4s. Find total charge flowing through the wire in the given time interval.
View SolutionThe plot represents the flow of current through a wire at three different times. The ratio of charges flowing through the wire at different time is
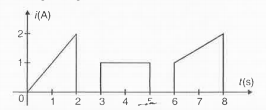
View Solution(a) The amount of charge passed in time t through a cross-section of wire is
q=αt−βt2
where α and β are constant.
(i) Find current in terms of time t.
(ii) Sketch i versus t graph.
(b) The current through a wire depends on time as
i=4+3t+2t2
Find the charge crossed through a section of wire in 6sec.
View SolutionThe current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
View SolutionThe current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
View Solution