Consider a spherical shell of radius R wil a total charge +Q uniformly spread on its surface (centre of the shell lies at the origin x =0) Two point charge +q and -q are brought, one after the other, from far away and placed at x=−a/2 and x=+a/2(a<R) respectively. Magnitude of the work done in this process is
a. (Q+q)2/4πε0a
b. zero
c. q2/4πε0a
d. Qq/4πε0a
The correct Answer is:C
To solve the problem, we need to calculate the work done in bringing two point charges (+q and -q) from infinity to specific positions near a uniformly charged spherical shell. Here's a step-by-step breakdown of the solution:
Step 1: Understand the Setup
We have a spherical shell of radius R with a total charge +Q uniformly spread on its surface. The center of the shell is at the origin (0,0,0). We need to bring a charge +q to the position x=−a2 and a charge −q to the position x=+a2, where a<R.
Step 2: Calculate the Work Done to Bring Charge +q
The work done W1 in bringing the charge +q from infinity to the point x=−a2 can be calculated using the formula:
W1=q⋅V
where V is the electric potential at the point x=−a2.
For a uniformly charged spherical shell, the electric potential inside the shell (at any point within the radius R) is given by:
V=kQR
where k=14πϵ0.
Thus, the work done in bringing the charge +q is:
W1=+q⋅kQR
Step 3: Calculate the Work Done to Bring Charge -q
Next, we bring the charge −q to the position x=+a2. The potential at this point is still the same as at the previous point because it is also inside the shell:
V′=kQR
The work done W2 in bringing the charge −q is:
W2=−q⋅V′=−q⋅kQR
Step 4: Calculate the Total Work Done
The total work done W in bringing both charges is the sum of the work done for each charge:
W=W1+W2
Substituting the values we found:
W=(+q⋅kQR)+(−q⋅kQR)
This simplifies to:
W=kQqR−kQqR=0
Step 5: Magnitude of Work Done
Since the total work done is zero, the magnitude of the work done is:
|W|=0
Final Answer
The magnitude of the work done in this process is 0.
---
We have a spherical shell of radius R with a total charge +Q uniformly spread on its surface. The center of the shell is at the origin (0,0,0). We need to bring a charge +q to the position x=−a2 and a charge −q to the position x=+a2, where a<R.
The work done W1 in bringing the charge +q from infinity to the point x=−a2 can be calculated using the formula:
W1=q⋅V
where V is the electric potential at the point x=−a2.
V=kQR
where k=14πϵ0.
W1=+q⋅kQR
Next, we bring the charge −q to the position x=+a2. The potential at this point is still the same as at the previous point because it is also inside the shell:
V′=kQR
W2=−q⋅V′=−q⋅kQR
The total work done W in bringing both charges is the sum of the work done for each charge:
W=W1+W2
Substituting the values we found:
W=(+q⋅kQR)+(−q⋅kQR)
This simplifies to:
W=kQqR−kQqR=0
Since the total work done is zero, the magnitude of the work done is:
|W|=0
The magnitude of the work done in this process is 0.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4410videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4520videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4220videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2
A thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R/2 from the centre of the shell is
View SolutionA spherical shell having charge +Q (uniformly distributed) and a point charge +q0 are placed as shown. Find the force between shell and the point charge (r>>R).
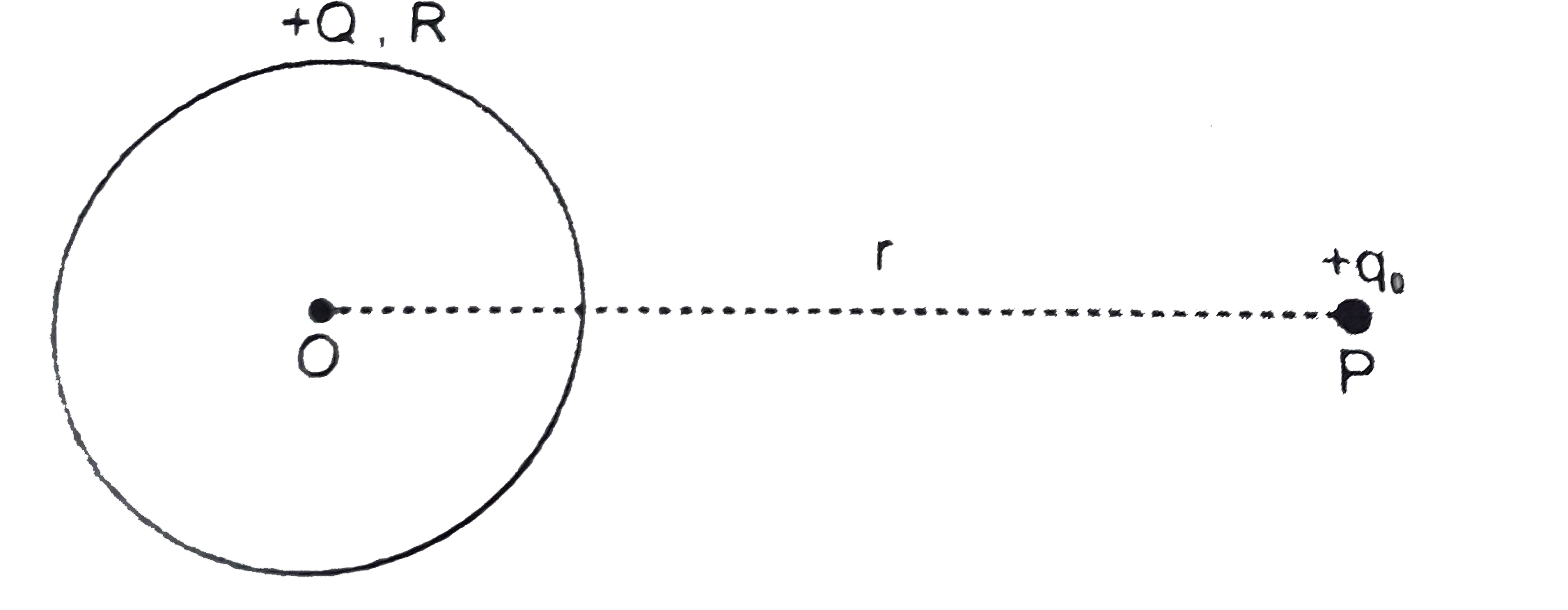 View Solution
View SolutionA spherical shell of radius R is given charge 3q on its surface and a point charge q is placed at distance R/2 from its centre C. Also there is a charge 2q placed outside the shell at a distance of 2R as shown. Then
 View Solution
View SolutionA thin spherical shell radius of R has a charge Q uniformly distributed on it. At the centre of the shell, a negative point charge -q is placed. If the shell is cut into two identical hemispheres, still equilibrium is maintained. Then find the relation between Q and q?
 View Solution
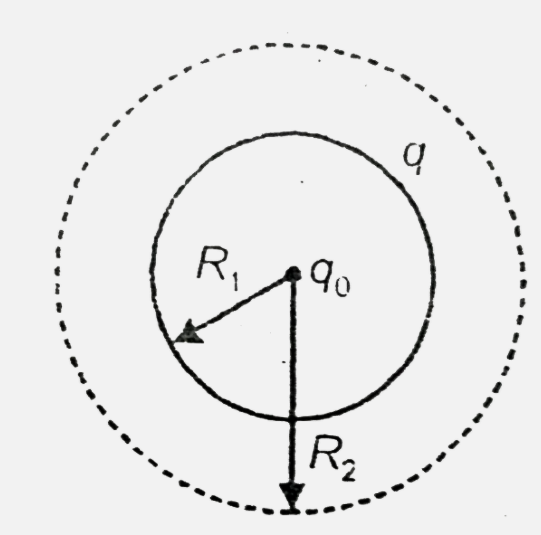
View SolutionA spherical shell of radius R1 with uniform charge q is expanded to a radius R2. Find the work performed by the electric forces in this process.
View SolutionA spherical shell of radius R carries a uniformly distributed charge q. The electrical forces arising cause the ex-pansion of the shell. Find the mechanical stress in the shell.
 View Solution
View Solution