The dimensions of Stefan-Boltzman constant σ can be written in terms of Plank's constant h. Boltzmann constant kB and the speed of light c as σ=hαKbBcY. Here
α=3,β=4andγ=−3
α=3,β=−4andγ=2
α=−3,β=4andγ=−2
α=2,β=−3andγ=−1
The correct Answer is:C
To find the values of α, β, and γ in the equation for the Stefan-Boltzmann constant σ=hαkβBcγ, we will start by writing down the dimensions of each constant involved.
Step 1: Write down the dimensions of the Stefan-Boltzmann constant σ
The Stefan-Boltzmann constant σ has the units of power per unit area per unit temperature to the fourth power. In SI units, it can be expressed as:
σ=Wm2⋅K4
Since W=J/s and J=kg⋅m2/s2, we can rewrite this as:
σ=kg⋅m2/s2m2⋅K4=kgs3⋅K4
Thus, the dimensions of σ can be expressed as:
(σ)=M1L0T−3Θ−4
Step 2: Write down the dimensions of Planck's constant h
Planck's constant h has the units of energy multiplied by time:
h=J⋅s=kg⋅m2s2⋅s=kg⋅m2⋅s−1
Thus, the dimensions of h are:
(h)=M1L2T−1
Step 3: Write down the dimensions of the Boltzmann constant kB
The Boltzmann constant kB has the units of energy per temperature:
kB=JK=kg⋅m2/s2Θ
Thus, the dimensions of kB are:
(kB)=M1L2T−2Θ−1
Step 4: Write down the dimensions of the speed of light c
The speed of light c has the units of distance per time:
c=ms=L1T−1
Thus, the dimensions of c are:
(c)=L1T−1
Step 5: Combine the dimensions
Now we can express the dimensions of σ in terms of h, kB, and c:
(σ)=(h)α(kB)β(c)γ
Substituting the dimensions we found:
M1L0T−3Θ−4=(M1L2T−1)α(M1L2T−2Θ−1)β(L1T−1)γ
Step 6: Equate the powers of each dimension
Now we will equate the powers of M, L, T, and Θ:
1. For M:
1=α+β(1)
2. For L:
0=2α+2β+γ(2)
3. For T:
−3=−α−2β−γ(3)
4. For Θ:
−4=−β(4)
Step 7: Solve the equations
From equation (4):
β=4
Substituting β into equation (1):
1=α+4⟹α=−3
Now substituting α and β into equation (2):
0=2(−3)+2(4)+γ⟹0=−6+8+γ⟹γ=−2
Final Result
Thus, we have:
α=−3,β=4,γ=−2
1=α+β(1)
0=2α+2β+γ(2)
−3=−α−2β−γ(3)
−4=−β(4)
β=4
1=α+4⟹α=−3
0=2(−3)+2(4)+γ⟹0=−6+8+γ⟹γ=−2
α=−3,β=4,γ=−2
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4410videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4520videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4220videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
The radiation emitted per unit time by unit area of a black body at temperature T is σT4 wehre σ is the Stefan-Boltzmann constant. The constant σ can also be expressed in terms of Boltmann's constant (k), Planck's constant (h) and speed of light (3) as σ=Akαhβcγ where A,α,β and γ are dimensionless constants. The set (α,β,γ) is givne by
View SolutionExpression for time in terms of G (universal gravitational constant), h (Planck constant) and c (speed of light) is proportional to:
View SolutionThe dimension of stooping potential V0 in photoelectric effect In units of Planck's constant 'h', speed of light 'c' and Gravitational constant 'G' and ampere A is:
View SolutionThe dimension of σb4 (where σ is Stefan's constant and b is Wien's constant) are [ML4T−3] is it true.
View SolutionDefine the following terms :
(a) Molarity
(b) Molal elevation constant (Kb)View SolutionThe quantity PVkBT represents the (kB:Boltzmann constant)
View SolutionWhich of the following is dimensionless
(a) Boltzmann constant (b) Planks constant
(c) Poissons ratio (d) Relative densityView SolutionThe radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
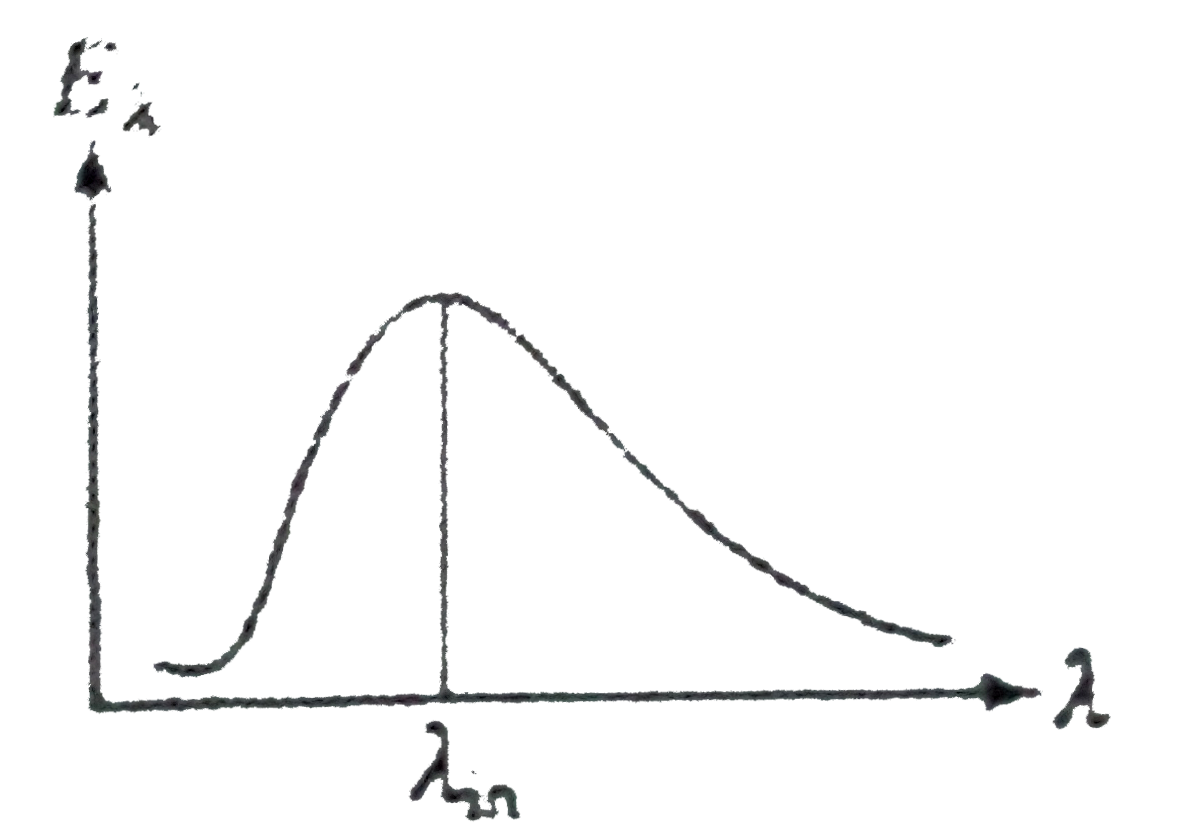
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) isView SolutionThe constant 'a' Mosely's law √v=a(Z−b) for kαX−rays is related to Rydberg constant R as ('c' is the speed of light)
View SolutionThe average thermal energy for a mono-atomic gas is: (kB is Boltzmann constant and T, absolute temperature)
View Solution

