There is layer of medium of variable refractive index μ=√2−1√2y (where 0≤t<1/2) sandwitched between the layer of glass and air A beam of light travelling in air at an angle 45∘ has a width Δω. When the beam enters the layer of glass its width becomes : (μglass=√2)
a. √32Δω
b. √23Δω
c. √13Δω
d. Δω
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the setup
We have a layer of medium with a variable refractive index given by:
μ=√2−1√2y
This layer is sandwiched between glass (with refractive index μglass=√2) and air (with refractive index μair=1). A beam of light enters the medium from air at an angle of 45∘.
Step 2: Apply Snell's Law at the air-glass interface
Using Snell's Law:
μ1sini=μ2sinr
where:
- μ1=1 (air)
- i=45∘
- μ2=√2 (glass)
- r is the angle of refraction in glass.
Substituting the values:
1⋅sin(45∘)=√2⋅sin(r)
1√2=√2⋅sin(r)
sin(r)=12
Thus, r=30∘.
Step 3: Determine the angle of incidence in the variable medium
Since the beam of light enters the variable refractive index medium, we need to find the angle of incidence in this medium. The angle of incidence can be calculated as:
θ=90∘−r=90∘−30∘=60∘
Step 4: Calculate the width of the beam in the variable medium
Let h be the thickness of the variable medium. The width of the beam in the variable medium can be expressed as:
Δω′=h⋅tan(θ)
where θ=60∘:
Δω′=h⋅tan(60∘)=h⋅√3
Step 5: Relate the width in air to the width in glass
In air, the width of the beam is given by:
Δω=h⋅tan(45∘)=h
Step 6: Find the relationship between the widths
Now, we can relate the widths:
Δω′=√3⋅Δω
Conclusion
Thus, the width of the beam when it enters the layer of glass becomes:
Δω′=√32Δω
We have a layer of medium with a variable refractive index given by:
μ=√2−1√2y
This layer is sandwiched between glass (with refractive index μglass=√2) and air (with refractive index μair=1). A beam of light enters the medium from air at an angle of 45∘.
Using Snell's Law:
μ1sini=μ2sinr
where:
- μ1=1 (air)
- i=45∘
- μ2=√2 (glass)
- r is the angle of refraction in glass.
1⋅sin(45∘)=√2⋅sin(r)
1√2=√2⋅sin(r)
sin(r)=12
Thus, r=30∘.
Since the beam of light enters the variable refractive index medium, we need to find the angle of incidence in this medium. The angle of incidence can be calculated as:
θ=90∘−r=90∘−30∘=60∘
Let h be the thickness of the variable medium. The width of the beam in the variable medium can be expressed as:
Δω′=h⋅tan(θ)
where θ=60∘:
Δω′=h⋅tan(60∘)=h⋅√3
In air, the width of the beam is given by:
Δω=h⋅tan(45∘)=h
Now, we can relate the widths:
Δω′=√3⋅Δω
Thus, the width of the beam when it enters the layer of glass becomes:
Δω′=√32Δω
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.46
11 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.47
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.44
10 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A system of coordinatees is drawn in a medium whose refractive index vaires as μ=21+Y2 where 0≤y≤1. A ray of light is incident at origin at an angle 60∘ with y-axis as shown in figure. At point P, the ray becomes parallel to x-axis, the volue of H is -

View SolutionWhen light travels from glass to air, the incident angle is θ1 and the refracted angle is θ2. The true relation is
View Solution
Knowledge Check
Critical angle of glass is θ1 and that of water is θ2. The critical angle for water and glass surface would be (μg=3/2,μw=4/3)
Aless than θ2Bbetween θ1 and θ2Cgreater than θ2Dless than θ1Critical angle of glass is θ1 and that of water is θ2. The critical angle for water and glass surface would be (μg=3/2,μw=4/3)
Abetween θ1 and θ2Bgreater than θ2Cless than θ1Dless than θ2
A beam of light falls on a glass plate (μ=3/2) of thickness 6.0 cm at an angle of 60∘. Find the deflection of the beam on passing through the plate. (in cm).
View SolutionA thin lens made of a material of refractive indexμ2 has a medium of refractive index μ1 on one side and a medium of refractive index on the other side. The lens is biconvex and the two radii of curvature have equal magnitude R. A beam of light travelling parallel to the principal axis is incident on the lens. Where will the image be formed if the beam is incident from (a) the medium p, and (b) from the medium μ3?
View SolutionA glass prism has refractive index √2 and refracting angle 30∘ . One of the refracting surface of the prism is silvered. A beam of monchromatic light will retrace it path it its angle of incidence on the unsilvered refracting surface of the prism is
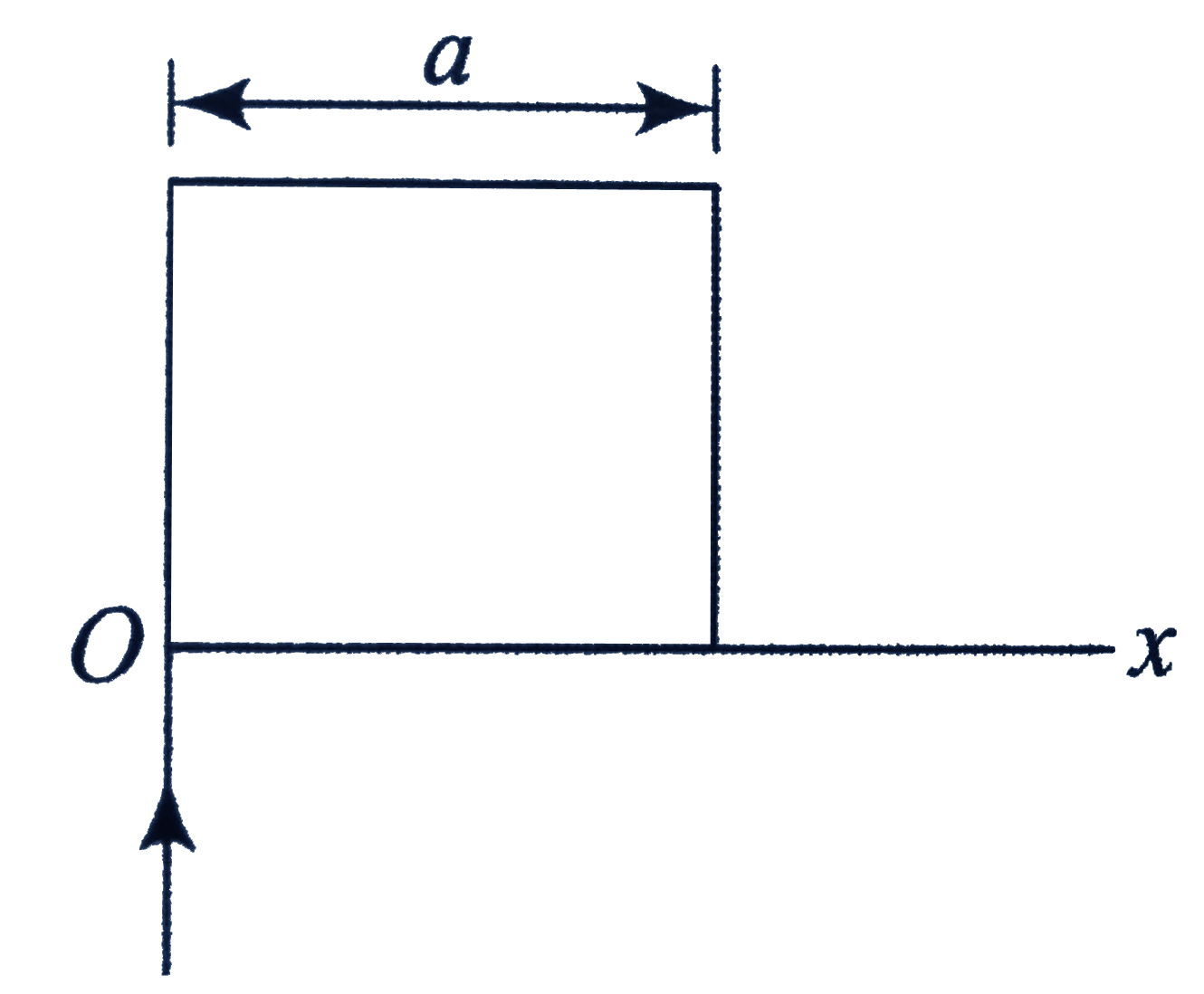
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
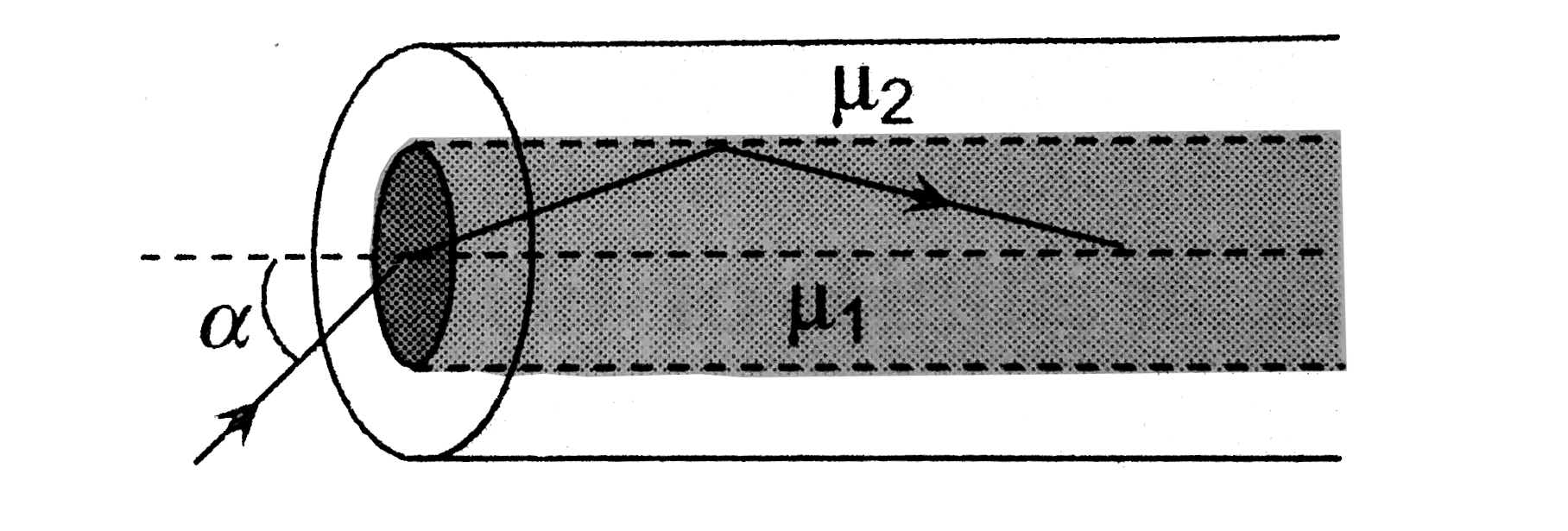
View SolutionAn optical fibre consists of core of μ1 surrounded by a cladding of μ2<μ1. A beam of light enters from air at an angle α with axis of fibre. The highest α for which ray can be travelled through fibre is
View SolutionA prism having refractive index √2 and refractive angle 30∘ has one of the refractive surfaces polished. A beam of light incident on the other surfaces will trace its path if the angle of incidence is
View Solution
