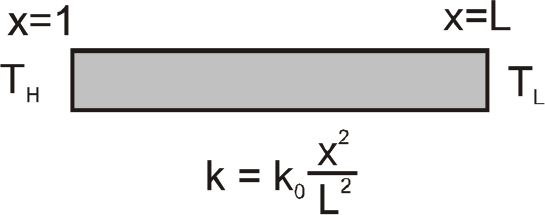
A rod of uniform cross-section but non-uniform thermal conductivity which vary as k=k0x2L2(1≤x≤L) (as shown in figure) is kept between fixed temperature difference for a long time. Select the correct options(s)



The correct Answer is:A, D
I=k0x2L2AdTdx⇒T∫THdT=iL2k0Ax∫ldxx2
T−TH=iL2k0A[1x]x1.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.46
11 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.47
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.44
10 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Figure shows a metal rod of uniform cross section A, with variable thermal conductivity given by k(x)=k0sec(π6Lx). If the end A is maintained at temperature T0, the rod carries a thermal current I0 (from B to A) in steady state and I0Lk0AT0=π3, find the temperature of the end B of the rod. Let's say this temperature is kT0, find integer value k.

View SolutionFigure shown two adiabatic vessels, each containing a mass m of water at different temperature. The ends of a metal rod of length L, area of cross section A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperature in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.

View Solution
Knowledge Check
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1Two chunks of metal with heat capacities C1 and C2, are interconnected by a rod length l and cross-sectional area S and fairly low heat conductivity K. The whole system is thermally insulated from the environment. At a moment t=0 the temperature difference betwene the two chunks of metal equals (ΔT)0. Assuming the heat capacity of the rod to be negligible, find the temperature difference between the chucks as a function of time.
AT0exp(−KA(C1+C2)tC1C2)BT0exp(−KA(C1+C2)C1C2)CT0exp(KA(C1+C2)tC1C2)DT0exp(KA(C1+C2)t2C1C2)
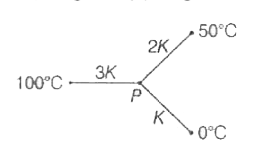
Three rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below
Then , the temperature of the junction in steady - state is
View SolutionTwo ends of a rod of non uniform area of cross section are maintained at temperature T1and T2 (T1>T2) as shown in the figure
If l is heat current through the cross-section of conductor at distance x from its left face, then the variation of l with x is best represented by
View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
View SolutionFigure shows a large tank of water at a constant temperature θ0 and a small vessel containing a mass m of water at an initial temperature θ1(<θ0). A metal rod of length L, area of cross section A and thermal conductivity K connects the two vessels. Find the time taken for the temperature of the water in the smaller vessel to become θ2(θ1<θ2<θ0) . Specific heat capacity of water is s and all other heat capacities are negligible.

View SolutionThe end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
View SolutionThree rods of identical cross - section and length are made of three different material of thermal conductivity k1,k2 and k3 respectively. They are joined together at their ends to make a long rod (See figure). One end of the long rod is maintained at 100∘C and the other at 0∘C ( See figure ). If the joints of the rod are at 70∘C and 20∘C in steady state and there is no loss of energy form the surface of the rod, the correct relationship between k1,k2 and k3 is
View Solution
