A uniform rod AB of mass m and length l is hinged at its mid point C. The left half (AC) of the rod has linear charge density −λ and the right half (CB) has +λ where λ is constant. A large non conducting sheet of uniform surface charge density σ is also present near the rod. Initially the rod is kept perpendicular to the sheet. The end A of the rod is initialy at a distance d. Now the rod is rotated by a small angle in the plane of the paper and released. Prove that the rod will perform SHM and find its time period.

The correct Answer is:T=2π√2m∈03λσ
The sheet produces a uniform electric field E=σ2∈0 towards right. The part AC and BC will experience electric force F as shown. They can be considered to be activing at the mid points of those parts respectively. The rod will experience torque about the point c in the anticlockwise direction
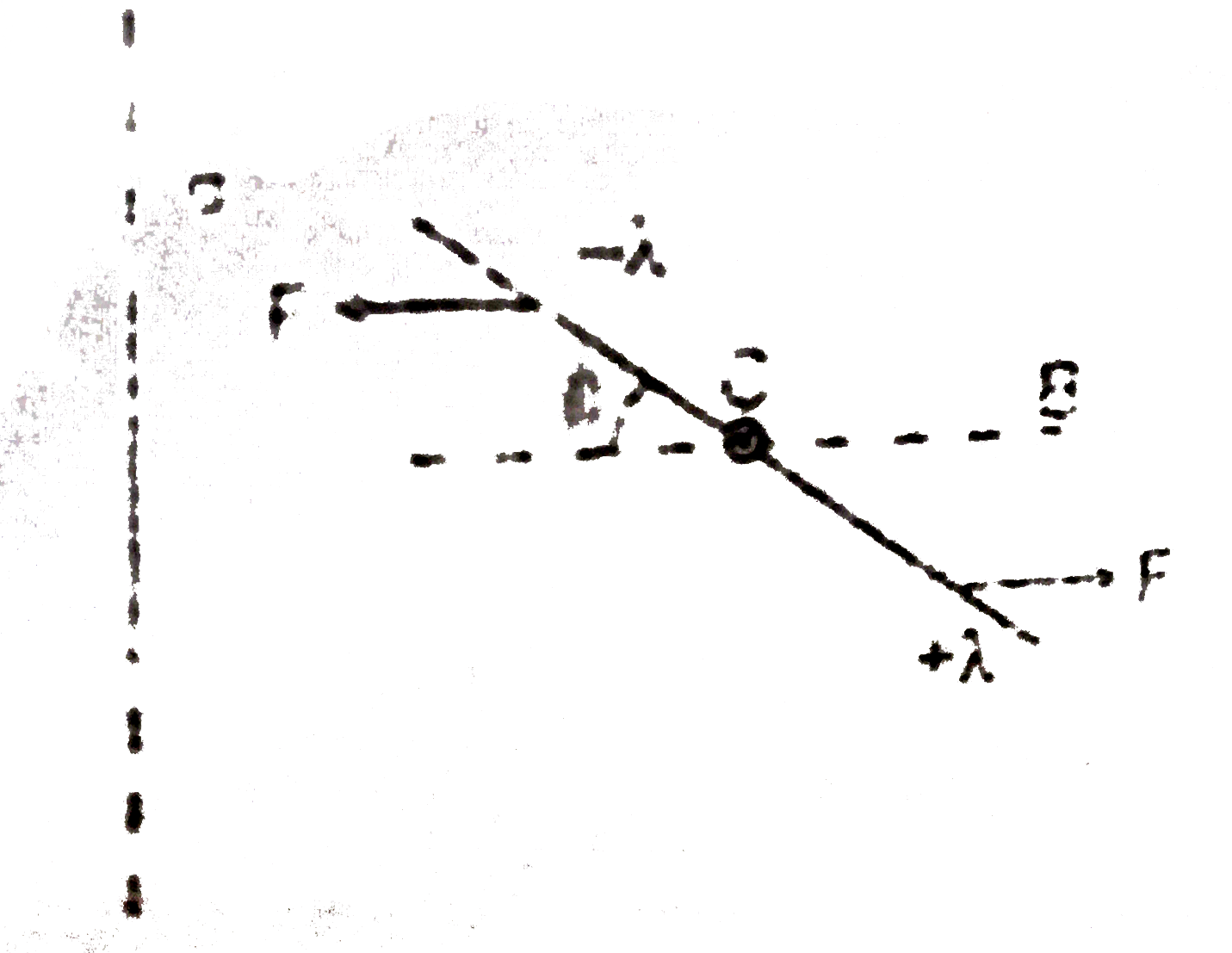
whose magnitude is τ=Fl2sinθ=Fl2θ:
But F=λl2.σ2∈0=λlσ4∈0
τ=(λl2σ8∈0)θ
Now since τ is towards the mean position & τ∝θ
∴ it will do SHM → Hence proved
& τ=1∝=λl2σ8∈0
⇒ml2sgma12α=λl2σ8∈0α
α=(3λσ2m∈0)θ
∴ω2=3λσ2m∈0⇒(2πT)2
⇒T=2π√2m∈03λσ
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.61
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.62
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.59
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Find out energy stored in an imaginary cubical volume of side a in front of a infinitely large non-conducting sheet of uniform charge density σ.
View SolutionA large nonconducting sheet M is given a uniform charge density. Two unchared small metal rods A and B are placed near the sheet as shown in figure

View SolutionA large nonconducting sheet M is given a uniform charge density. Two unchared small metal rods A and B are placed near the sheet as shown in figure

View SolutionA large sheet carries uniform surface charge density σ . A rod of length 2l has a linear charge density λ on one half and −λ on the second half. The rod is hinged at the midpoint O and makes an angle θ with the normal to the sheet. The torque experience by the rod is
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Normal reaction by ground on the rod

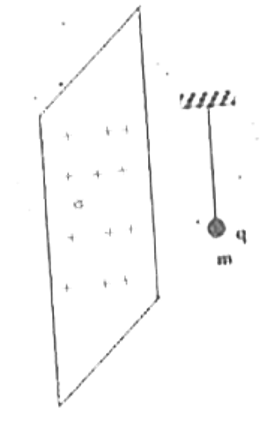
View SolutionA small charged particle of mass m and charge q is suspended by an insulated thread in front of a very large conducting charged sheet of uniform surface density of charge σ. The angle made by the thread with the vertical in equilibrium is
View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The length of the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View Solution
