Consider a U-shaped frame with a sliding wire of length l and mass 'm' on its arm. It is dipped in a soap solution, taken out and placed in vertical position as shown in figure. Choose minimum value of m so that does not descent (Surface tension of soap solution is S)

The correct Answer is:D
For wire to be in equilibrium,
mg=2Sl⇒m=2Slg
For mass less than 2Slg it will move upward So amongst the options Sl4g is the minimum mass.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.709videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.7110videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.689videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
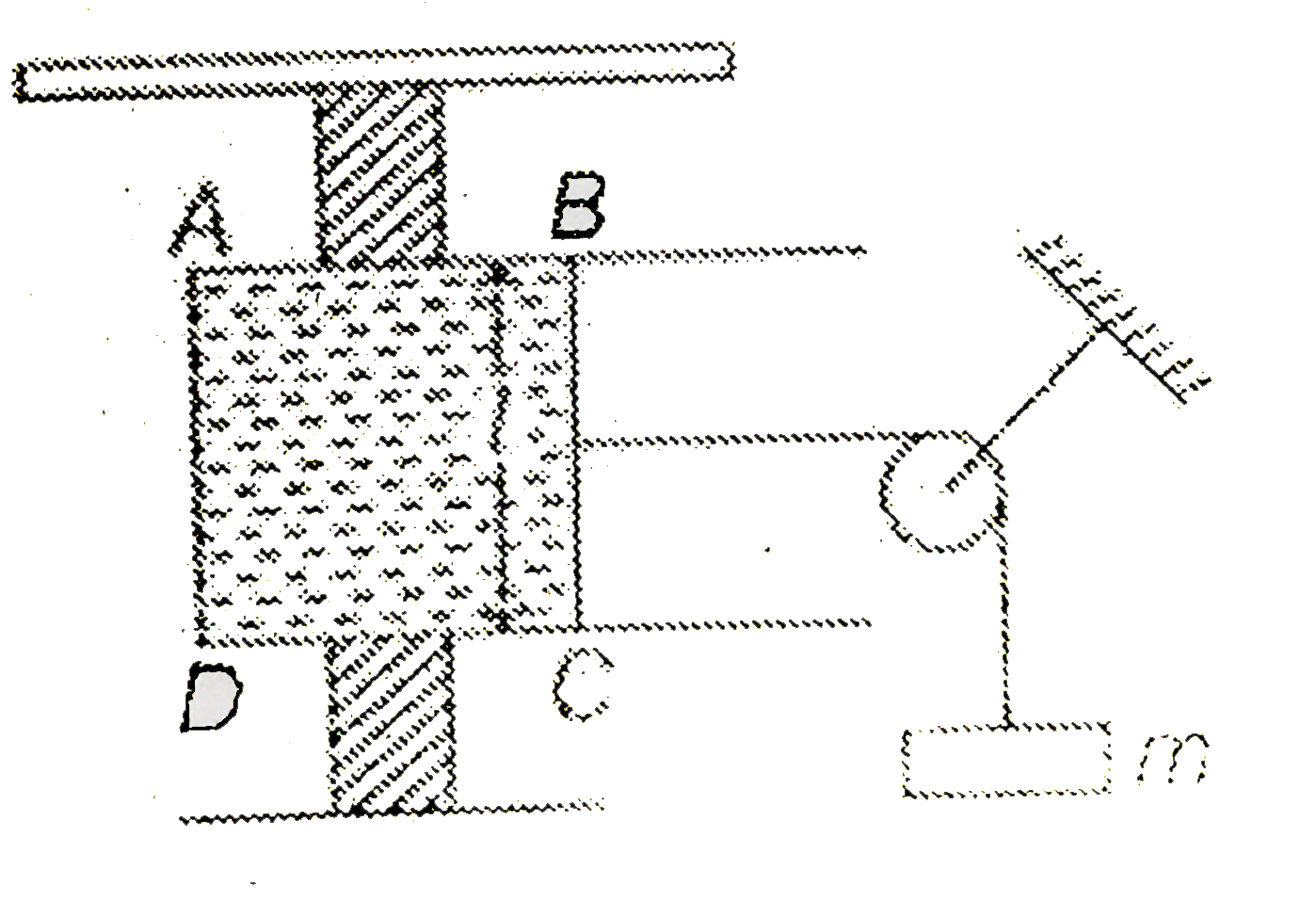 View Solution
View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
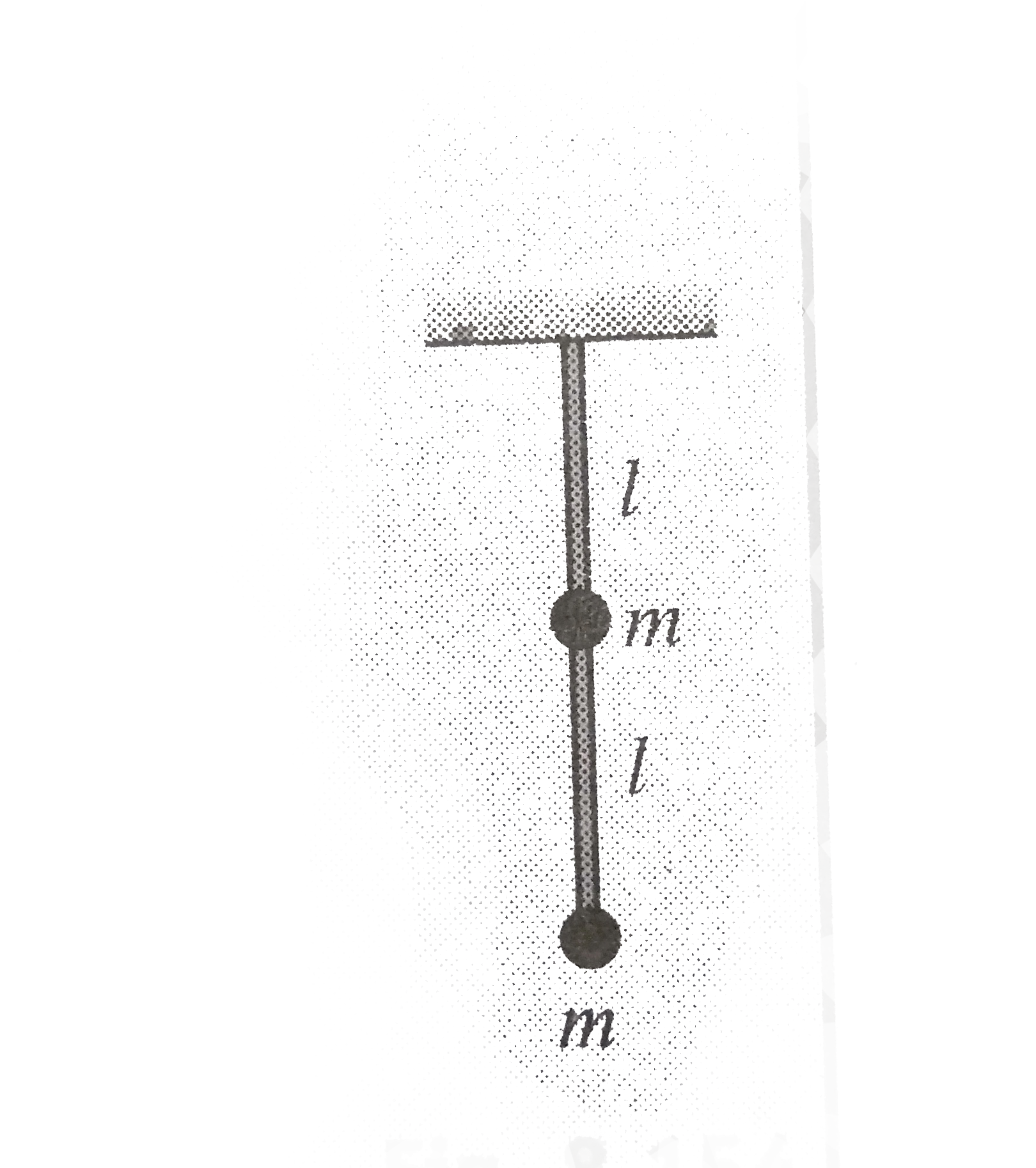 View Solution
View SolutionA rod of mass m and length L is pivoted at a point O and kept in horizontal position as shown in figure. Now it is released from this position so that it can rotates freely about the point O in downward direction. When it becomes vertical
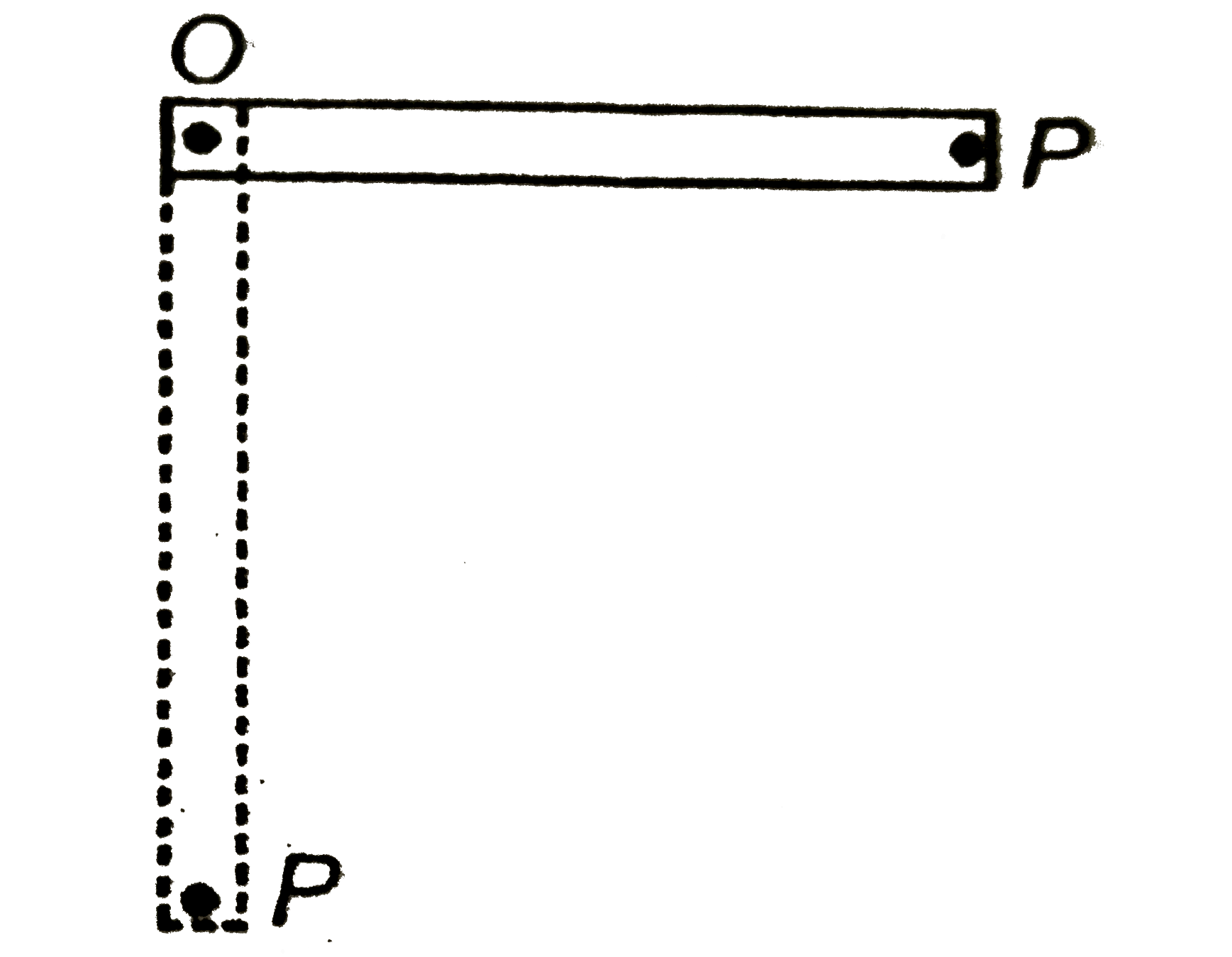 View Solution
View SolutionA rod PQ of length 'L' is hung from two identical wires A and B. A block of mass 'm' is hung at point R of the rod as shown in figure. The value of 'x' so that the fundamental mode in wire A is in resonance with first overtone of B is
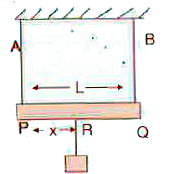 View Solution
View SolutionA wire of mass 5 gm is kept horizontally on the surface of water. What ist he minimum length of the wire so that it does not break the surface film.Surface tension =72×10−3N/m
View SolutionA uniform slender bar B of mass m and length L supported by a firctionless pivot at A is released from rest at its vertical position as shown the figure. Calculate the reaction at pivot when the bar just acquires the horizontal position shown dotted.
 View Solution
View SolutionA thin and light thread of sufficient length L is attached to a wire frame. The frame (along with the thread) is dipped into soap solution. When the frame is taken out of the solution, the thread takes the form of a semicircle with a soap film extending between the frame and the thread as shown in the figure (a). Now the thread is deformed into two semicircles by applying a force of F at the middle of the thread, as a result the film gets strectched as shown in the figure. (b). Calculate the surface tension of the soap solution.
 View Solution
View Solution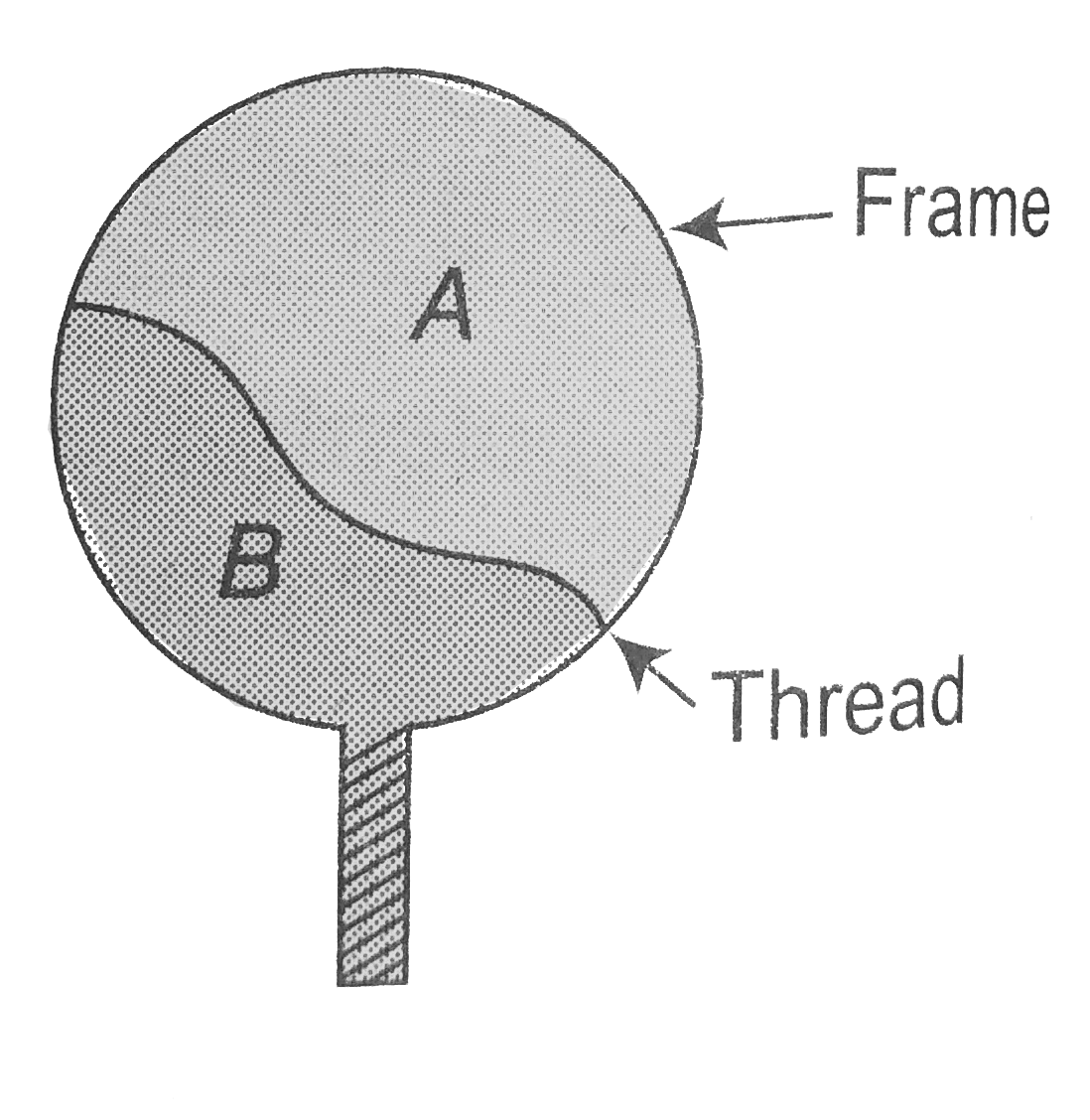
A thread is tied slightly loose to a wire frame as in figure and the frame is dipped into a soap solution and taken out . The frame is comletely covered with the film. When the portion A puntured with a pin The thread.View SolutionA film of soap solution is formed on a loop frame loop of 6.28cm long thread is gently put on the film and the film is broken with a needle inside the loop. The tread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030n/m.
View SolutionA light wire AB of length 10 cm can slide on a vertical frame as shown in figure. There is a film of soap solution trapped between the frame and the wire. Find the load W that should be suspended from the wire to keep it in equilibrium. Neglect friction. Surface tension of soat solution =25 dyne cm−1. Take g=10ms−2
 View Solution
View Solution

