A uniform slender bar B of mass m and length L supported by a firctionless pivot at A is released from rest at its vertical position as shown the figure. Calculate the reaction at pivot when the bar just acquires the horizontal position shown dotted.

As there is no friction the mechanical energy will remain constant. Let us applying the conservation of mechanical energy between the vertuical position A and the horizontal position B.
Using △K+△U=0
(12IAω2−0)+(−mgL2)=0
which gives
ω=√3gL
Considering the free body diagram of the bar at this instant, the velocity of COM of bar at this instant is give below.
Let α be the angular acceleration of bar about A at the instant when it becomes horizontal.
α=τAIA=mgL2mL23=32gL
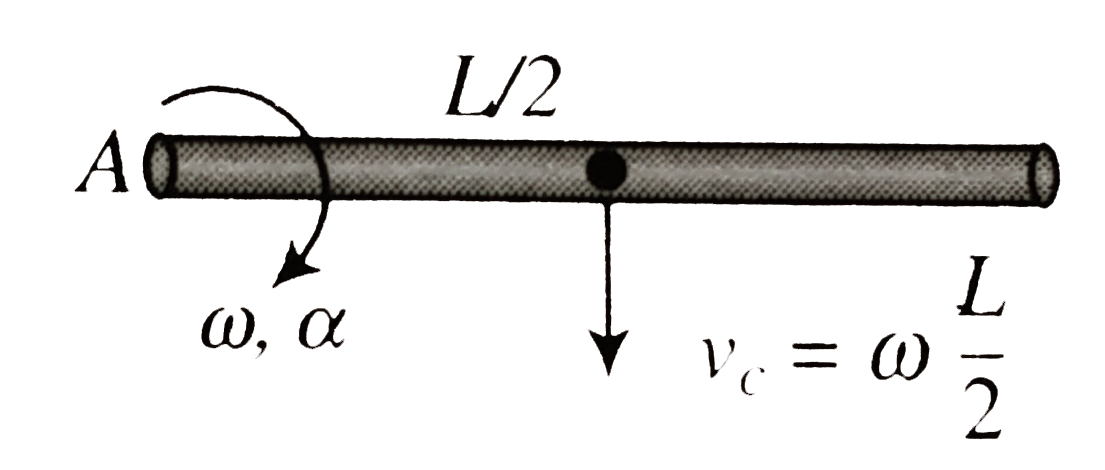
Let Nx and Ny are the components of reaction at A. Then in horizontal direction Nx=mar=mω2(L2) in vertical direction
andmg−Ny=mat .........i
at= acceleration of COM in y direction =(L2)a
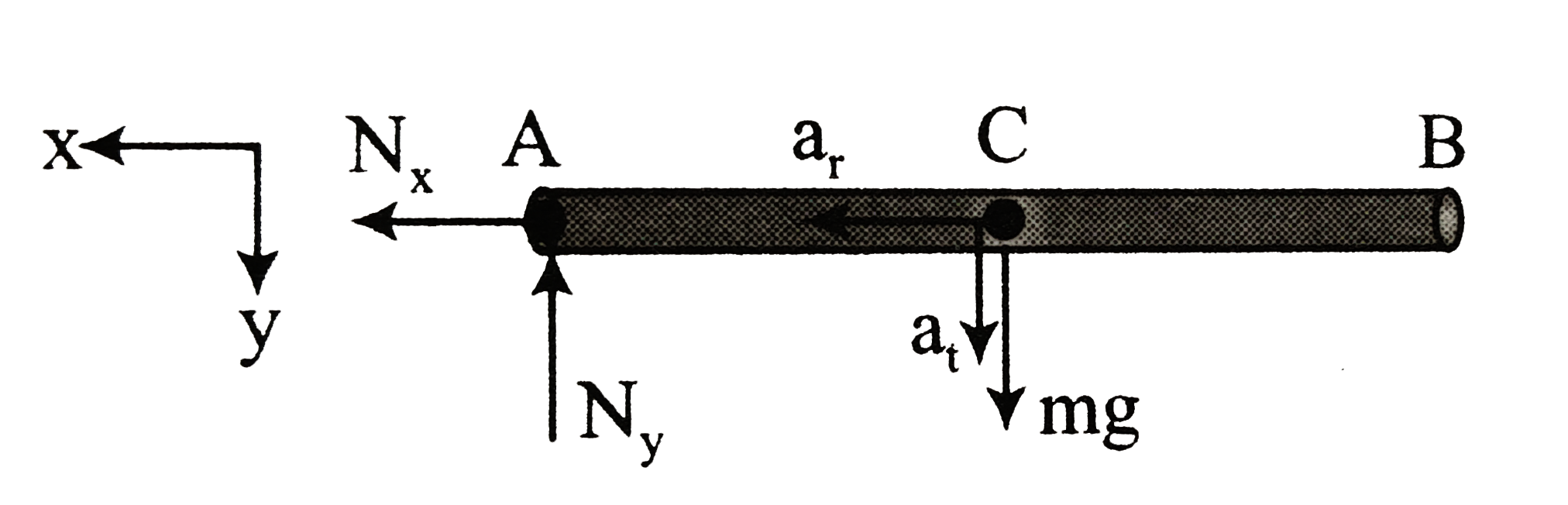
or Ny=mg−m(L2α)=mg−3mg4=mg4..........ii
Therefore, resultant reaction at support A is
N=√N2x+N2y
N=√(3mg2)2+(mg4)2=√374mg
tanα=NyNx=mg43mg2=16⇒α=tan−1(16)
Therefore, reaction at pivot is √374mg at an angle α=tan−1(16) with horizontal.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.2
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A slender rod of mass m and length L is pivoted about a horizontal axis through one end and released from rest at an angle of 30∘ above the horizontal. The force exerted by the pivot on the rod at the instant when the rod passes through a horizontal position is

View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is

View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View Solution
A thin plank of mass M and length l is pivoted at one end. The plank is releaed at 60∘ from the vertical. What is the magnitude and direction of the force on the pivot when the plank is horizontal?
View SolutionA simple pendulum A and a homogeneous rod B hinged at its enda are released from horizontal position as shown in figure.

View SolutionA small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is
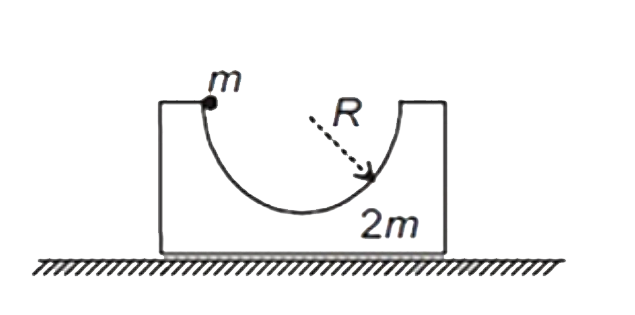
View SolutionA small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is

View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View Solution
