An inverted ice-cream cone is kept fixed on a frictionless surface with its base lying on the surface. A block kept on its slanted surface slides down with constant velocity, when the cone is cut along the along the slant surface of the cone and laid flat on the surface, it forms a semicircle the coefficient of friction on the surface of the cone is μ. then find the value of
The correct Answer is:3
To solve the problem step by step, we will analyze the forces acting on the block on the slanted surface of the cone and derive the expression for the coefficient of friction, μ.
Step 1: Understand the Geometry of the Cone
- We have an inverted ice-cream cone with a base radius r and height h.
- The block is sliding down the slanted surface of the cone at a constant velocity, which indicates that the net force acting on it is zero.
Step 2: Identify Forces Acting on the Block
- The forces acting on the block are:
- Gravitational force, mg (acting downwards).
- Normal force, N (acting perpendicular to the surface of the cone).
- Frictional force, f (acting up the slope, opposing the motion).
Step 3: Resolve the Gravitational Force
- The gravitational force can be resolved into two components:
- Parallel to the surface of the cone: mgsinθ
- Perpendicular to the surface of the cone: mgcosθ
Step 4: Apply Newton's Second Law
- Since the block slides down with constant velocity, the net force along the slope is zero:
mgsinθ=f
- The frictional force can be expressed as:
f=μN
- The normal force N is equal to the perpendicular component of the gravitational force:
N=mgcosθ
Step 5: Set Up the Equation
- Substituting the expression for N into the frictional force equation:
mgsinθ=μ(mgcosθ)
- Dividing both sides by mg (assuming m≠0):
sinθ=μcosθ
- Rearranging gives:
tanθ=μ
Step 6: Relate the Cone's Geometry to the Angle
- When the cone is cut along the slant surface and laid flat, it forms a semicircle with a radius R.
- The relationship between the radius of the cone and the height can be expressed as:
r=R2
- The angle θ can be determined from the geometry of the cone.
Step 7: Find the Angle θ
- From the geometry of the cone, we can find cosθ:
cosθ=rh
- Since r=R2 and h=R:
cosθ=R2R=12
- Therefore, θ=60∘.
Step 8: Calculate μ
- Using the relationship tanθ=μ:
tan60∘=√3
- Thus, μ=√3.
Step 9: Find μ2
- Finally, we need to find μ2:
μ2=(√3)2=3
Final Answer
The value of μ2 is 3.
---
- We have an inverted ice-cream cone with a base radius r and height h.
- The block is sliding down the slanted surface of the cone at a constant velocity, which indicates that the net force acting on it is zero.
- The forces acting on the block are:
- Gravitational force, mg (acting downwards).
- Normal force, N (acting perpendicular to the surface of the cone).
- Frictional force, f (acting up the slope, opposing the motion).
- The gravitational force can be resolved into two components:
- Parallel to the surface of the cone: mgsinθ
- Perpendicular to the surface of the cone: mgcosθ
- Since the block slides down with constant velocity, the net force along the slope is zero:
mgsinθ=f
- The frictional force can be expressed as:
f=μN
- The normal force N is equal to the perpendicular component of the gravitational force:
N=mgcosθ
- Substituting the expression for N into the frictional force equation:
mgsinθ=μ(mgcosθ)
- Dividing both sides by mg (assuming m≠0):
sinθ=μcosθ
- Rearranging gives:
tanθ=μ
- When the cone is cut along the slant surface and laid flat, it forms a semicircle with a radius R.
- The relationship between the radius of the cone and the height can be expressed as:
r=R2
- The angle θ can be determined from the geometry of the cone.
- From the geometry of the cone, we can find cosθ:
cosθ=rh
- Since r=R2 and h=R:
cosθ=R2R=12
- Therefore, θ=60∘.
- Using the relationship tanθ=μ:
tan60∘=√3
- Thus, μ=√3.
- Finally, we need to find μ2:
μ2=(√3)2=3
The value of μ2 is 3.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.7220videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.711videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.709videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
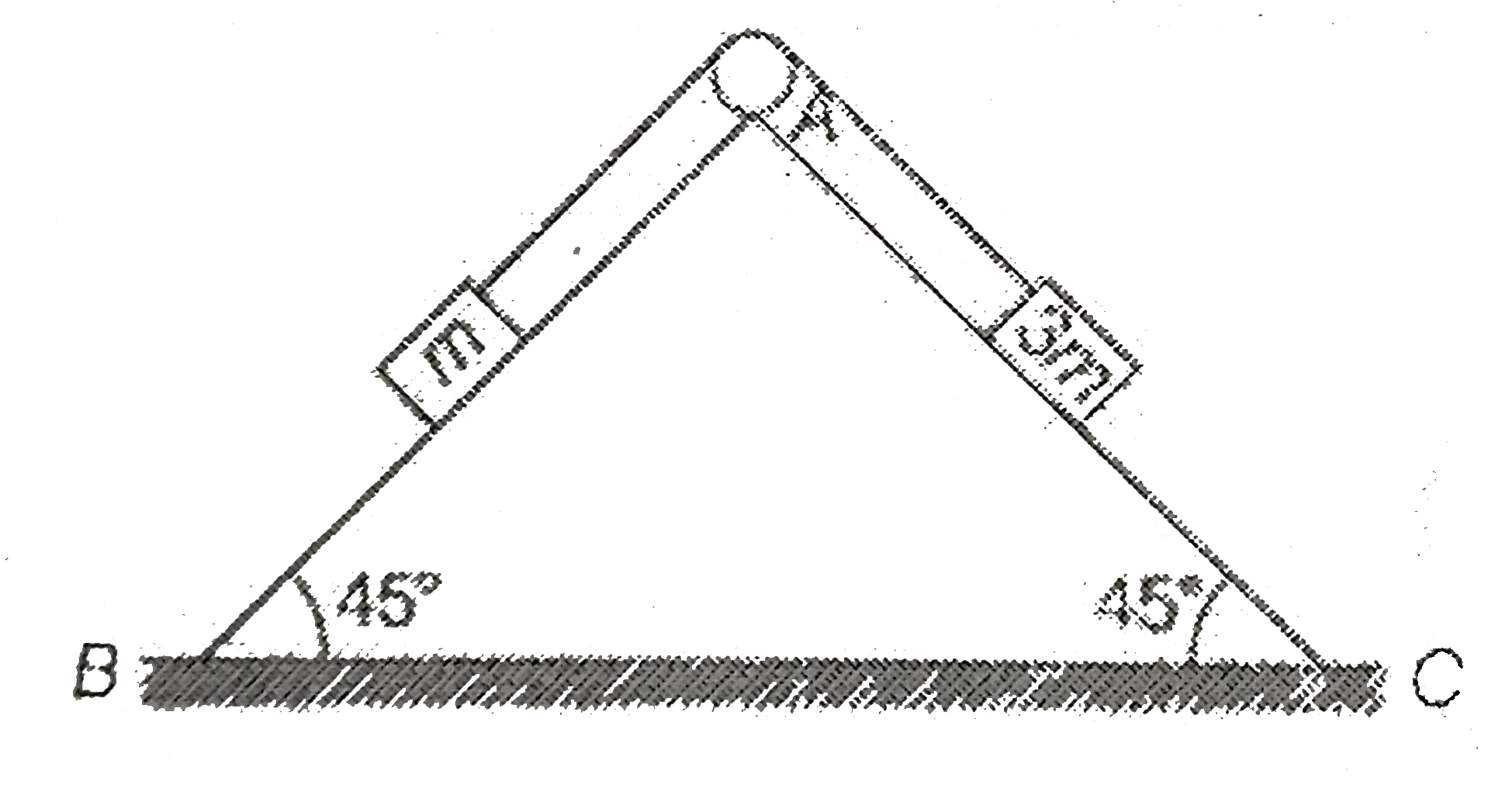
In the given figurethe wedge is fixed, pulley is frictionless and string is light. Surface AB is frictionless whereas AC is rough. If the block of mass 3m. Slides down. With conttant velocity, then the coefficient of friction between surface AC and the block is
 View Solution
View SolutionThe lateral surface of a cylinder is equal to the curved surface of a come. If the radius be the same, find the ratio of the height of the cylinder and slant height of the cone.
View SolutionThe lateral surface of a cylinder is equal to the curved surface of a come. If the radius be the same, find the ratio of the height of the cylinder and slant height of the cone.
View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View SolutionA rectangular wooden box 10cm×20cm×40cm is size is kept on a horizontal surface with its of lergest are on the surface .A minimum force of 10N applied are on the surface sets the box in sliding motion along the surface If the surface, minimum force applied parallel to the surface , to set the box in motion , is
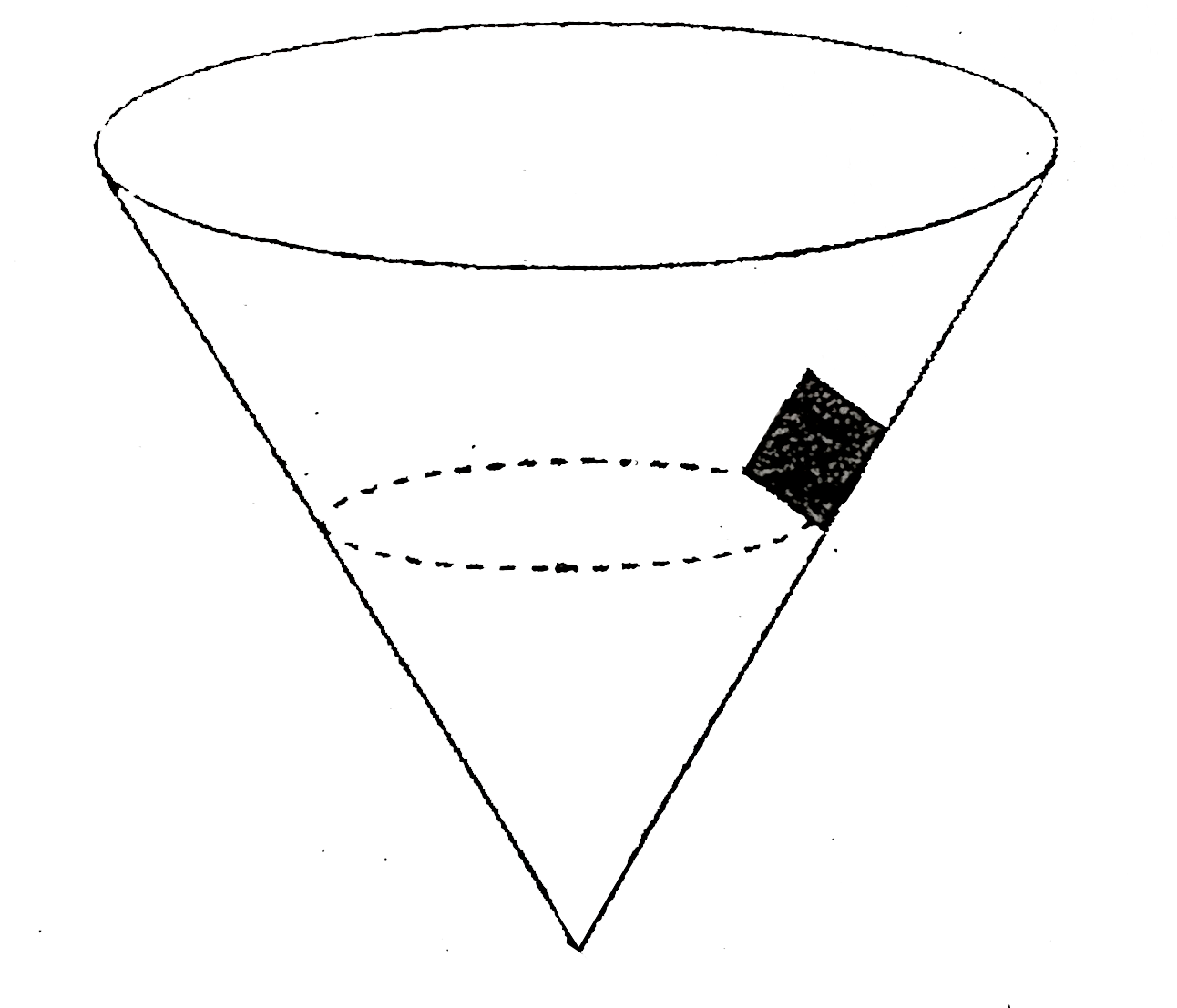
View SolutionConsider a block moving in a horizontal circular path on the inner surface of a cone. The normal force on the block is :
 View Solution
View SolutionThe height of a cone is 16 cm and its base radius is 12 cm. Find the curved surface area and the total surface area of the cone
View SolutionThe area of the curved surface of a cone is 60π cm2. If the slant height of the cone be 8cm, find the radius of the base.
View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If mu is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:
 View Solution
View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:
 View Solution
View Solution

