One stone is projected horizontally from a 20m high cliff with an initial speed of 10ms−1. A second stone is simultaneously dropped from that cliff. Which of the following is true?
Both strike the ground with same speed.
Tha ball with initial speed 10ms−1 reaches the ground first.
The ball which is dropped, reaches the ground first.
Both strike the ground with different speed
The correct Answer is:D
To solve the problem, we need to analyze the motion of both stones: one that is projected horizontally and the other that is dropped vertically.
1. Identify the given data:
- Height of the cliff (h) = 20 m
- Initial speed of the horizontally projected stone (u₁) = 10 m/s
- Initial speed of the dropped stone (u₂) = 0 m/s (since it is dropped)
2. Determine the time taken for both stones to reach the ground:
- For the stone that is dropped (second stone), we can use the equation of motion:
s=ut+12at2
Here, s=−h=−20m, u=0, and a=g≈9.81m/s2 (acceleration due to gravity).
−20=0⋅t2+12(−g)t22
This simplifies to:
−20=−12gt22
Rearranging gives:
t22=40g
Thus:
t2=√40g
3. For the stone that is projected horizontally (first stone):
- The vertical motion is the same as that of the dropped stone because both stones fall the same vertical distance under the influence of gravity. Therefore, we can use the same equation:
−20=0⋅t1+12(−g)t21
This gives:
t21=40g
Thus:
t1=√40g
4. Compare the times:
- Since both t1 and t2 are equal:
t1=t2
- Therefore, both stones hit the ground at the same time.
5. Determine the speeds at which they hit the ground:
- The speed of the dropped stone just before it hits the ground can be calculated using:
v=u+gt
For the dropped stone:
v2=0+gt2=g√40g=√40g
- The speed of the horizontally projected stone just before it hits the ground can be calculated using:
v=u+gt
For the horizontally projected stone:
v1=10+gt1=10+g√40g=10+√40g
6. Conclusion:
- Both stones strike the ground at the same time, but with different speeds.
Final Answer:
Both stones strike the ground at the same time, but they do not have the same speed.
- Height of the cliff (h) = 20 m
- Initial speed of the horizontally projected stone (u₁) = 10 m/s
- Initial speed of the dropped stone (u₂) = 0 m/s (since it is dropped)
- For the stone that is dropped (second stone), we can use the equation of motion:
s=ut+12at2
Here, s=−h=−20m, u=0, and a=g≈9.81m/s2 (acceleration due to gravity).
−20=0⋅t2+12(−g)t22
This simplifies to:
−20=−12gt22
Rearranging gives:
t22=40g
Thus:
t2=√40g
- The vertical motion is the same as that of the dropped stone because both stones fall the same vertical distance under the influence of gravity. Therefore, we can use the same equation:
−20=0⋅t1+12(−g)t21
This gives:
t21=40g
Thus:
t1=√40g
- Since both t1 and t2 are equal:
t1=t2
- Therefore, both stones hit the ground at the same time.
- The speed of the dropped stone just before it hits the ground can be calculated using:
v=u+gt
For the dropped stone:
v2=0+gt2=g√40g=√40g
- The speed of the horizontally projected stone just before it hits the ground can be calculated using:
v=u+gt
For the horizontally projected stone:
v1=10+gt1=10+g√40g=10+√40g
- Both stones strike the ground at the same time, but with different speeds.
Both stones strike the ground at the same time, but they do not have the same speed.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15ms−1 and 30ms−1 respectively. The time variation of the relative position of the second stone with respect to the first is shown in the figure. The equation of the linear part is
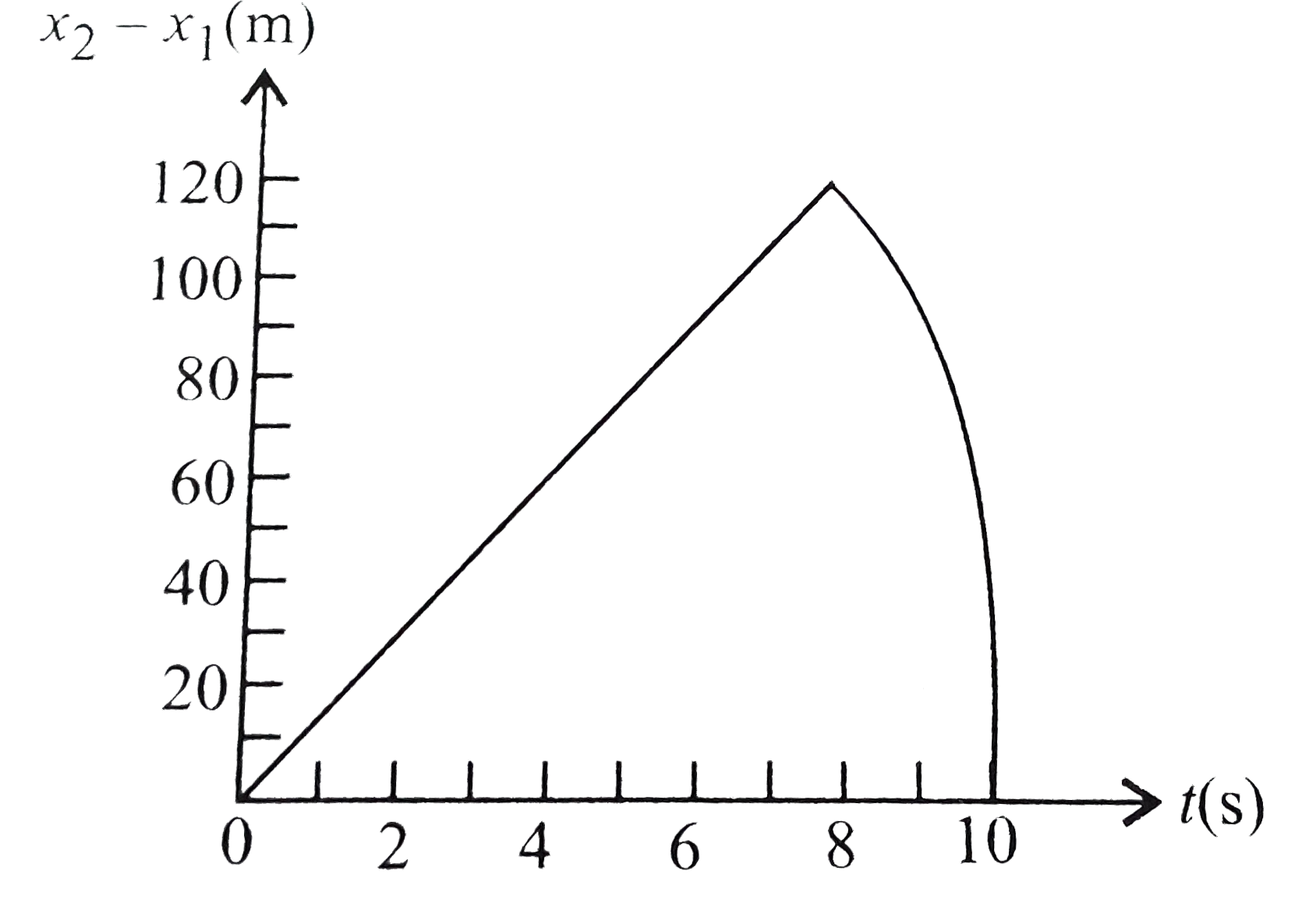 Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20t
Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20t - Question 2 - Select One
From the top of a 490 m high cliff, a boy throws a stone horizontally with a initial speed of 15ms−1. What is the time taken by the stone to reach the ground.
A5 sB10 sC12 sD15 s
A ball is projected downward from the top of a cliff of height h with an initial speed v.Another ball is simultaneously projected vertically up from the bottommost of the cliff with the same speed.When do they meet?
View SolutionOn the earth, a stone is thrown from a height in a direction parallel to the earth's surfaces while another stone is simultaneously dropped from the same height. Which stone whould reach the ground first and why ?
View SolutionTwo stones AandB are projected simultaneously from the top of a 100−m high tower. Stone B is projected horizontally with speed 10ms−1, and stone A is droppd from the tower. Find out the following :
(a) Time of flight of the two stone
(b) Distance between two stones after 3s
(c ) Angle of strike with ground
(d) Horizontal range of particle B.View SolutionTwo stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
View SolutionA stone A is dropped from rest from a height h above the ground.A second stone B is simultaneously thrown vertically up from a point on the ground with velocity v.The line of motion of both the stones is same .Find if the value of v which would enable the stone B to meet the stone A midway between their initial positions =
 View Solution
View SolutionA stone is projected at angle of tan−1(3/4) to the horizontal with a speed of 30ms−1. Find its position after 2 seconds. g=10ms−1 ?
View Solution

