An eaeroplane is to go along straight line from A to B, and back again. The relative speed with respect to wind is V. The wind blows perpendicular to line AB with speed v. The distance between A and B is . The total time for the round trip is:
The correct Answer is:A
To solve the problem, we need to determine the total time taken for an airplane to travel from point A to point B and back again, considering the effects of wind. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have an airplane flying from point A to point B and back. The distance between A and B is l, the speed of the airplane relative to the wind is V, and the wind blows perpendicular to the line AB with speed v.
Step 2: Analyze the Motion
When the airplane is flying, its velocity can be broken down into two components:
- A horizontal component (along the line AB): Vcosθ
- A vertical component (against or with the wind): Vsinθ
Step 3: Relate the Vertical Component to Wind Speed
Since the wind blows perpendicular to the path of the airplane, we can set the vertical component of the airplane's speed equal to the wind speed:
Vsinθ=v
From this, we can express sinθ:
sinθ=vV
Step 4: Use the Pythagorean Identity
We know from trigonometry that:
sin2θ+cos2θ=1
Substituting for sinθ:
(vV)2+cos2θ=1
This leads us to find cosθ:
cos2θ=1−(vV)2
cosθ=√1−v2V2=√V2−v2V
Step 5: Calculate the Effective Speed
The effective speed of the airplane in the horizontal direction (along AB) is:
Vcosθ=V⋅√V2−v2V=√V2−v2
Step 6: Calculate the Total Distance
The total distance for the round trip is:
Total Distance=l+l=2l
Step 7: Calculate the Total Time
The total time T for the round trip can be calculated using the formula:
T=Total DistanceEffective Speed=2l√V2−v2
Final Answer
Thus, the total time for the round trip is:
T=2l√V2−v2
---
We have an airplane flying from point A to point B and back. The distance between A and B is l, the speed of the airplane relative to the wind is V, and the wind blows perpendicular to the line AB with speed v.
When the airplane is flying, its velocity can be broken down into two components:
- A horizontal component (along the line AB): Vcosθ
- A vertical component (against or with the wind): Vsinθ
Since the wind blows perpendicular to the path of the airplane, we can set the vertical component of the airplane's speed equal to the wind speed:
Vsinθ=v
From this, we can express sinθ:
sinθ=vV
We know from trigonometry that:
sin2θ+cos2θ=1
Substituting for sinθ:
(vV)2+cos2θ=1
This leads us to find cosθ:
cos2θ=1−(vV)2
cosθ=√1−v2V2=√V2−v2V
The effective speed of the airplane in the horizontal direction (along AB) is:
Vcosθ=V⋅√V2−v2V=√V2−v2
The total distance for the round trip is:
Total Distance=l+l=2l
The total time T for the round trip can be calculated using the formula:
T=Total DistanceEffective Speed=2l√V2−v2
Thus, the total time for the round trip is:
T=2l√V2−v2
Topper's Solved these Questions
Similar Questions
An aeroplane flies along a straight path AandB and returns back again. The distance between AandB is l and the aeroplane maintains the constant speed v w.r.t. wind.
There is a steady wind with a speed u at an angle θ with line AB. Determine the expression for the total time of the trip.
 .View Solution
.View SolutionAn airplane flies northward from town A and B and then back again. There is a steady wind blowing towards the north so that for the first state of the trip, the airplane is flying in the same direction as the wind and for the return trip of the journey, the airplane is flying opposite of the wind. The total trip time Tω as compared to the total trip time in the absence of any winds T0 is:
View SolutionA body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph:
View SolutionA straight wire of length L is bent into a semicircle. It is moved in a uniform magnetic field with speed v with diameter perpendicular to the field. The induced emf between the ends of the wire is
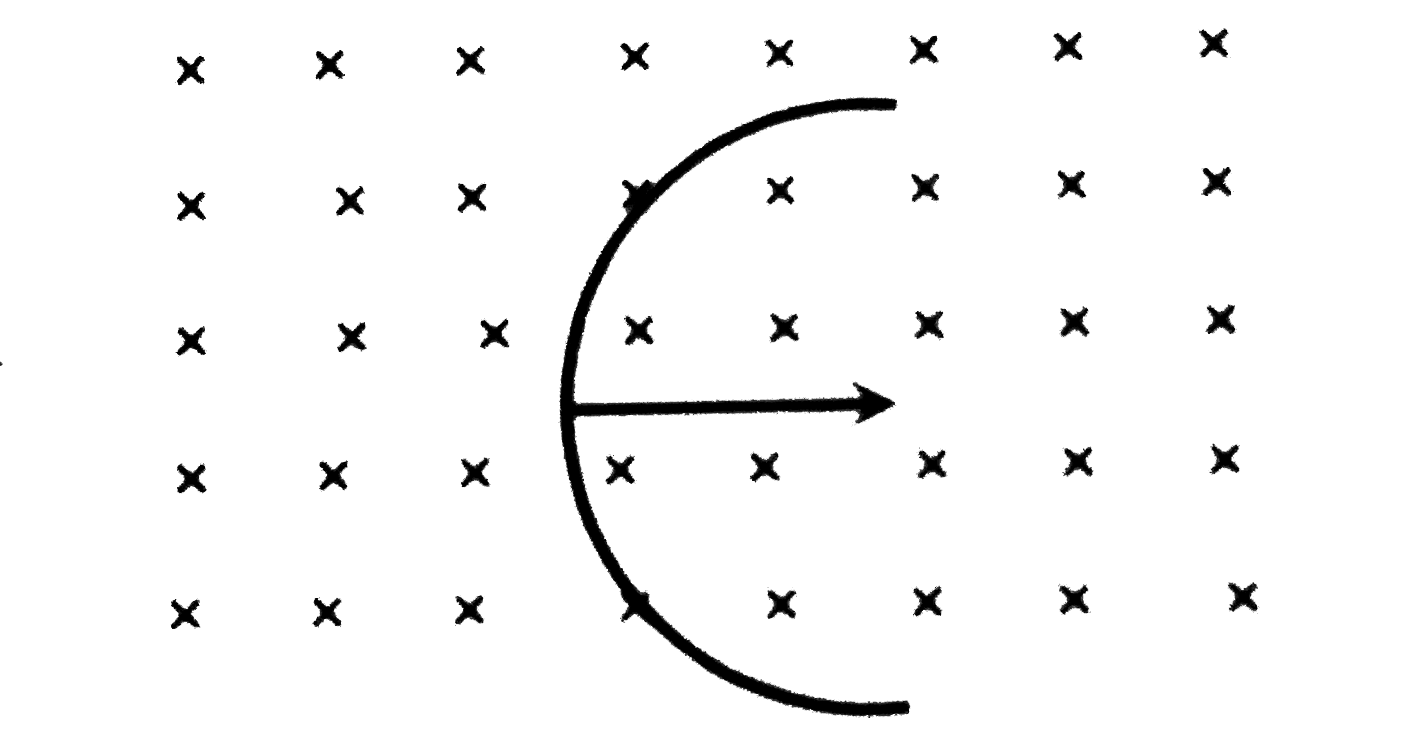 View Solution
View SolutionA man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
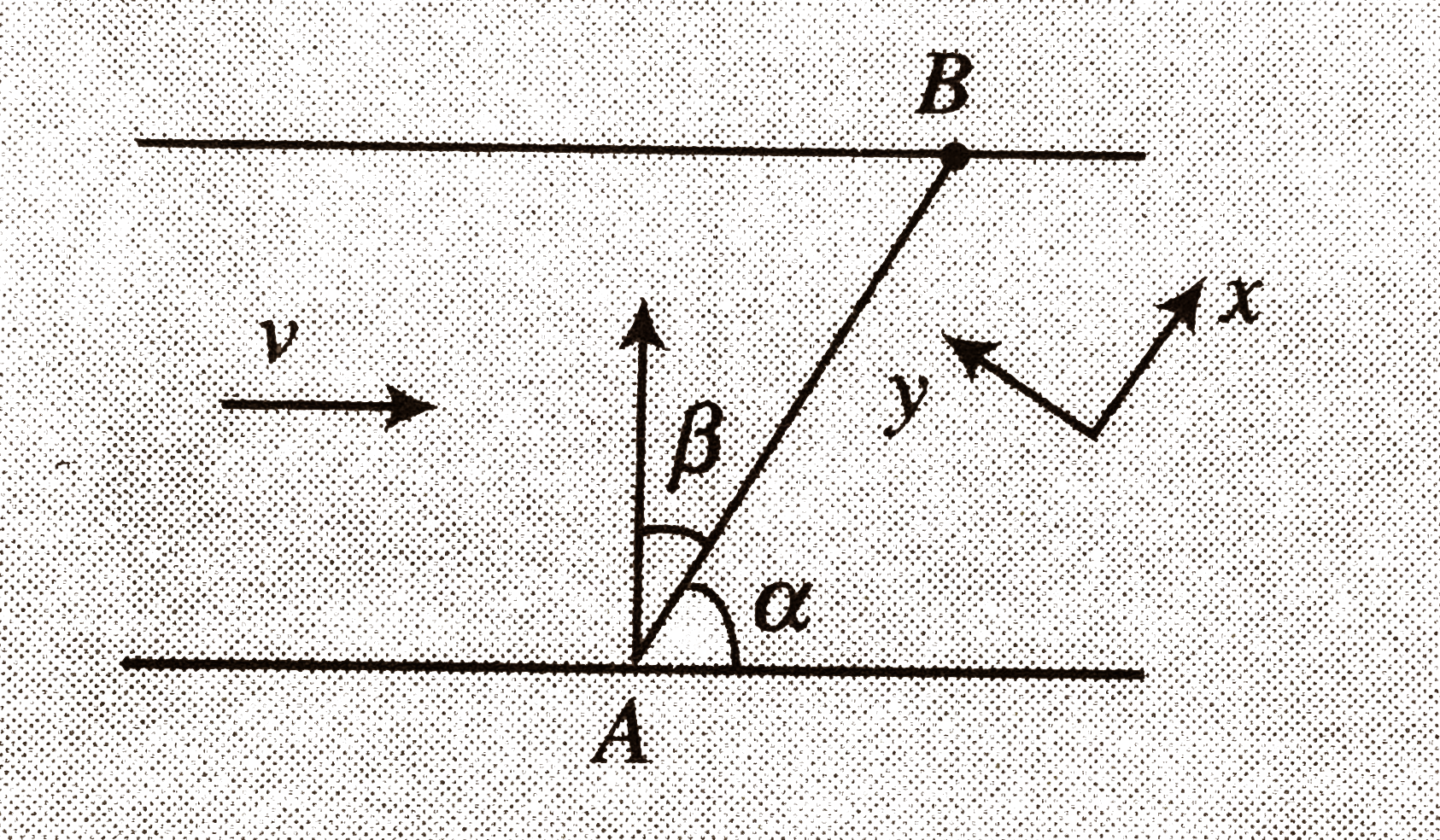 .View Solution
.View SolutionThe distance between two moving particles P and Q at any time is a.If vr be their relative velocity and if u and v be the components of vr, along and perpendicular to PQ.The closest distance between P and Q and time that elapses before they arrive at their nearest distance is
View SolutionA particle travels along a straight line. It covers halg the distance with a speed (v). The remaining part of the distance was covere with speed v1 for half the time and with speed v2 for the other half the time . Find the average speed of the particle over the entire motion.
View SolutionA particle moving with uniform acceleration from A to B along a straight line has velcities v1 and v2 at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C .
 .View Solution
.View SolutionA point moves in a straight line under the retardation av2, where 'a' is a positive constant and v is speed. If the initial speed is u, the distance covered in 't' seconds is :
View SolutionA particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle with respect to origin O is LA when it is at A and LB when it is at B, then
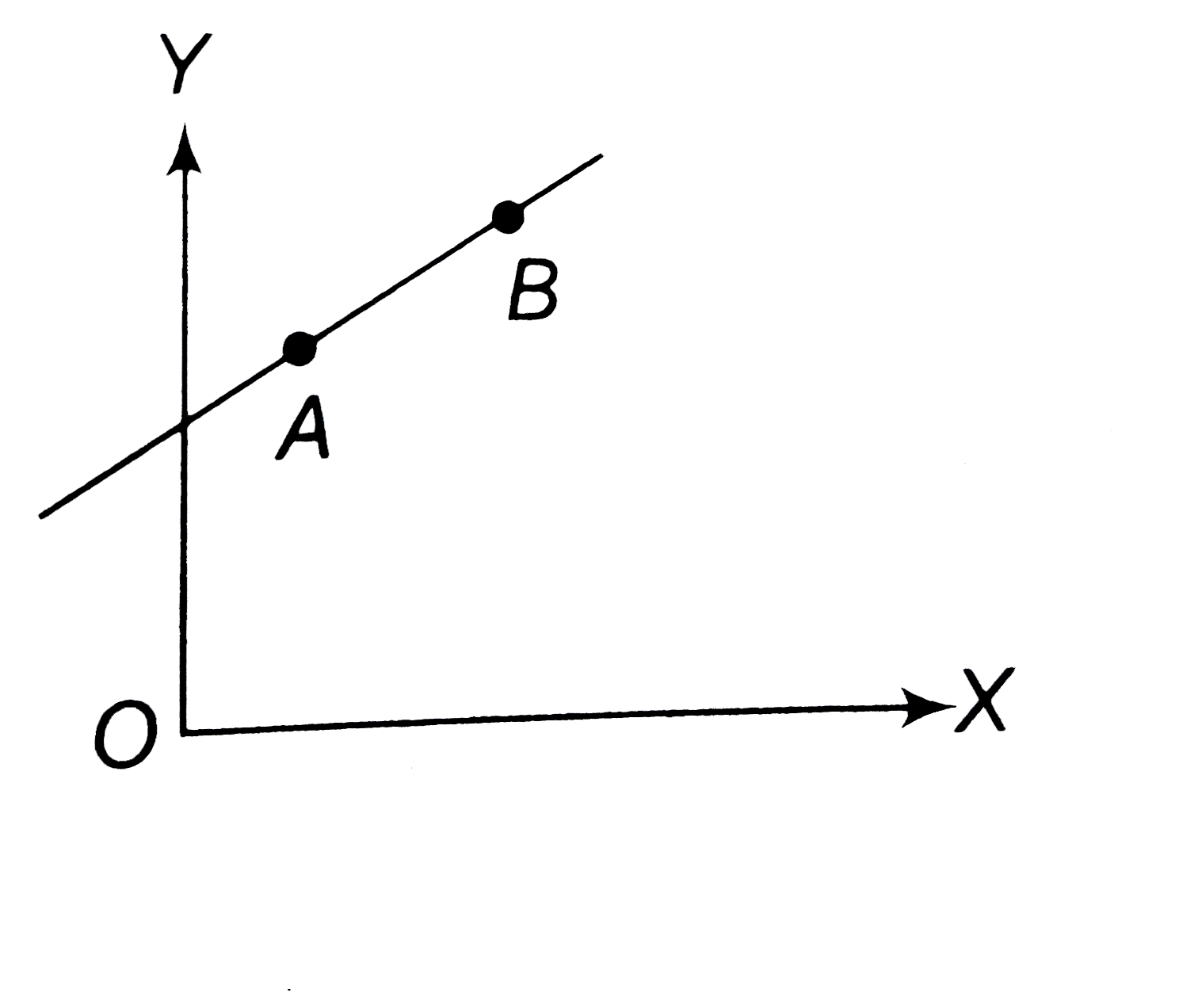 View Solution
View Solution

