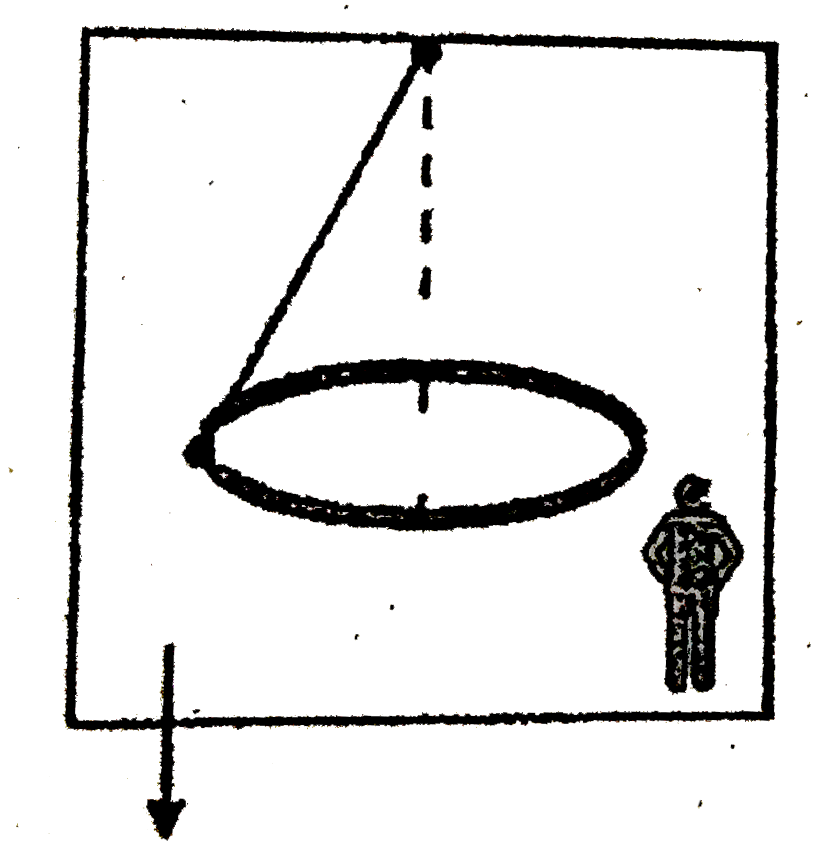
In the figure shown a lift goes downwards with a constant retardation. An observer in the lift observers a conical pendulam in the lift, revolving in a horizontal circle with time period 2 seconds. The distance between the centre of the circle and the point of suspension is 2.0 m. the retardation of the lift in m/s2 is
1m/s2
2m/s2
3m/s2
4m/s2
The correct Answer is:A
T=2π√lcosθgeff=2π√hgeff
geff=g+a, put T=2 ⇒a=10m/s2 Retardation 10m/s2
Topper's Solved these Questions
Similar Questions
A lift starts from rest with a constant upward acceleration It moves 1.5 m in the first 0.4 A person standing in the lift holds a packet of 2 kg by a string Calculate the tension in the string during the motion .
View SolutionThe mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
View SolutionA a certain instant of time a ballon is moving downwards with speed of 5m/s. It has a constant retardation of 5m/s2. A man in the ballon drops a stone at that instant. It hits the ground after 2s. Then the speed with which the stone hits the ground is.
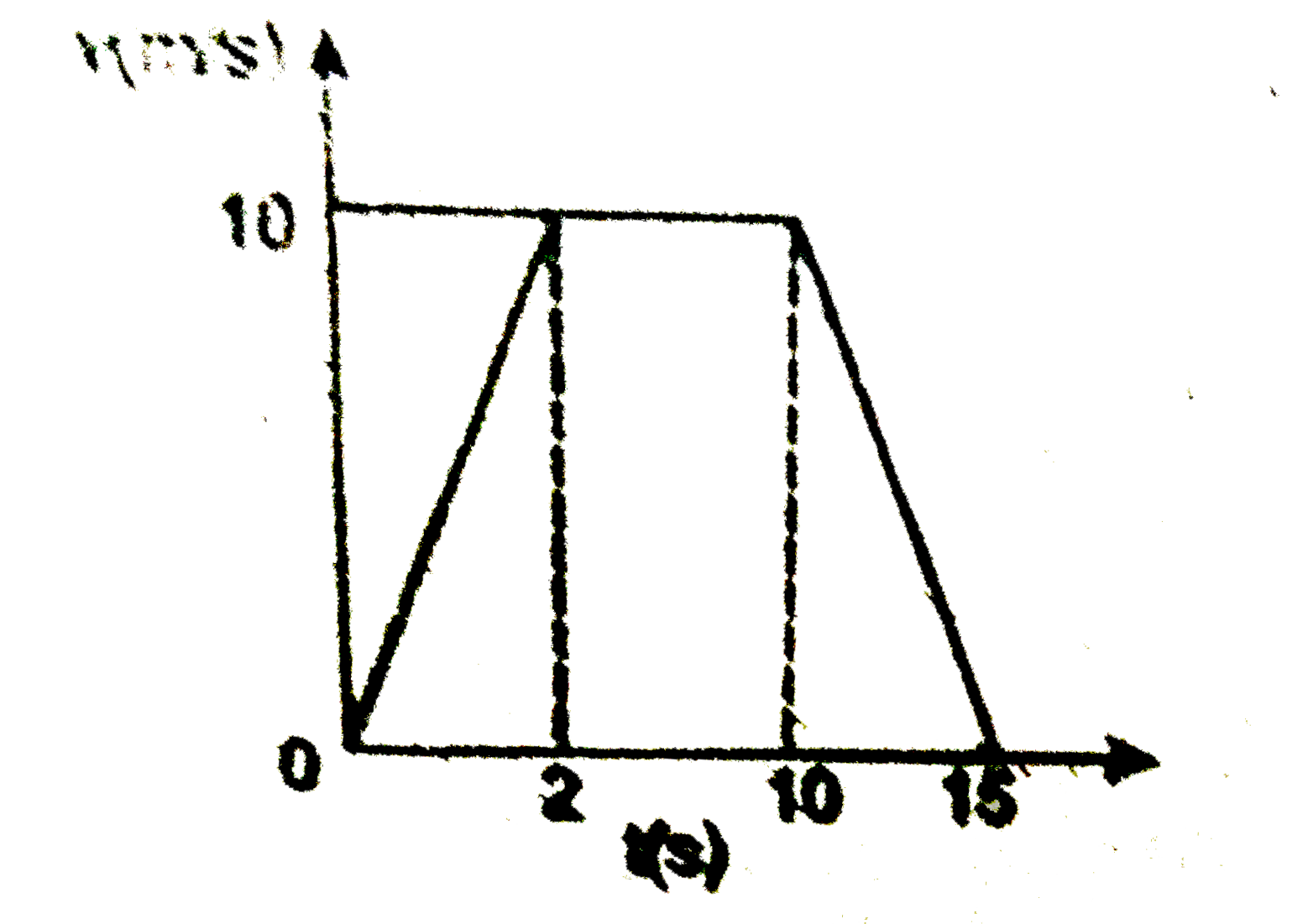
View SolutionA lift of mass 1000 kg is going up. The variation in the speed of lift is shown in figure. Then the minimum tension in the rope will be (g=10m/s2)
 View Solution
View SolutionA lift accelerates downwards from rest at rate of 2m/s2, starting 100m above the ground. After 3 sec, an object falls out of the lift. Which will reach the ground first? What is the time interval between their striking the ground?
View Solution
A lift is moving upwards with a constant speed of 5ms. The speed of one of the pulleys is 5ms as shown. Then the speed of second pulley is:View SolutionA body is thrown up in a lift with a velocity 5ms−1 relative to the lift and the time of flight is found to be 0.8 s. The acceleration with which the lift is moving up is (g=10ms−2)
View SolutionA lift performs the first part of its ascent with uniform acceleration a and the remaining with uniform retardation 2a. If t is the time of ascent, find the depth of the shaft.
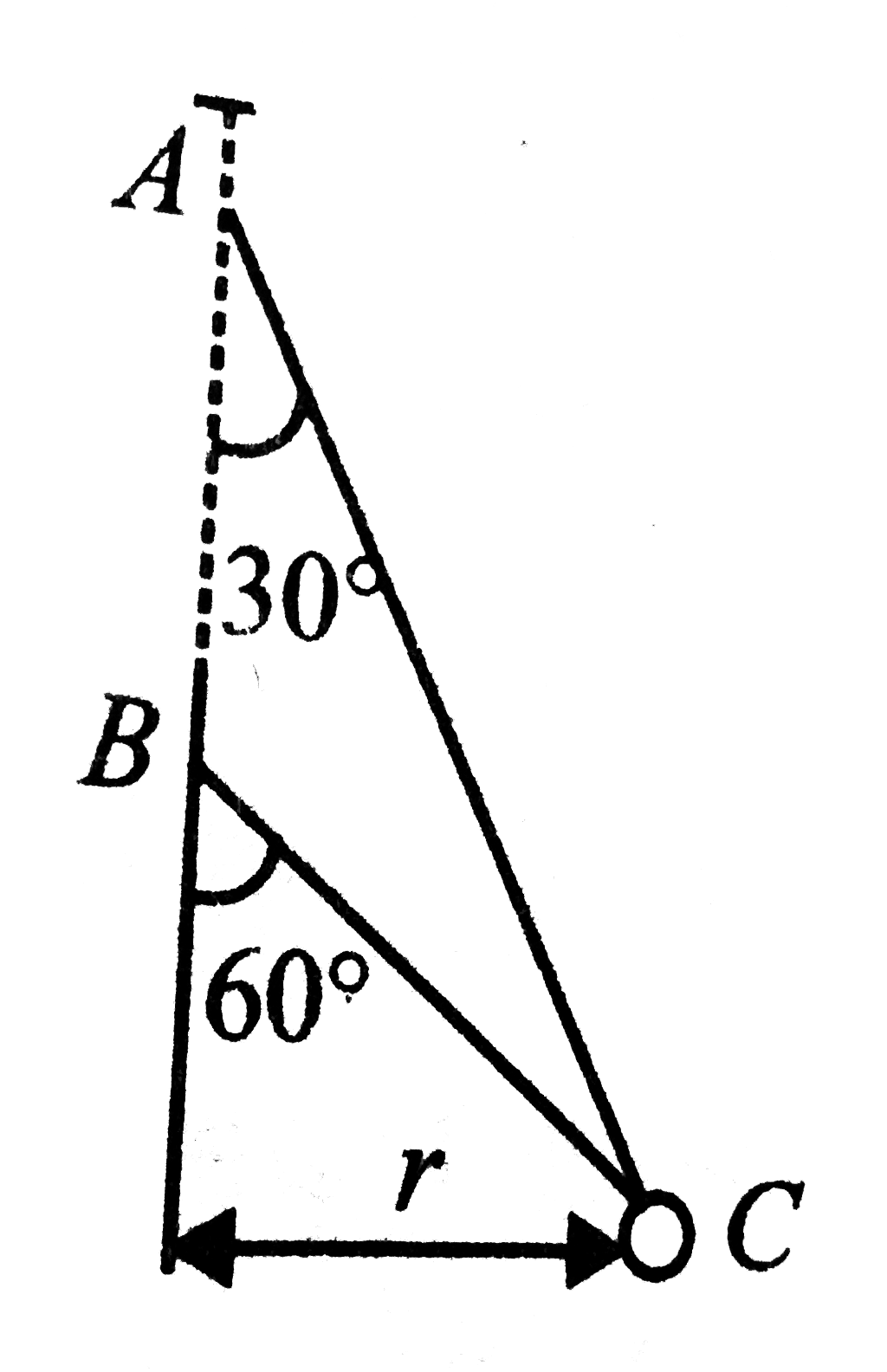
View SolutionA single wire ACB passes through a smooth ring at C when revolves at a constant speed in the horizontal circle of radius r=6.4m as shown in the figure. Find the speed (in m/s) of revolution of the ring.
 View Solution
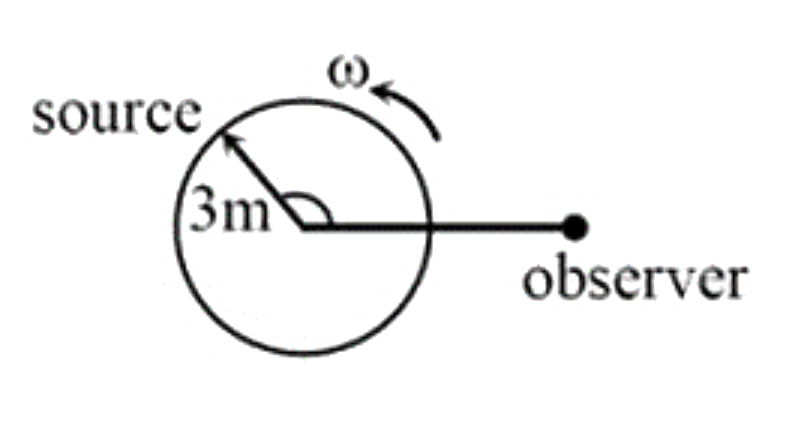
View SolutionA source is moving on a circle of radius 3m with constant angular velocity ω=5rads−1. If the observer is at a distnace 5 cm from the centre of the circle, the time interval between the maximum and minimum frequency recived by the observer is
 View Solution
View Solution

