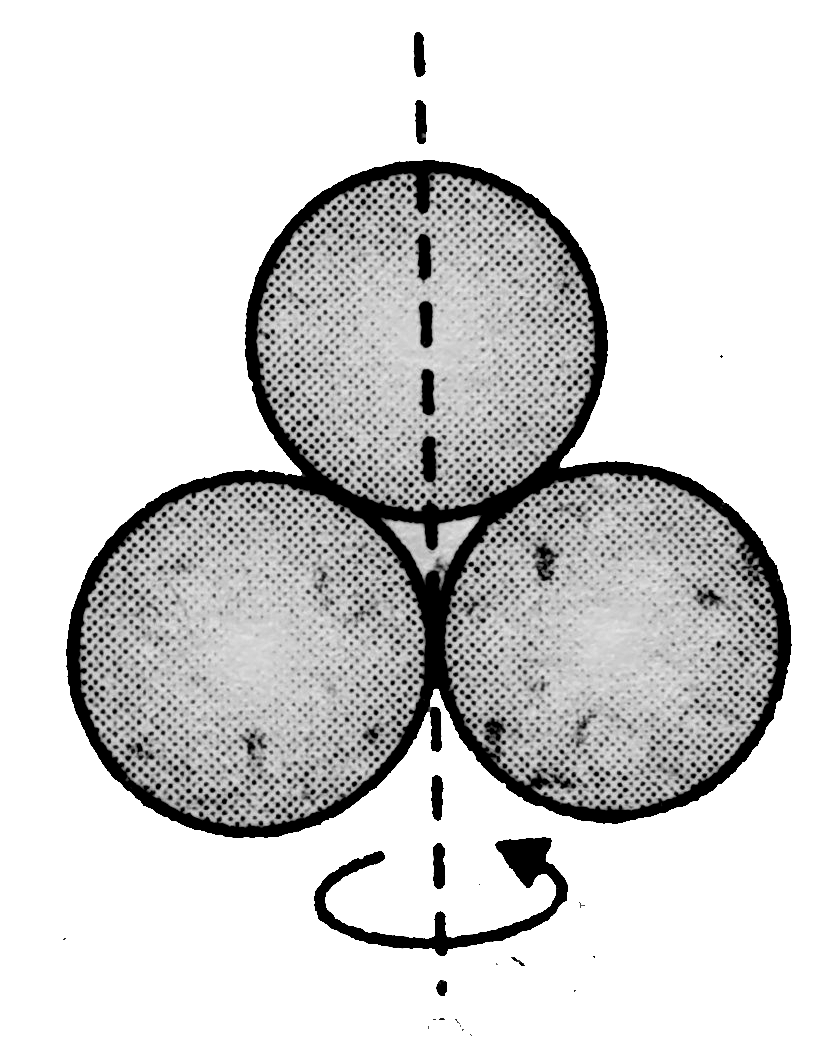
Three rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
√65r
√56r
√67r
√76r
The correct Answer is:D
I=I1+I2+I3
I1=I2=32mr2
I3=mr22
∴I=I1+I2+I3=72mr2
moment of inertia=3mk4 where k is radius of gyration
3mk2=72mr2
⇒k=√76r
Topper's Solved these Questions
Similar Questions
Three rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
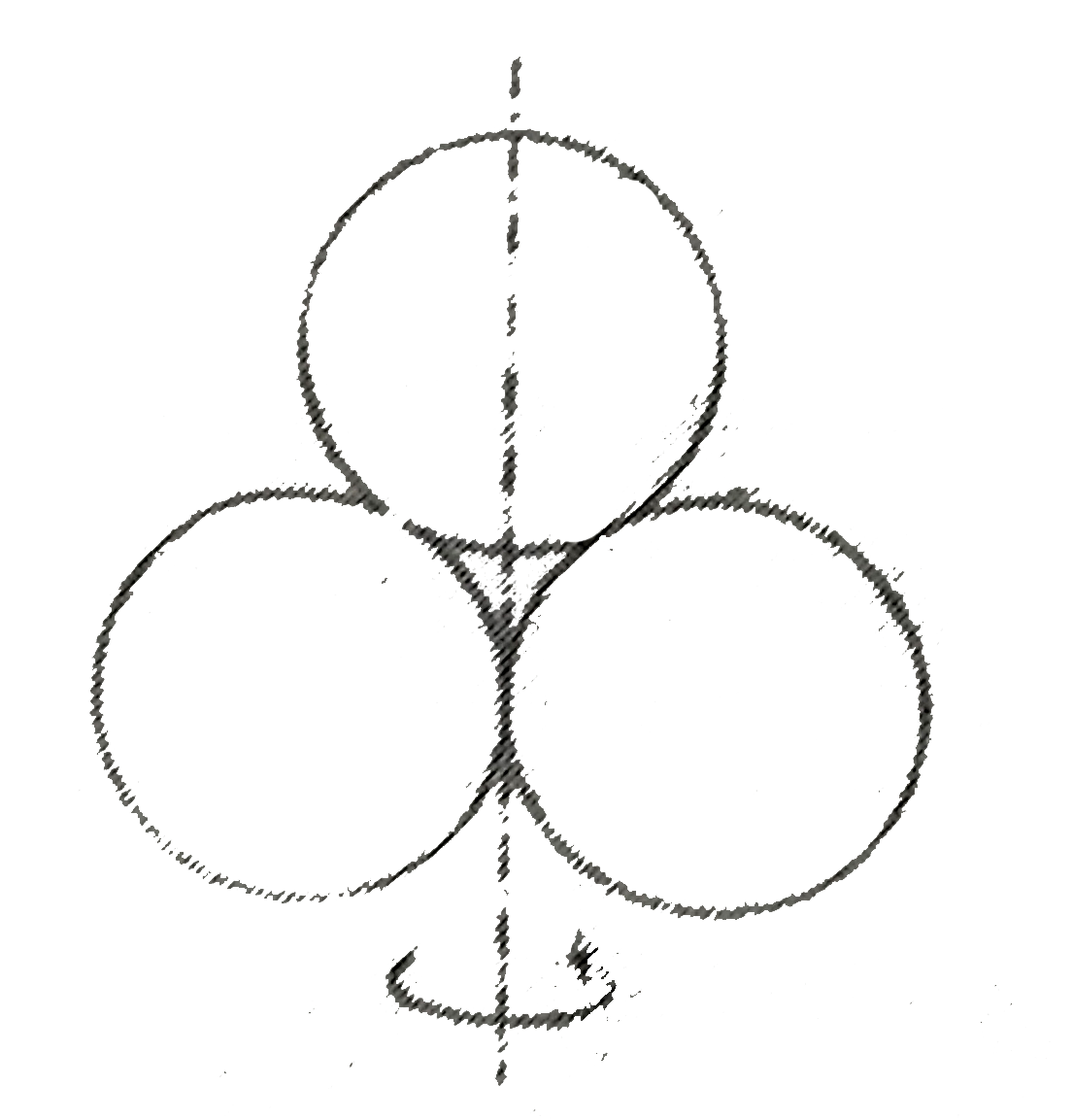 View Solution
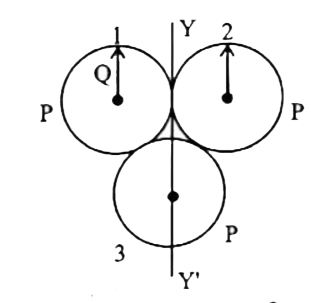
View SolutionThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
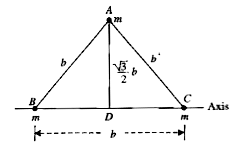 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2
Three rings each of mass M and radius R are arranged according to the figure. The moment of inertia of this system about an axis XX' on its plane would be
 View Solution
View SolutionFour rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be
 View Solution
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View SolutionTwo masses m1andm2 are placed at a distance r from each other. Find out the moment of inertia of system about an axis passing through their centre of mass.
View SolutionThree identical rings of masses m each and radius r are kept in contact as shown in Fig. Find the moment of inertia of the system about a common tangent.
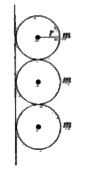 View Solution
View SolutionThree identical rods each of mass M, length l are joined to form an equilateral ΔABC . Find the Moment of Inertia about BC as shown.
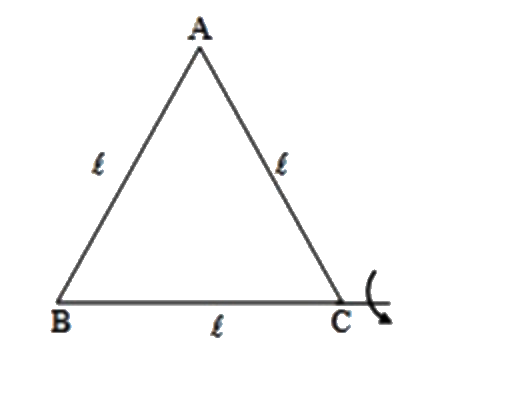 View Solution
View SolutionSeven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is :
 View Solution
View Solution

