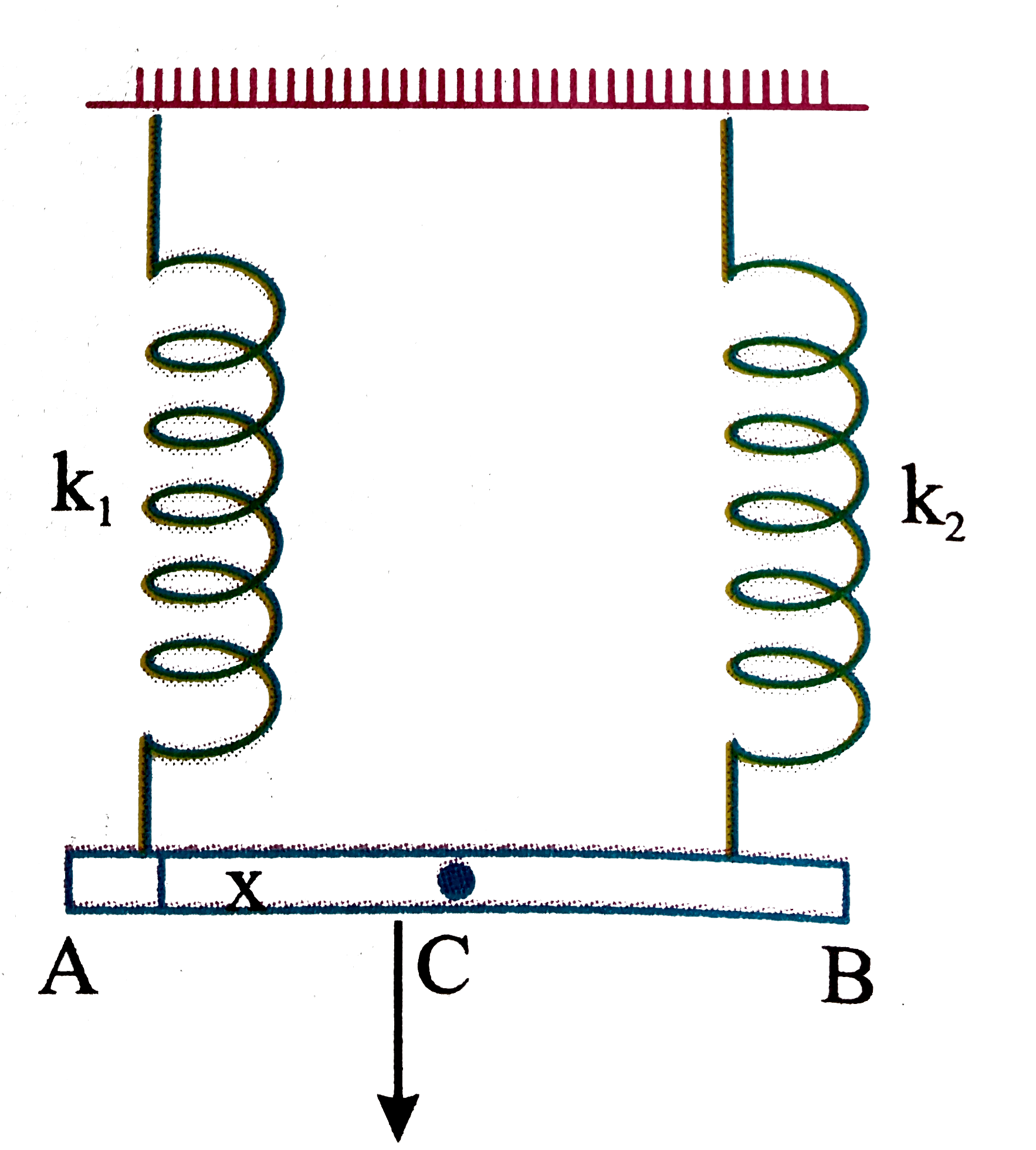
Two light vertical springs with equal natural length and spring constants k1 and k2 are separated by a distance l. Their upper ends are rigidly connected and the lower ends are connected to A and B of a light horizontal rod AB. A vertically downwards force F is applied at point C on the rod. AB will remain horizontal in equilibrium if the distance AC is
l2
lk1k2+k1
lk2k1
lk2k1+k2
The correct Answer is:D
AC=x
x0=ext0. In each spring
Torque about C
K1x0x=K2x0(l−x)
x=lk2k1+k2
Topper's Solved these Questions
Similar Questions
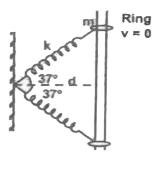
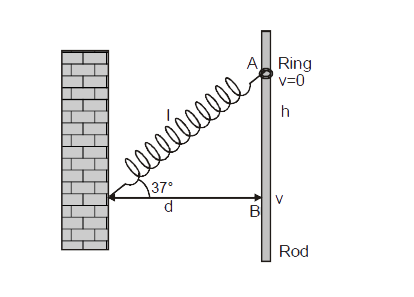
One end a light spring of natural length d and spring constant k(=mg/d) is fixed on a rigid support and the other end is fixed to a smoth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the support. Initially , the spring makes an angle of 37∘ with the horizontal as shown in the figure. The system is released from rest. The speed of the ring at the same angle subtended downward will be
 View Solution
View SolutionTwo particles connected by a rigid light rod AB, lying on a smooth horizontal table. An impulse J is applied at A in the plane of thetable and perpendicular at AB. Then the velocity of particle at A is
View Solution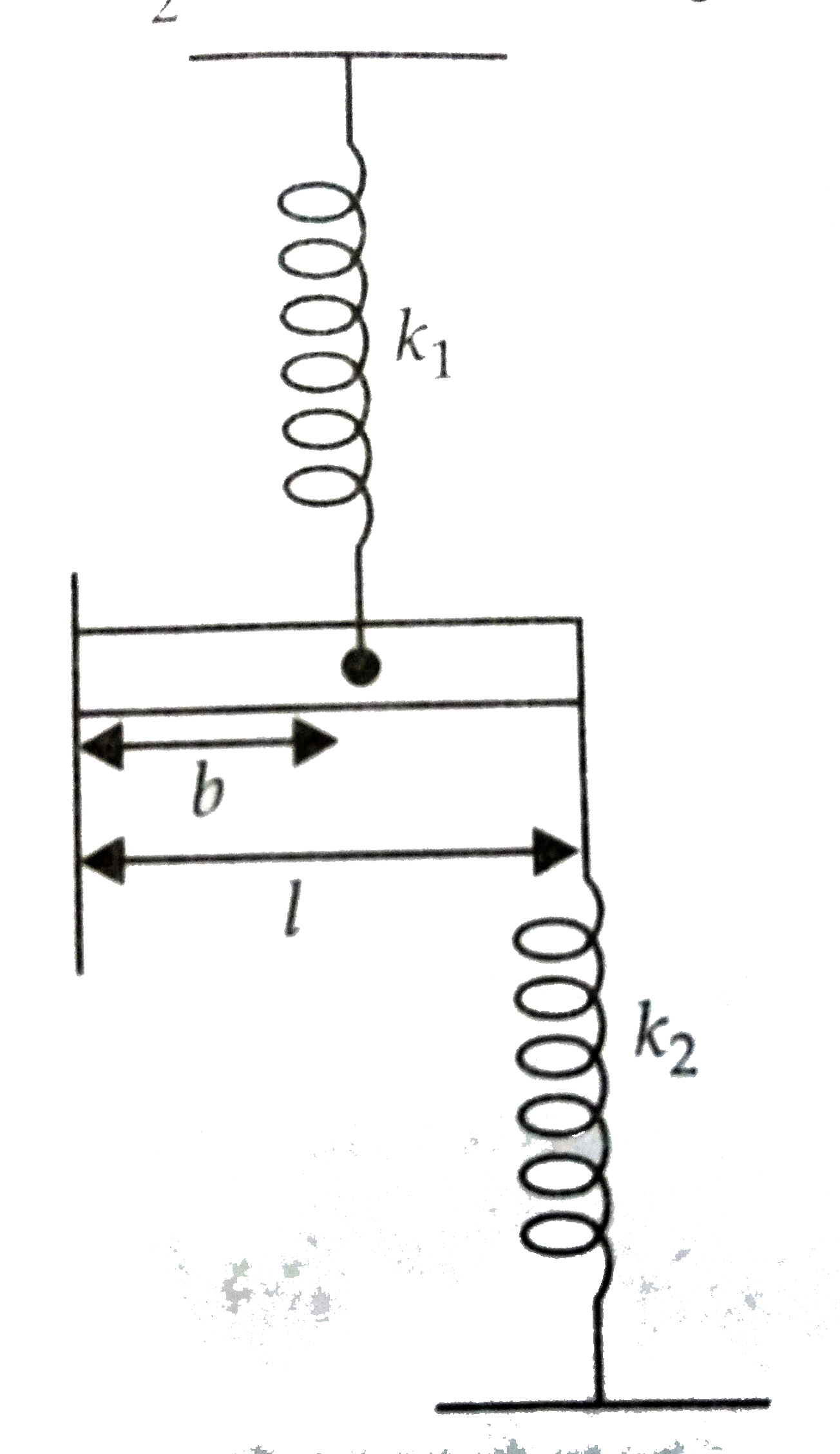
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
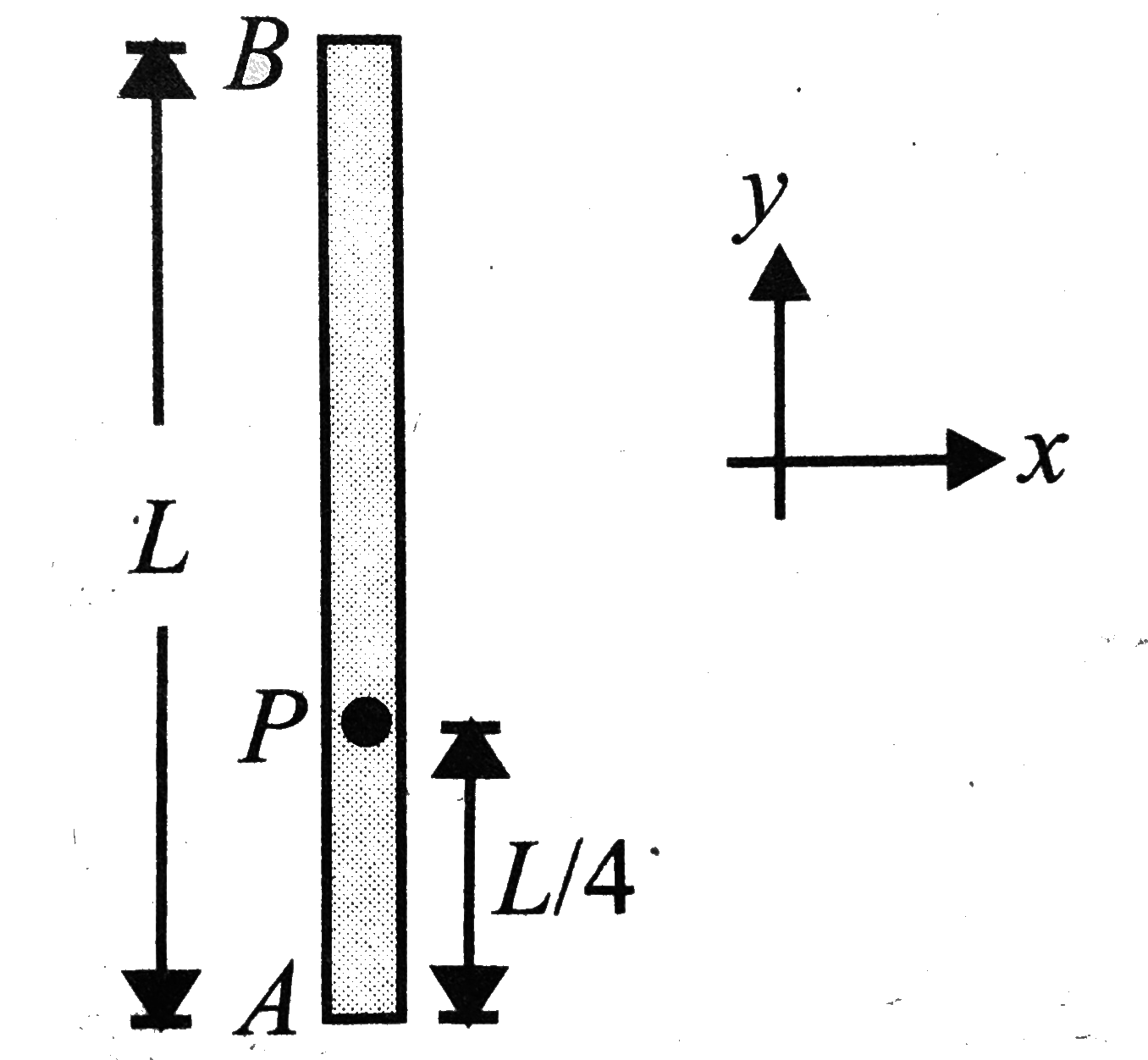
The acceleration of end B of the rod isView SolutionOne end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
[ sin 37∘ = 3/5]
 View Solution
View SolutionOn end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal. as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal. (sin37∘=35).
 View Solution
View SolutionTwo springs A and B(kA=2kB) are stretched by applying forces of equal magnitudes at the force ends. If the energy stored in A is E, that in B is
View Solutiontwo light identical springs of spring constant K are attached horizontally at the two ends of a uniform horizontal rod AB of length l and mass m. the rod is pivoted at its centre 'o' and can rotate freely in horizontal plane . The other ends of the two springs are fixed to rigid supportss as shown in figure . the rod is gently pushed through a small angle and released , the frequency of resulting oscillation is :
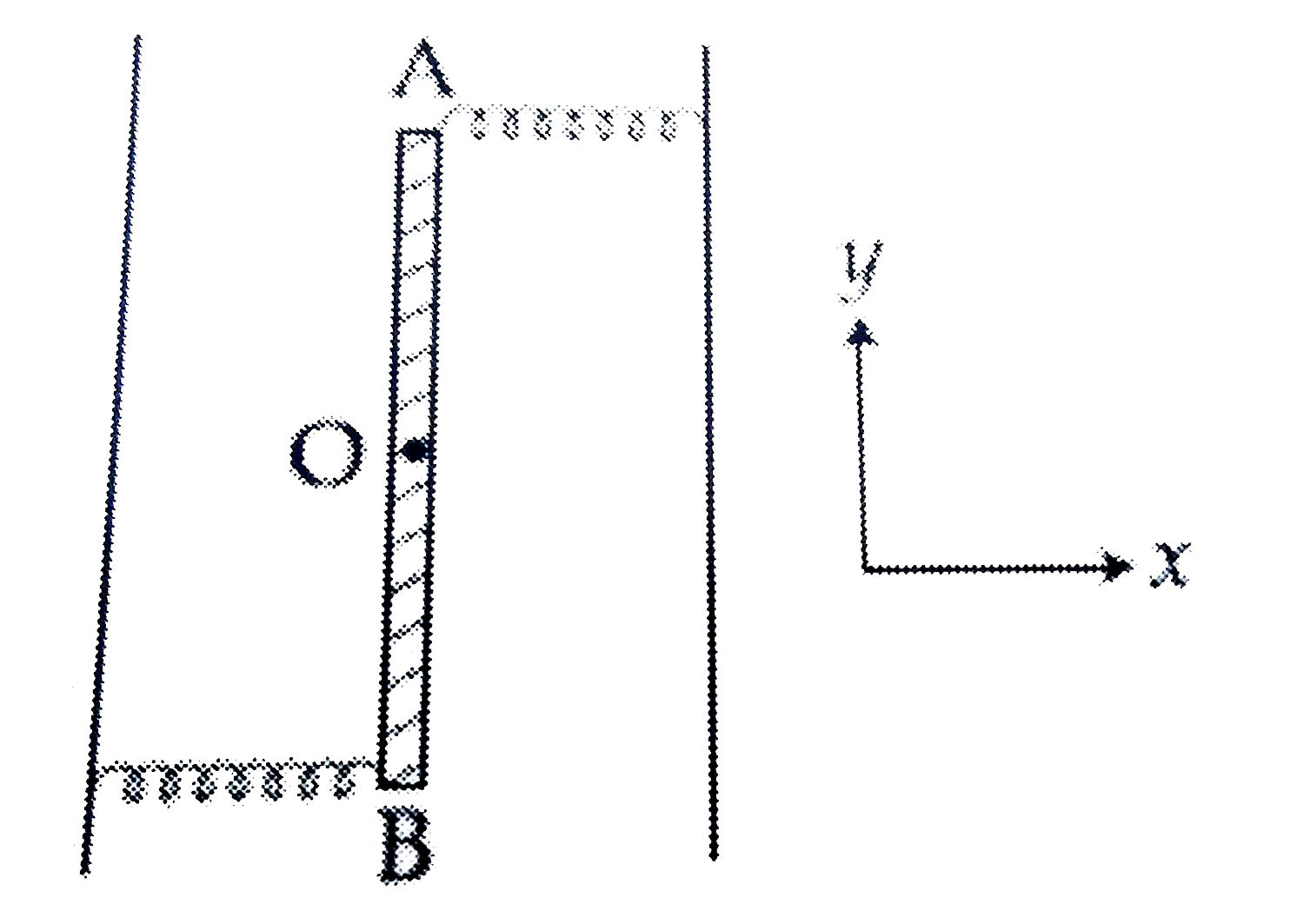 View Solution
View SolutionA vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring , so that the spring is compressed by a distance d. The net work done in the process is
View SolutionTwo bodies A and B of equal mass are suspended from two separate massless springs of spring constant k1andk2 respectively. If the bodies Oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of A to that of B is
View Solution

