A ray of light travelling in air is incident at grazing incidence on a slab with variable refractive index, n (y) =[ky3/2+1]1/2 where k=1m−3/2 and follows path as shown in the figure. What is the total deviation produced by slab when the ray comes out.
![A ray of light travelling in air is incident at grazing incidence on a slab with variable refractive index, n (y) =[k y^(3//2)+1]^(1//2) where k=1 m^(-3//2) and follows path as shown in the figure. What is the total deviation produced by slab when the ray comes out.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_OPT_PHY_XII_C01_E01_028_Q01.png)
60∘
53∘
sin−1(4/9)
no deviation at all
The correct Answer is:D
As n varies 'y', parallel slabs can be taken, and we know in parallel slabs
nrsinir=constant, as n1sini1=1×sin90∘=1=constant
nfinal=nair=1
⇒1=1×sinrFinal
⇒rfinal=90∘
∴ Deviation is zero.
Topper's Solved these Questions
Similar Questions
A ray of light travelling in air is inciden at angle of inciden 30∘ on one surface of slab in which refractive index varies with y. The light travels along the curve y=4x2 ( y and x are in meter) in the slab. Find out the refractive index of the slab at y=1/2m in the slab.
View SolutionA light ray enters from medium A to medium B as shown in the figure. The refractive index of medium B relative to A will be
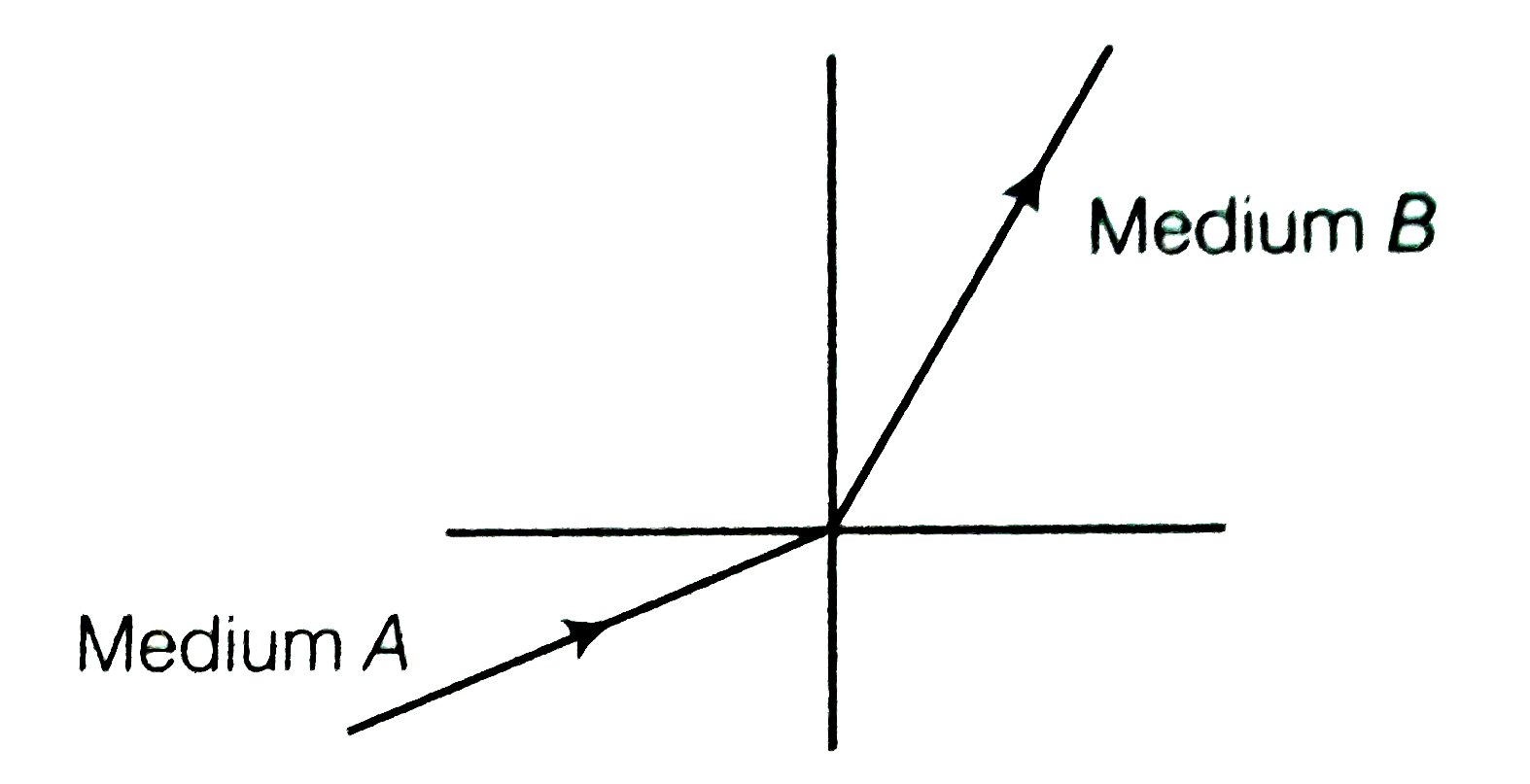View SolutionA ray of light travelling in air is incident at grazing angle (incident angle=90∘) on a long rectangular slab of a transparent medium of thickness t=1.0 (see figure). The point of incidence is the origin A(O,O) .The medium has a variable index of refraction n(y) given by :n(y)=[ky3/2+1]1/2 ,where k=1.0m−3/2.the refractive index of air is 1.0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_RO_C01_E01_029_Q01.pngwh=80%mx-autosty≤=background:white;><br>(i)Obta∈arelationbetweentheslopeofthetrajec→ryoftherayatap∮B(x,y)∈themediumandthe∈cnt∠attˆp∮<br>(ii)obta∈anequationforthetrajec→ryy(x)oftheray∈themedium.<br>(ii)Determinethec∞rd∈ates(x_(1),y_(1))ofthep∮P.where the ray the ray intersects upper surface of the slab -air boundary.
Indicate the path of the ray subsequently.View SolutionA ray of light suffers a minimum deviation when incident on equilateral prism of refractive index √2 The angle of deviation is
View SolutionTwo parts of long cylinder having refractive index √3 and 32 are arranged as shown in figure. When a light ray is incident an one plane surface as shown, total deviation produced in the path of light ray is π3xrad. Then calculate x.
.View SolutionThere is a equilateral prism of refractive index 3 on which a light ray is incident normally on one face as shown in the figure. Find the length of the path traveled by the light ray inside the prism.
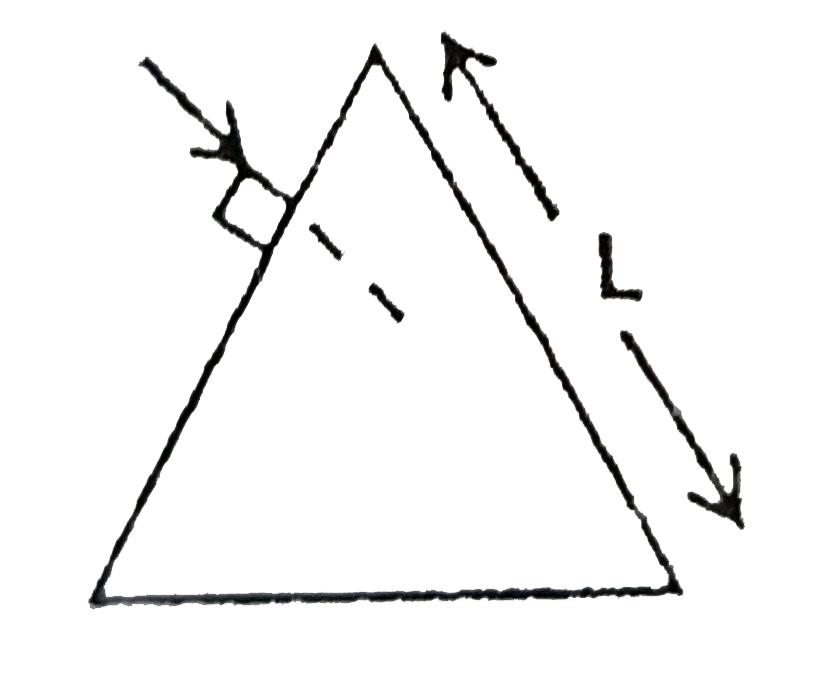View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
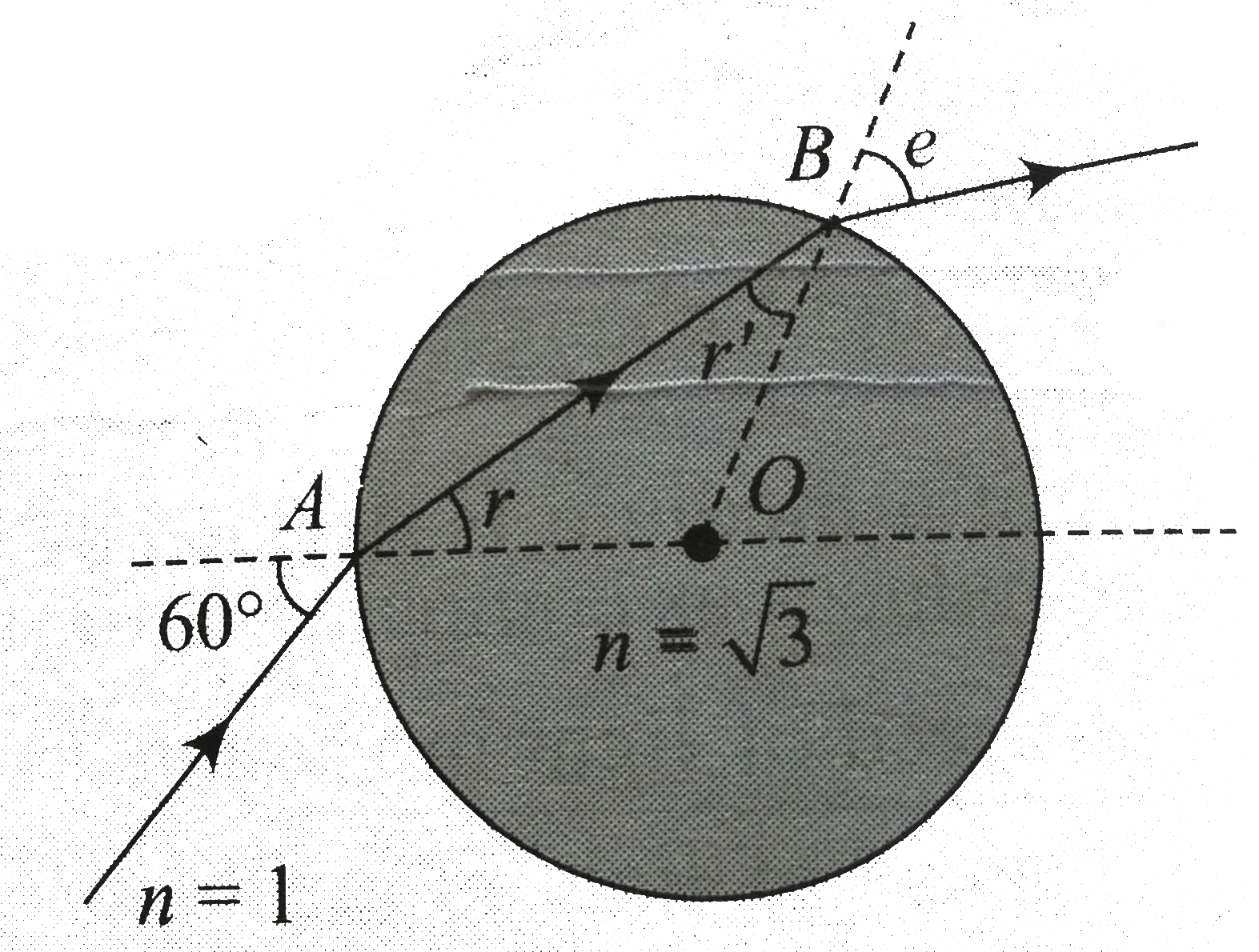View SolutionA ray of light is incident on the surface of a transparent sphere of R.I.μ=√72. After refraction is is internally reflected and refracted out of the sphere as shown in the figure. Find the angle of incidence 'I' so that the total deviation produced is minimum. 'C' is the centre of the sphere.
.View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA ray of light is incident normally on one face of an equilateral prism of refractive index 1.5. The angle of deviation is: (Given sin−1.23=42∘)
View Solution