STATEMENT-1: A lens has two principal focal lengths which may be different in magnitude. STATEMENT-2: The distance of both principal focus from optical centre of lens depend on the two radii of curvature of the lens. Distance of both principal focus from optical centre a lens are same only if radii of curvature of both sides of lens are same
Statement-1 is true, Statement-2: is true, Statement-2 is a correct explanation for Statement-1.
Statement-1 is true, Statement-2: is true, Statement-2 is NOT a correct explanation for Statement-1.
Statement-1 is true but statement-2 is false
Statement-1 is false, Statement-2 is true
The correct Answer is:C
To analyze the two statements provided in the question, we will evaluate each one step by step.
Step 1: Evaluate Statement 1
Statement 1: A lens has two principal focal lengths which may be different in magnitude.
- Explanation: This statement is true. A lens, particularly a double convex or double concave lens, is formed by two surfaces that can have different curvatures. Since the focal length of a lens is dependent on the curvature of its surfaces, it is possible for the two principal focal lengths to differ in magnitude.
Step 2: Evaluate Statement 2
Statement 2: The distance of both principal focus from the optical centre of the lens depends on the two radii of curvature of the lens. The distance of both principal focus from the optical centre of a lens is the same only if the radii of curvature of both sides of the lens are the same.
- Explanation: This statement is partially true but ultimately false due to the use of the word "only." The distance of the principal foci does depend on the radii of curvature, but it also depends on the refractive index of the lens material, as described by the lens maker's formula:
1f=(μ−1)(1r1−1r2)
Here, f is the focal length, μ is the refractive index, and r1 and r2 are the radii of curvature. Therefore, the statement is false because it implies that the radii of curvature alone determine the focal lengths without considering the material's refractive index.
Conclusion
- Final Evaluation:
- Statement 1 is true.
- Statement 2 is false due to the misleading use of the word "only."
Answer
The correct option is that Statement 1 is true, but Statement 2 is false.
---
Statement 1: A lens has two principal focal lengths which may be different in magnitude.
Statement 2: The distance of both principal focus from the optical centre of the lens depends on the two radii of curvature of the lens. The distance of both principal focus from the optical centre of a lens is the same only if the radii of curvature of both sides of the lens are the same.
1f=(μ−1)(1r1−1r2)
Here, f is the focal length, μ is the refractive index, and r1 and r2 are the radii of curvature. Therefore, the statement is false because it implies that the radii of curvature alone determine the focal lengths without considering the material's refractive index.
- Final Evaluation:
- Statement 1 is true.
- Statement 2 is false due to the misleading use of the word "only."
The correct option is that Statement 1 is true, but Statement 2 is false.
Topper's Solved these Questions
Similar Questions
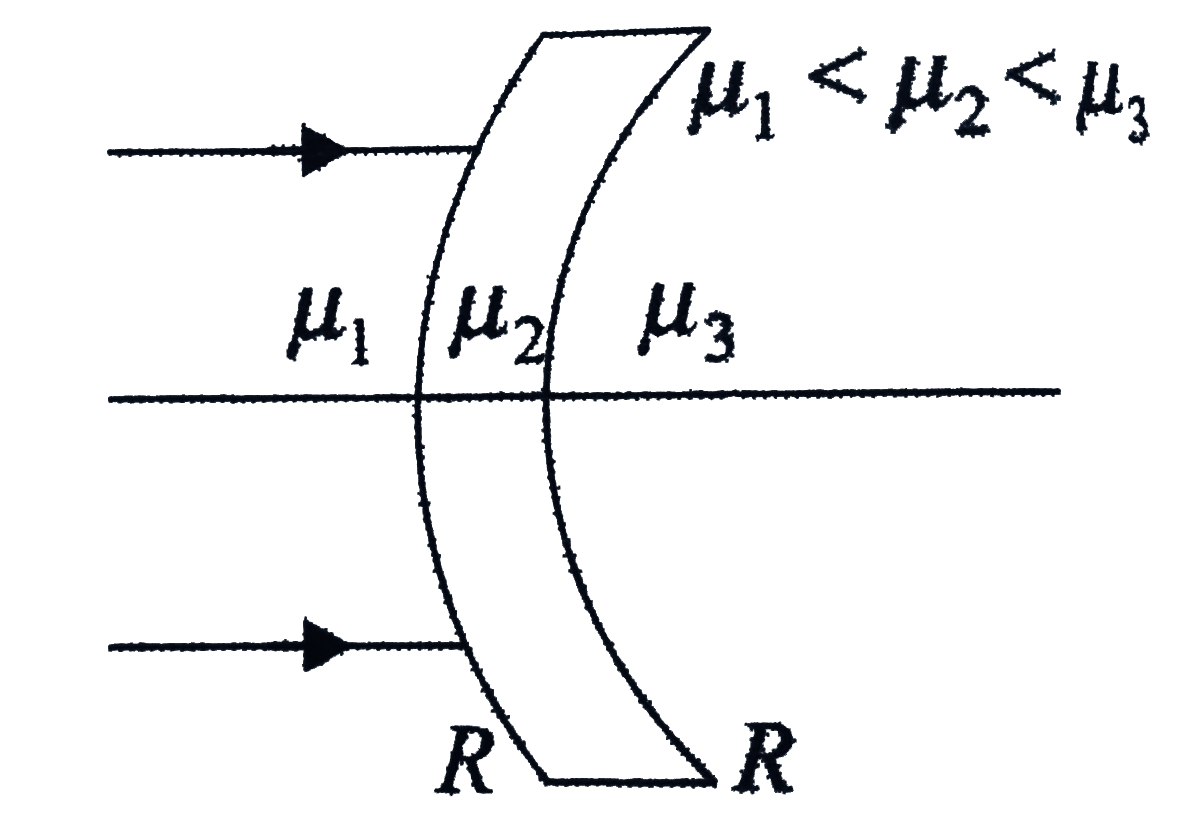
Find the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
View SolutionStatement-1 A lens has two principal focal lengths which may differ
because
Statement -2 : Light can fall on either surface of the lens. The two principal focal lengths differ when medium on the two sides has different refractive indices.
View Solution
Knowledge Check
Assertion : The focal length of an equiconvex lens placed in air is equal to radius of curvature of either face.
Reason : For an equiconvex lens radius of curvature of both the faces is same.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true and reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.Radii of curvature of a converging lens are in the ratio 1:2. Its focal length is 6cm and refractive index is 1.5. Then its radii of curvature are
A9cm and 18cmB6cm and 12cmC3cm and 6cmD4.5cm and 9cm
A biconvex lens (μ=1.5) has radius of curvature 20cm (both).
find its focal length.
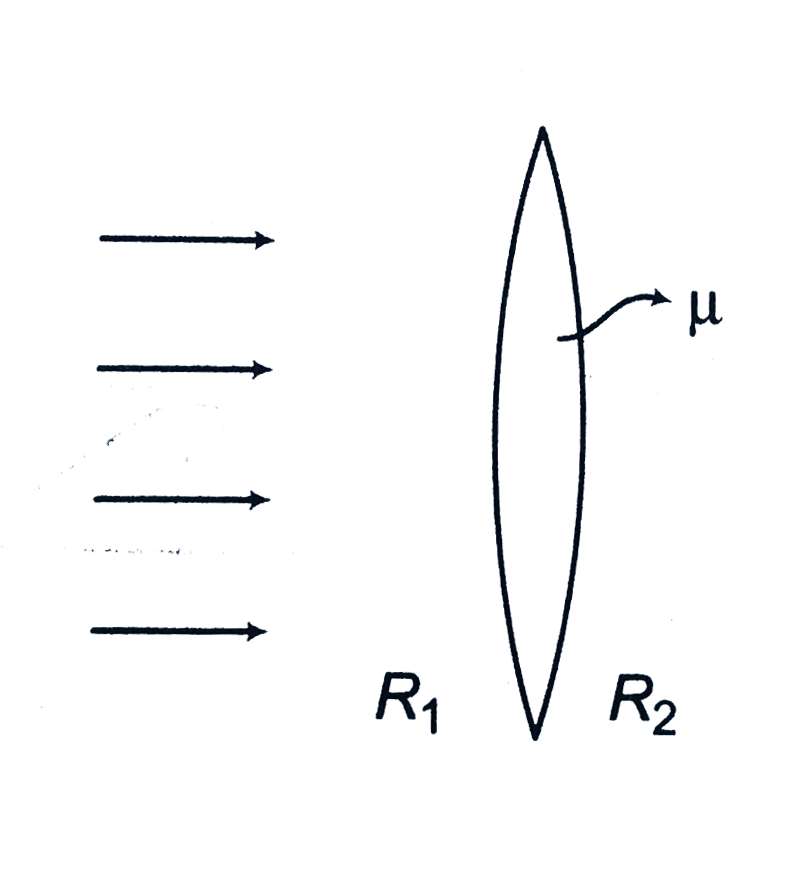
View SolutionRadii of curvature of a converging lens are in the ratio 1:2. Its focal length is 6cm and refractive index is 1:5. Then, its radii of curvature are…
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
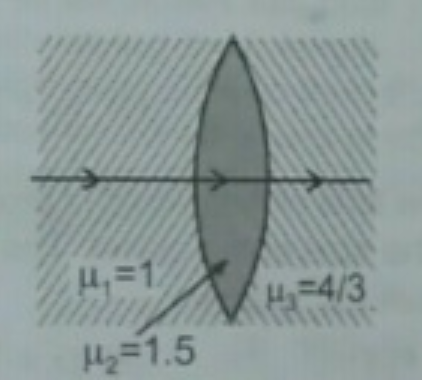
View SolutionIf radii of curvature of both convex surfaces is 20 cm, then focal length of the lens for an object placed in air in the given arrangement is
View SolutionA point object is places on the principal axis of a thin lens with parallel curved boundaries, i.e., having same radii of curvature. Discuss about the position of the image formed.
View Solution
