For the same potential difference, a potentiometer wire is replaced by another one of a high specific resistance. The potential gradient then (r=Rh=0)
decreases
remains same
increases
data is incomplete
The correct Answer is:B
To solve the problem, we need to analyze the effect of replacing a potentiometer wire with another wire of higher specific resistance on the potential gradient.
1. Understanding Potential Gradient:
The potential gradient (E) is defined as the potential difference (V) across a length (L) of the wire. Mathematically, it can be expressed as:
E=VL
where E is the potential gradient, V is the potential difference, and L is the length of the wire.
2. Given Conditions:
- The potential difference (V) remains the same for both wires.
- The length (L) of the potentiometer wire is assumed to be the same for both cases.
- The specific resistance (ρ) of the new wire is higher than that of the original wire.
3. Effect of Specific Resistance:
The specific resistance (ρ) of the wire does not appear in the formula for potential gradient. The potential gradient depends only on the potential difference and the length of the wire. Therefore, even if the specific resistance increases, the potential gradient remains unchanged as long as the potential difference and length are constant.
4. Conclusion:
Since both the potential difference (V) and the length (L) remain the same, the potential gradient (E) will also remain the same. Thus, we conclude:
E=VL(remains constant)
Final Answer:
The potential gradient remains the same when the potentiometer wire is replaced by another one of higher specific resistance, given that the potential difference and length are unchanged.
---
The potential gradient (E) is defined as the potential difference (V) across a length (L) of the wire. Mathematically, it can be expressed as:
E=VL
where E is the potential gradient, V is the potential difference, and L is the length of the wire.
- The potential difference (V) remains the same for both wires.
- The length (L) of the potentiometer wire is assumed to be the same for both cases.
- The specific resistance (ρ) of the new wire is higher than that of the original wire.
The specific resistance (ρ) of the wire does not appear in the formula for potential gradient. The potential gradient depends only on the potential difference and the length of the wire. Therefore, even if the specific resistance increases, the potential gradient remains unchanged as long as the potential difference and length are constant.
Since both the potential difference (V) and the length (L) remain the same, the potential gradient (E) will also remain the same. Thus, we conclude:
E=VL(remains constant)
The potential gradient remains the same when the potentiometer wire is replaced by another one of higher specific resistance, given that the potential difference and length are unchanged.
Topper's Solved these Questions
Similar Questions
How are the potential difference (V), current (I) and resistance (R) related ?
View SolutionIf the resistance of potentiometer wire is 15r then calculate the balance length l
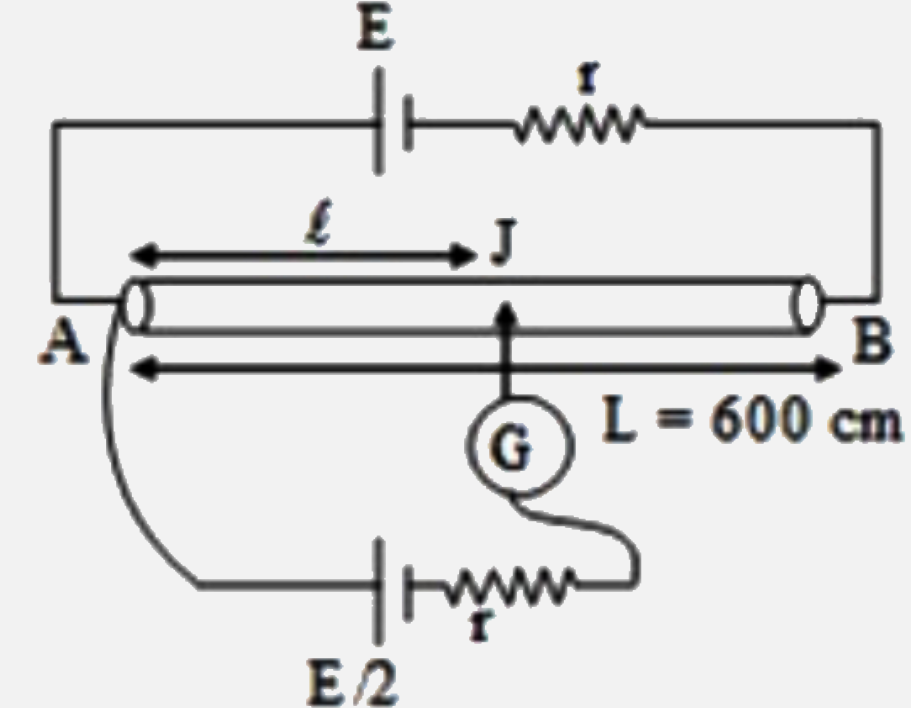 View Solution
View SolutionA capacitor is conneted to a cell emf E having some internal resistance r. The potential difference across the
View SolutionIf the resistivity of a potentiometer wire be ρ and area of cross-section be A , then what will be potential gradient along the wire
View SolutionThe length of a potentiometer wire is 10m and a potential difference of 2 volt is applied to its ends. If the length of its wire is increased by 1m, the value of potential gradient in volt/m will be (potential difference across potentiometer wire remain same)
View SolutionAn ammeter A of finite resistance, and a resistor R are joined in series to an ideal cell C. A potentiometer P is joined in parallel to R. The ammeter reading is I0 and the potentiometer reading is V0. P is now replaced by a voltmeter of finite resistance. The ammeter reading now is I and the voltmeter reading is V.
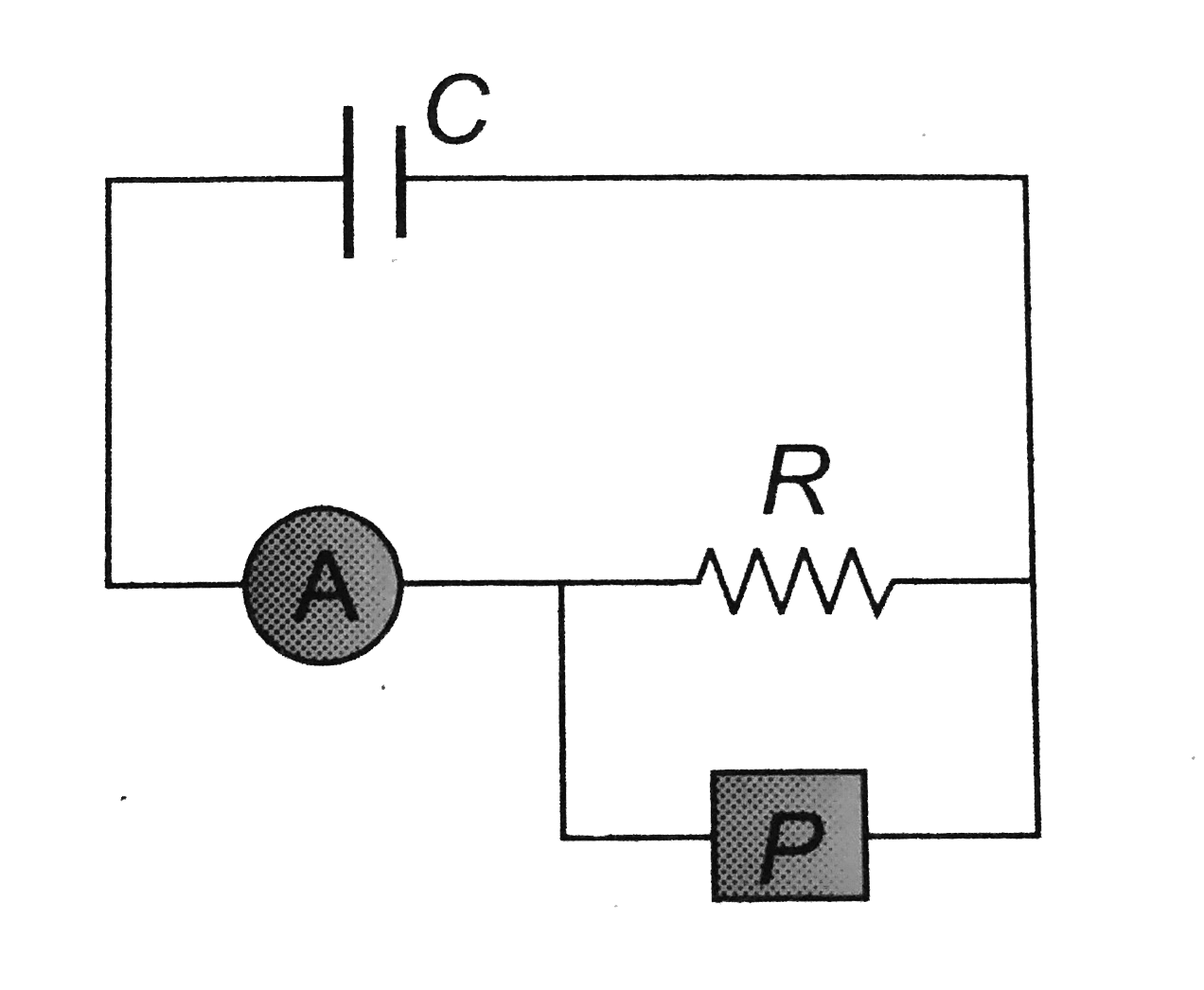 View Solution
View SolutionA 2 V battery, a 990Ω resistor and a potentiometer of 2 m length, all are connected in series of the resistance of potentiometer wire is 10Ω, then the potential gradient of the potentiometer wire is
View SolutionA 2 V battery, a 990Ω resistor and a potentiometer of 2 m length, all are connected in series of the resistance of potentiometer wire is 10Ω, then the potential gradient of the potentiometer wire is
View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
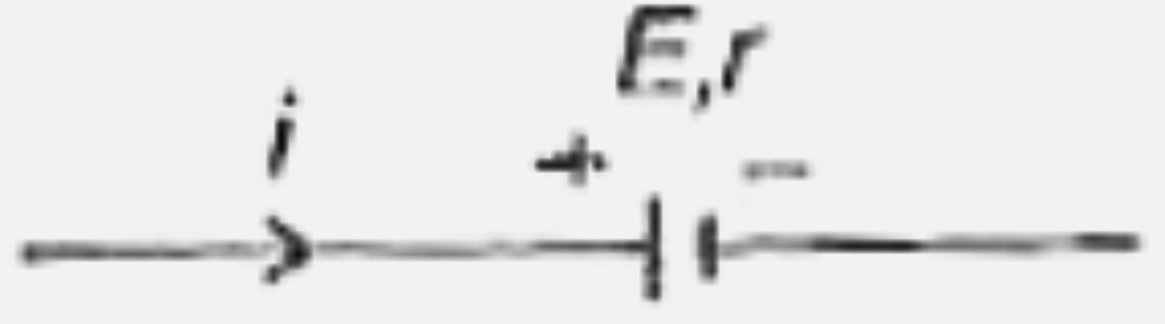 View Solution
View SolutionThe potentiometer wire 10m long and 20 ogm resistance is connected to a 3 volt emf battery and a 10ohm resistance. The value of potential gradient in volt/m of the wire will be
View Solution

