There is a voltmeter in a circuit. In order to triple its range, the resistance of how much value should be used?
2R
R/2
3R
4R
The correct Answer is:A
To solve the problem of determining the resistance needed to triple the range of a voltmeter, we can follow these steps:
Step 1: Understand the Basics
A voltmeter is used to measure the potential difference (voltage) across a component in a circuit. It is connected in parallel with the component whose voltage is being measured.
Step 2: Define Initial Conditions
Let:
- V1 = initial voltage measured by the voltmeter
- R = internal resistance of the voltmeter
- I = current flowing through the circuit
According to Ohm's Law, the voltage across the resistor can be expressed as:
V1=I⋅R
Step 3: Define New Conditions
To triple the range of the voltmeter, we need to find the new voltage V2:
V2=3V1
Step 4: Set Up the New Equation
When we add a new resistance R′ in parallel with the voltmeter, the new voltage can be expressed as:
V2=I⋅R′
Step 5: Substitute for V2
We can substitute V2 from the previous step:
3V1=I⋅R′
Step 6: Substitute for V1
Now, substitute V1 from the first equation:
3(I⋅R)=I⋅R′
Step 7: Cancel Out Current
Since current I is the same in both cases, we can cancel it out (assuming I≠0):
3R=R′
Step 8: Conclusion
Thus, the resistance R′ that should be used to triple the range of the voltmeter is:
R′=3R
Final Answer
The resistance value needed to triple the range of the voltmeter is 3R.
---
A voltmeter is used to measure the potential difference (voltage) across a component in a circuit. It is connected in parallel with the component whose voltage is being measured.
Let:
- V1 = initial voltage measured by the voltmeter
- R = internal resistance of the voltmeter
- I = current flowing through the circuit
V1=I⋅R
To triple the range of the voltmeter, we need to find the new voltage V2:
V2=3V1
When we add a new resistance R′ in parallel with the voltmeter, the new voltage can be expressed as:
V2=I⋅R′
We can substitute V2 from the previous step:
3V1=I⋅R′
Now, substitute V1 from the first equation:
3(I⋅R)=I⋅R′
Since current I is the same in both cases, we can cancel it out (assuming I≠0):
3R=R′
Thus, the resistance R′ that should be used to triple the range of the voltmeter is:
R′=3R
The resistance value needed to triple the range of the voltmeter is 3R.
Topper's Solved these Questions
Similar Questions
A voltmeter with a resistance 50×103Ω is used to measure voltage in a circuit. To increase its range to 3 times, the additional resistance to be put in series is
View SolutionIf the reading of the ideal voltmeter shown in the circuit is 2V the internal resistance of the two identical cells is
_2019_CBT5_E01_030_Q01.png) View Solution
View Solution
Knowledge Check
- Question 1 - Select One
When a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
A1100B1000C900D800
The ammeter (A) and voltmeter (V) in the given circuit are ideal but the galvanometer has a resistance of 2Ω In steady state
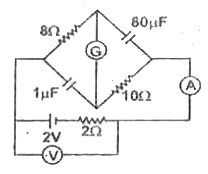 View Solution
View SolutionWhat is the resistance of voltmeter shown in the circuit ?
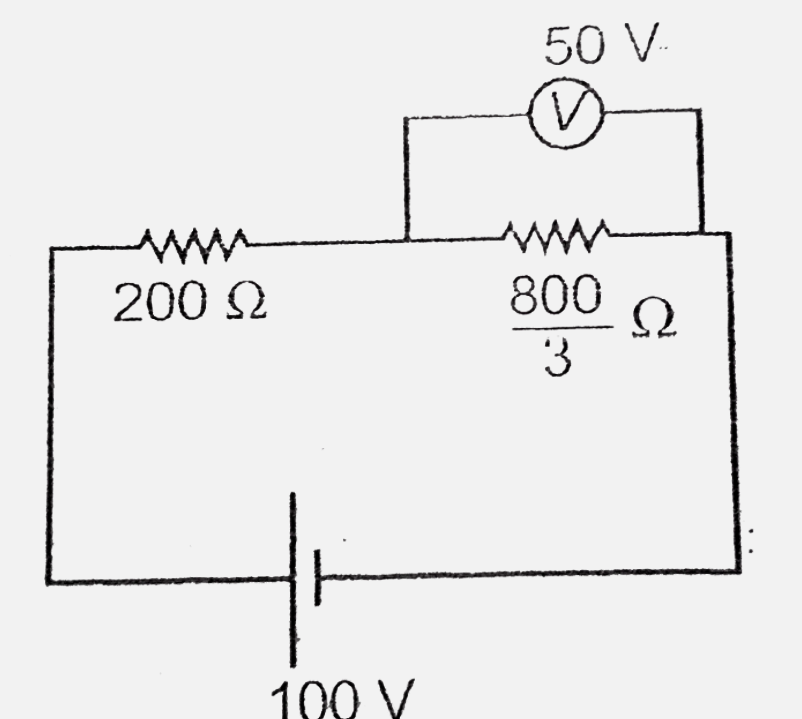 View Solution
View SolutionIn the circuit figure, the voltmeter reads 30 V. The resistance of the voltmeter is
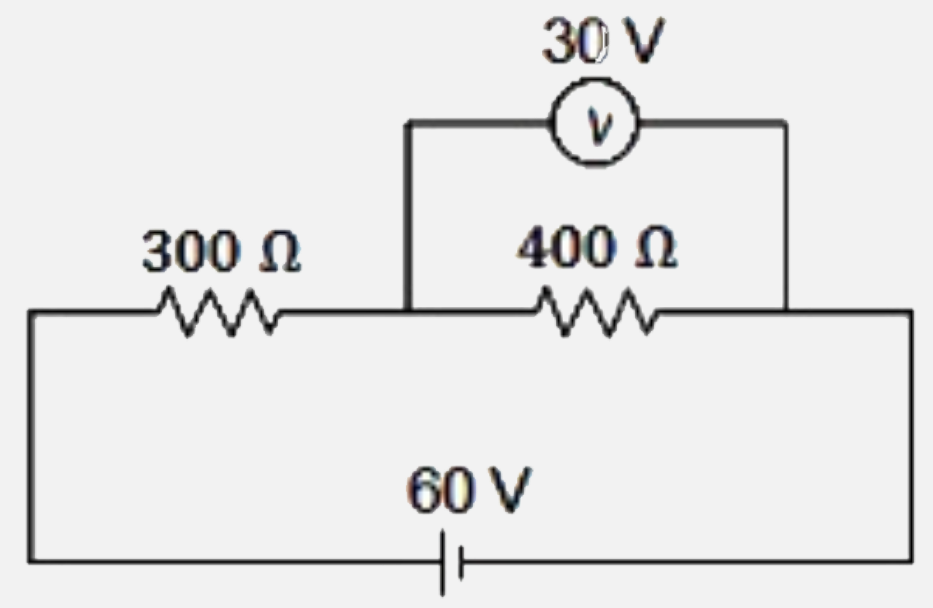 View Solution
View SolutionIn the adjoining circuit, the e.m.f. of the cell is 2 volt and the internal resistance is negligible. The resistance of the voltmeter is 80ohm. The reading of the voltmeter will be
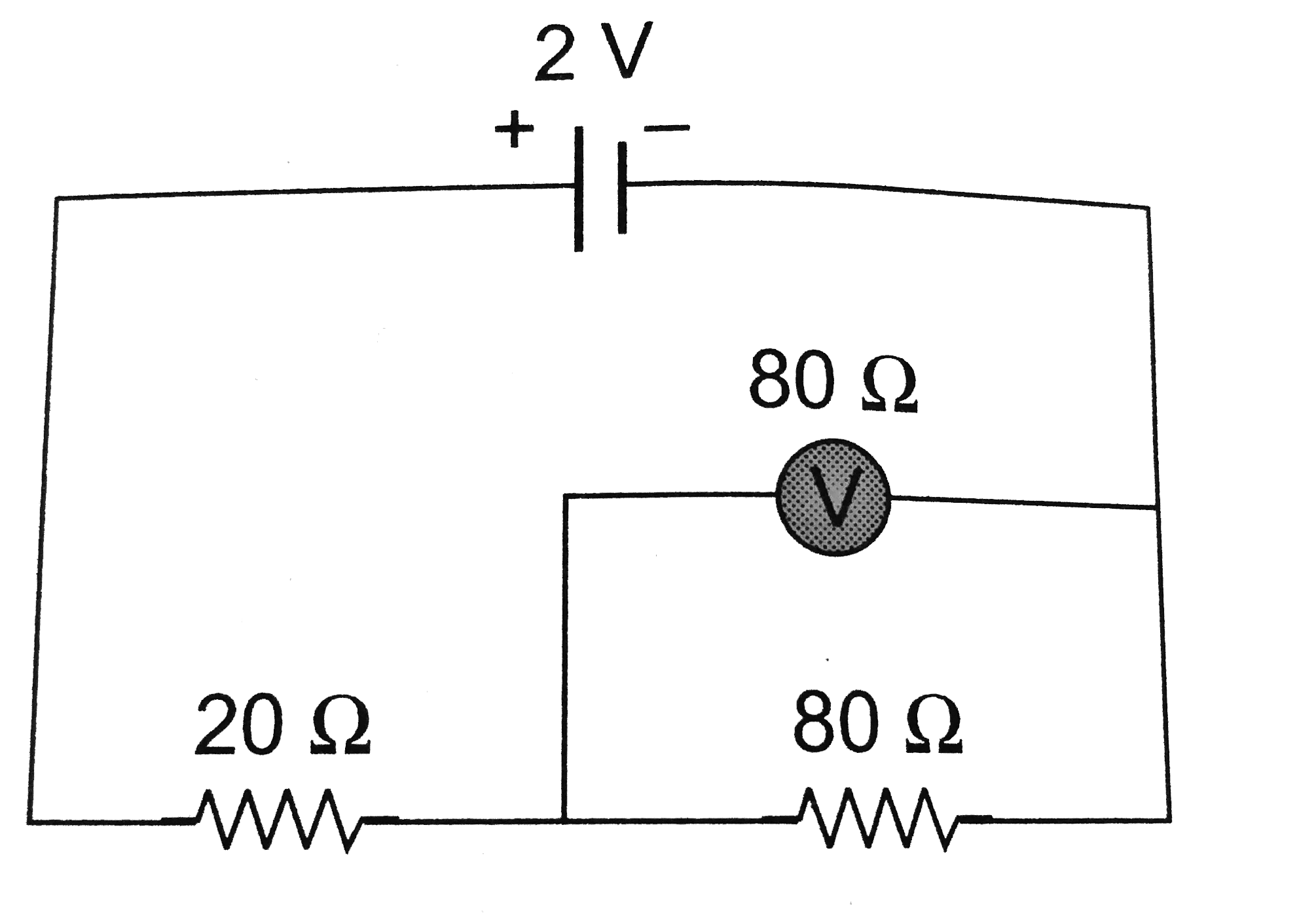 View Solution
View SolutionAssertion : Voltmeter is connected in parallel with the circuit
Reason : Resistance of a voltmeter is very large.View SolutionIn the given circuit, the voltmeter records 5 volt. The resistance of the voltmeter in Ω is
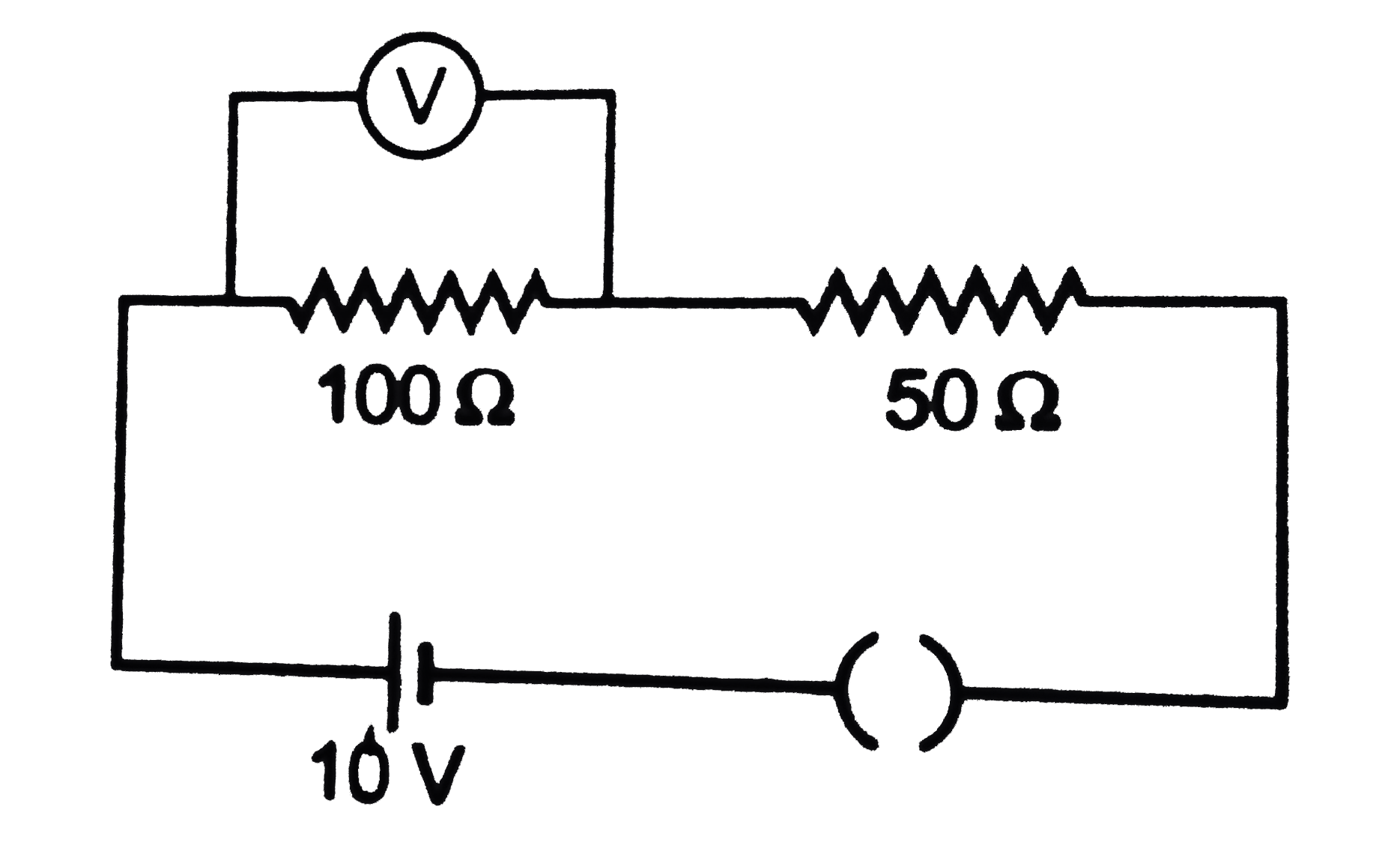 View Solution
View SolutionIn the given circuit, the voltmeter records 5 V. The resistance of the voltmeter in Ω is
 View Solution
View Solution

