A capacitor when charged by a potential difference of 200 Volts, stores a charge of 0.1C. By discharging energy liberated by the capacitor is-
10 J
20 J
The correct Answer is:C
To solve the problem of finding the energy liberated by a capacitor when it is discharged, we can follow these steps:
1. Identify the given values:
- Potential difference (V) = 200 Volts
- Charge (Q) = 0.1 Coulombs
2. Use the formula for energy stored in a capacitor:
The energy (U) stored in a capacitor can be calculated using the formula:
U=12CV2
However, we do not have the capacitance (C) directly.
3. Relate capacitance to charge and voltage:
We know that the capacitance (C) can be expressed as:
C=QV
where Q is the charge and V is the voltage.
4. Substitute C in the energy formula:
Substitute C=QV into the energy formula:
U=12(QV)V2
5. Simplify the expression:
Simplifying the expression gives:
U=12QV
Here, one V from V2 cancels out with the V in the denominator.
6. Substitute the known values:
Now, substitute the values of Q and V into the equation:
U=12×0.1C×200V
7. Calculate the energy:
- First, calculate 12×200=100.
- Then, multiply by 0.1:
U=100×0.1=10Joules
8. Conclusion:
The energy liberated by the capacitor when discharged is 10 Joules.
- Potential difference (V) = 200 Volts
- Charge (Q) = 0.1 Coulombs
The energy (U) stored in a capacitor can be calculated using the formula:
U=12CV2
However, we do not have the capacitance (C) directly.
We know that the capacitance (C) can be expressed as:
C=QV
where Q is the charge and V is the voltage.
Substitute C=QV into the energy formula:
U=12(QV)V2
Simplifying the expression gives:
U=12QV
Here, one V from V2 cancels out with the V in the denominator.
Now, substitute the values of Q and V into the equation:
U=12×0.1C×200V
- First, calculate 12×200=100.
- Then, multiply by 0.1:
U=100×0.1=10Joules
The energy liberated by the capacitor when discharged is 10 Joules.
Topper's Solved these Questions
Similar Questions
A parallel plate capacitor is charged to a potential difference of 10 volts. After disconnecting the battery, distance between the plates of capacitor is decreased by using nonconducting handles. The potential difference between the plates will
View SolutionA parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
View Solution
Knowledge Check
A capacitor is charged through a potential difference of 200 V, when 0.1C charge is stored in it. The amount of energy released by it, when it is discharged is
A5 JB10 JC20 JD2.5 JA parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
AincreasesBdecreaseCdoes not chargeDbecomes zero
A parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
View SolutionAn ideal capacitor of capacitance 0.2μF is charged to a potential difference of 10V. The charging battery is than disconnected. The capacitor is then connected to an ideal inductor of self inductance 0.5mH. The current at a time when the potential difference across the capacitor is 5V is :
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View SolutionFind the charge stored in the capacitor.
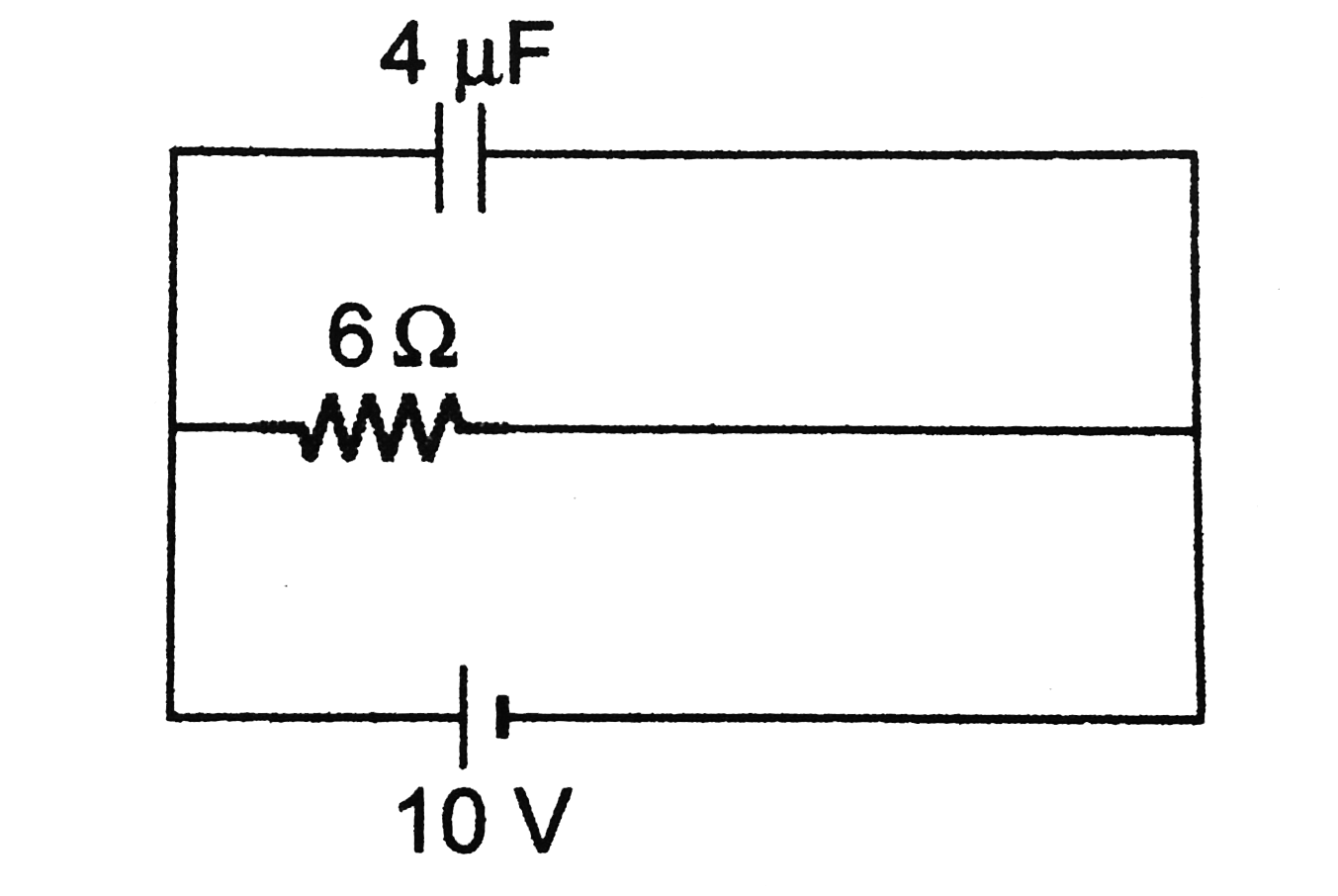
View SolutionFind the charge stored in the capacitor.
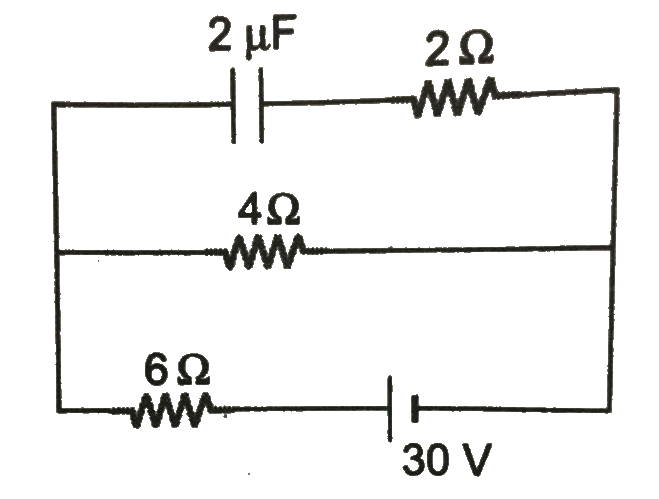
View SolutionFind the charge stored in the capacitor.
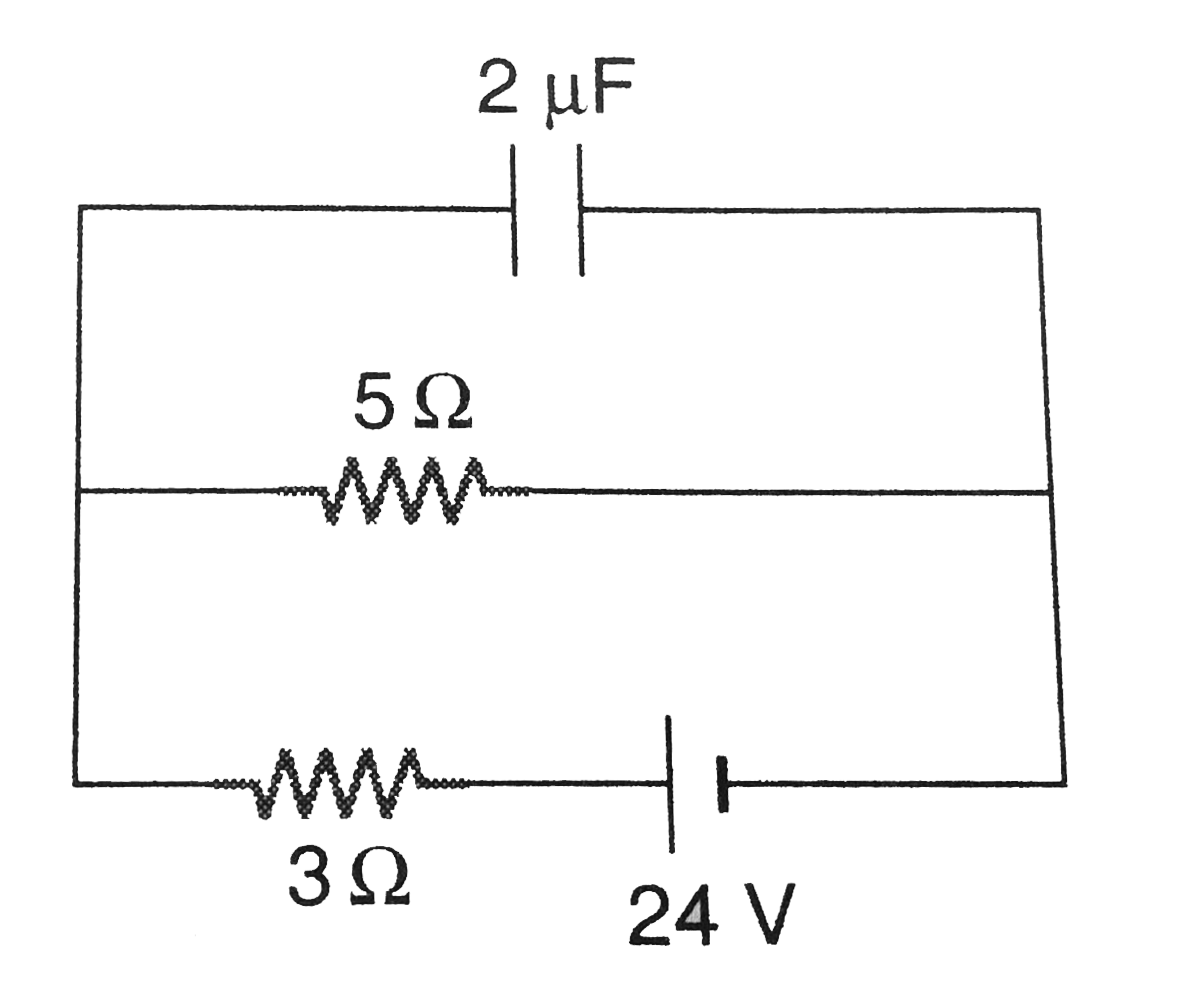
View Solution