Sometimes positive charged particle comes from space towards earth with high velocity. Its deviation due to the magnetic field of earth will be:
towards north
towards south
towards west
towards east
The correct Answer is:D
To solve the question regarding the deviation of a positively charged particle (like a proton) moving towards Earth due to the Earth's magnetic field, we can follow these steps:
1. Understand the Earth's Magnetic Field:
- The Earth can be visualized as a giant magnet with a magnetic North Pole and a South Pole. The magnetic field lines emerge from the magnetic South Pole and enter at the magnetic North Pole.
2. Identify the Direction of the Magnetic Field:
- In the context of the question, we can assume that the magnetic field (B) is directed from the South Pole to the North Pole, which means it points downwards towards the surface of the Earth in the Northern Hemisphere.
3. Determine the Charge and Velocity of the Particle:
- The particle in question is positively charged (like a proton) and is moving towards the Earth with a high velocity (V).
4. Use the Right-Hand Rule:
- To find the direction of the force acting on the charged particle due to the magnetic field, we can apply the right-hand rule.
- According to the right-hand rule, point your thumb in the direction of the velocity (V) of the charged particle and your fingers in the direction of the magnetic field (B). The direction your palm pushes will give you the direction of the magnetic force (F) acting on the particle.
5. Apply the Right-Hand Rule:
- If we assume the particle is moving horizontally towards the Earth (let's say from the top of the page downwards), and the magnetic field is directed downwards (into the page), we can apply the right-hand rule:
- Thumb points in the direction of V (downwards).
- Fingers point in the direction of B (downwards).
- The palm will face towards the east.
6. Conclusion:
- The positively charged particle will be deflected towards the east due to the magnetic force acting on it as it travels through the Earth's magnetic field.
Final Answer:
The deviation of the positively charged particle due to the magnetic field of the Earth will be towards the east.
- The Earth can be visualized as a giant magnet with a magnetic North Pole and a South Pole. The magnetic field lines emerge from the magnetic South Pole and enter at the magnetic North Pole.
- In the context of the question, we can assume that the magnetic field (B) is directed from the South Pole to the North Pole, which means it points downwards towards the surface of the Earth in the Northern Hemisphere.
- The particle in question is positively charged (like a proton) and is moving towards the Earth with a high velocity (V).
- To find the direction of the force acting on the charged particle due to the magnetic field, we can apply the right-hand rule.
- According to the right-hand rule, point your thumb in the direction of the velocity (V) of the charged particle and your fingers in the direction of the magnetic field (B). The direction your palm pushes will give you the direction of the magnetic force (F) acting on the particle.
- If we assume the particle is moving horizontally towards the Earth (let's say from the top of the page downwards), and the magnetic field is directed downwards (into the page), we can apply the right-hand rule:
- Thumb points in the direction of V (downwards).
- Fingers point in the direction of B (downwards).
- The palm will face towards the east.
- The positively charged particle will be deflected towards the east due to the magnetic force acting on it as it travels through the Earth's magnetic field.
The deviation of the positively charged particle due to the magnetic field of the Earth will be towards the east.
Topper's Solved these Questions
Similar Questions
Knowledge Check
When a positively charged particle enters a uniform magnetic field with uniform velocity, its trajectory can be
a) a straight line b) a circle c) a helixA(i) onlyB(i) or (ii)C(i) or (iii)Dany one of (i),(ii) and (iii)
Positively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
View SolutionA velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
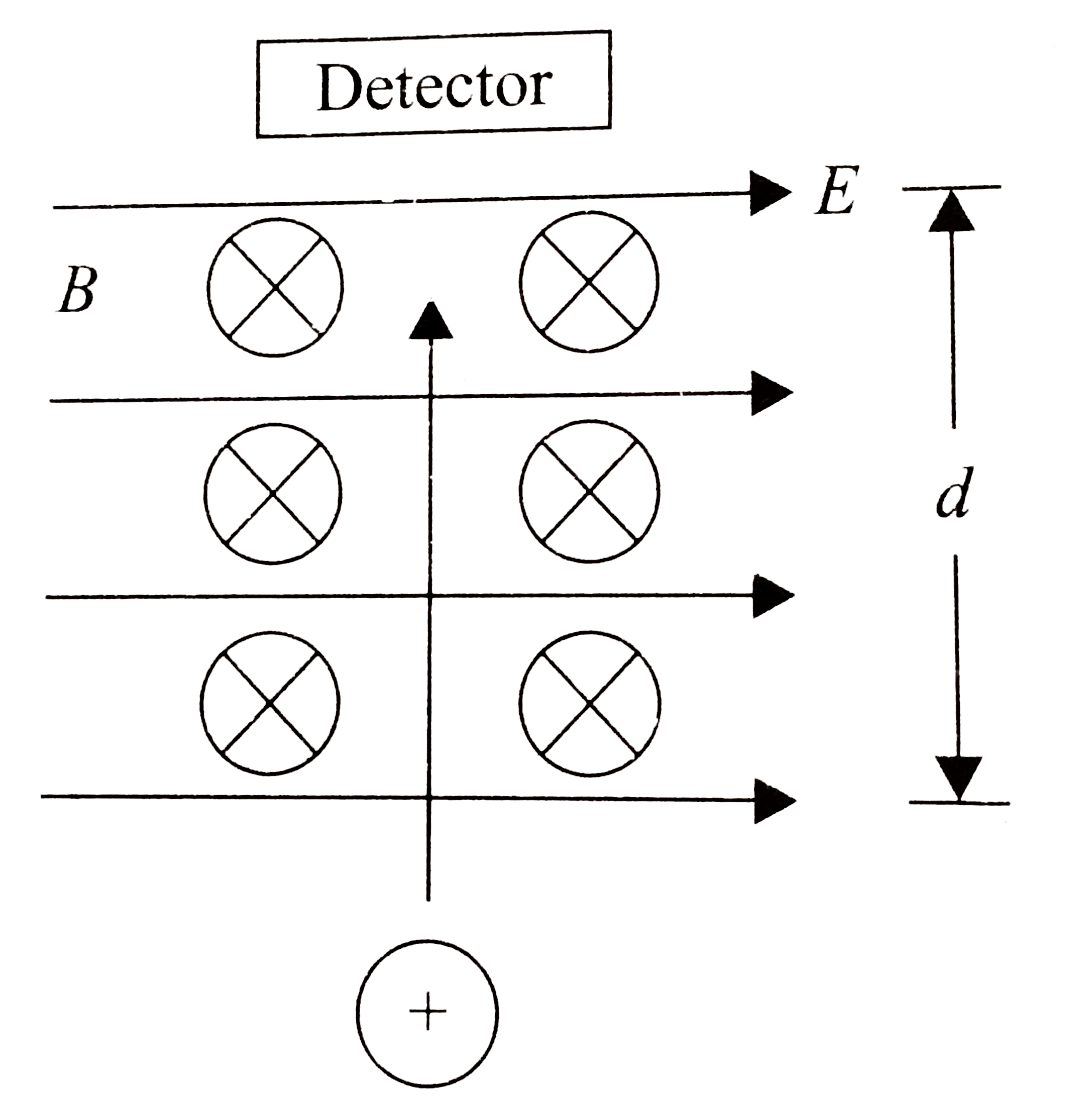
The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?
View SolutionThe path of a charged particle in a uniform magnetic field, when the velocity and the magnetic field are perpendicular to each other is a
View SolutionA charged particle enters a unifrom magnetic field with velocity vector at an angle of 45∘ with the magnetic field . The pitch of the helical path followed by the particles is ρ . The radius of the helix will be
View SolutionA positively-charged particle (alpha particle) projected towards west is deflected towards north by a magnetic field. The direction of magnetic field is:
(a) towards south
(b) towards east
(c) downward
(d) upward
View SolutionMagnetic field exist in the space and given as →B=−B0l2x2ˆk, where B0and l positive constants. A particle having positive charge 'q' and mass 'm' is pojected wit speed 'v0' along positive x axis from the origin. What is the maimum distance of the charged particle from the y-axis before it turns back due to the magnetic field. (Ignore any interaction other than magnetic field)
View SolutionIn a region of space, both electric and magnetic field are present simultaneously in opposite direction. A positively charged particle is projected with certain speed an angle θ(<90∘) with magnetic field. It will move in a
View Solution