A velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
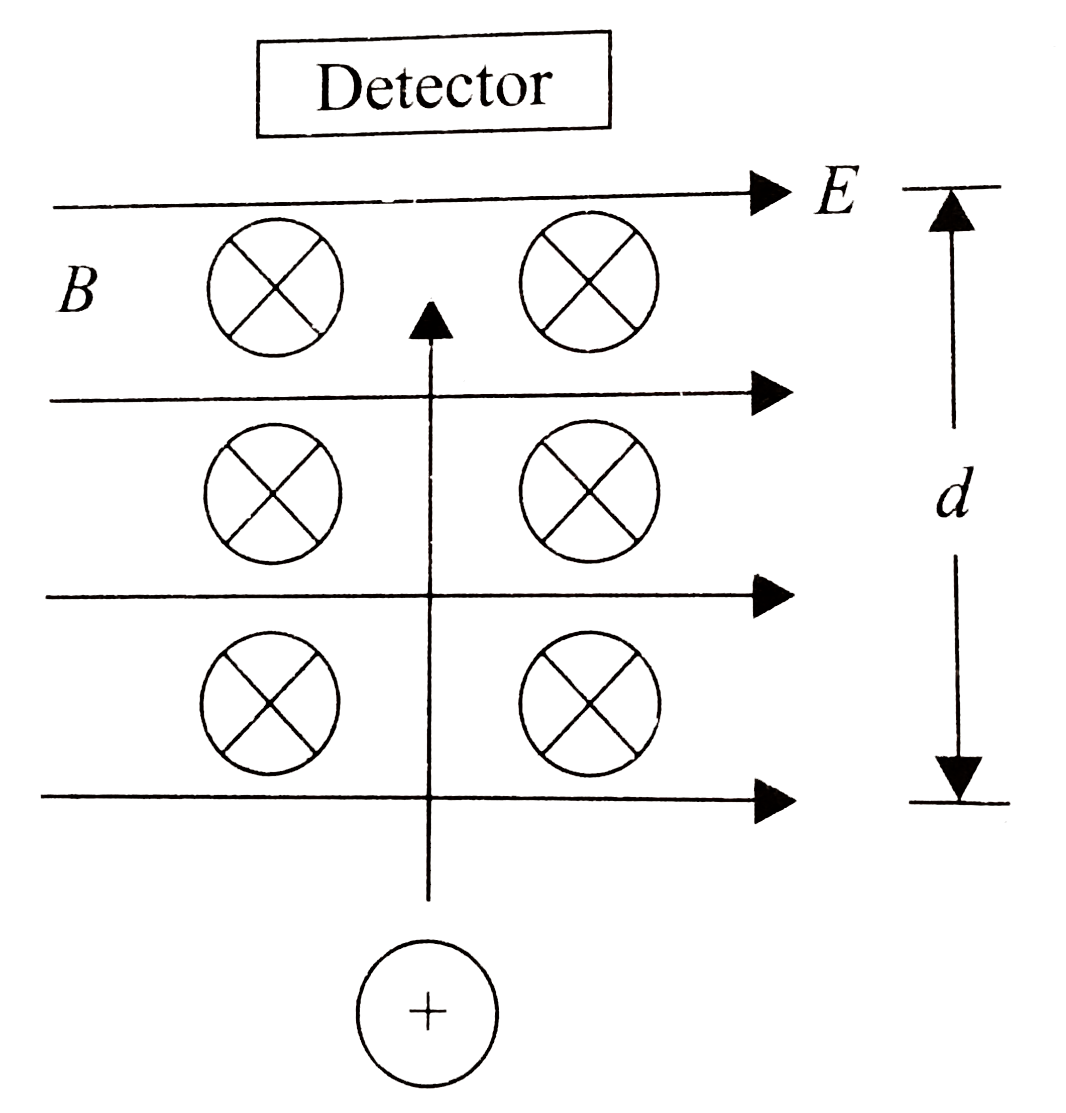
The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?
Bq2E
(Eq2B)
(BE)
(EB)
The correct Answer is:D
At speed v0=Fe=Fm
qE=qv0B⇒v0=EB
Hence (d) is correct option.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
Similar Questions
A velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
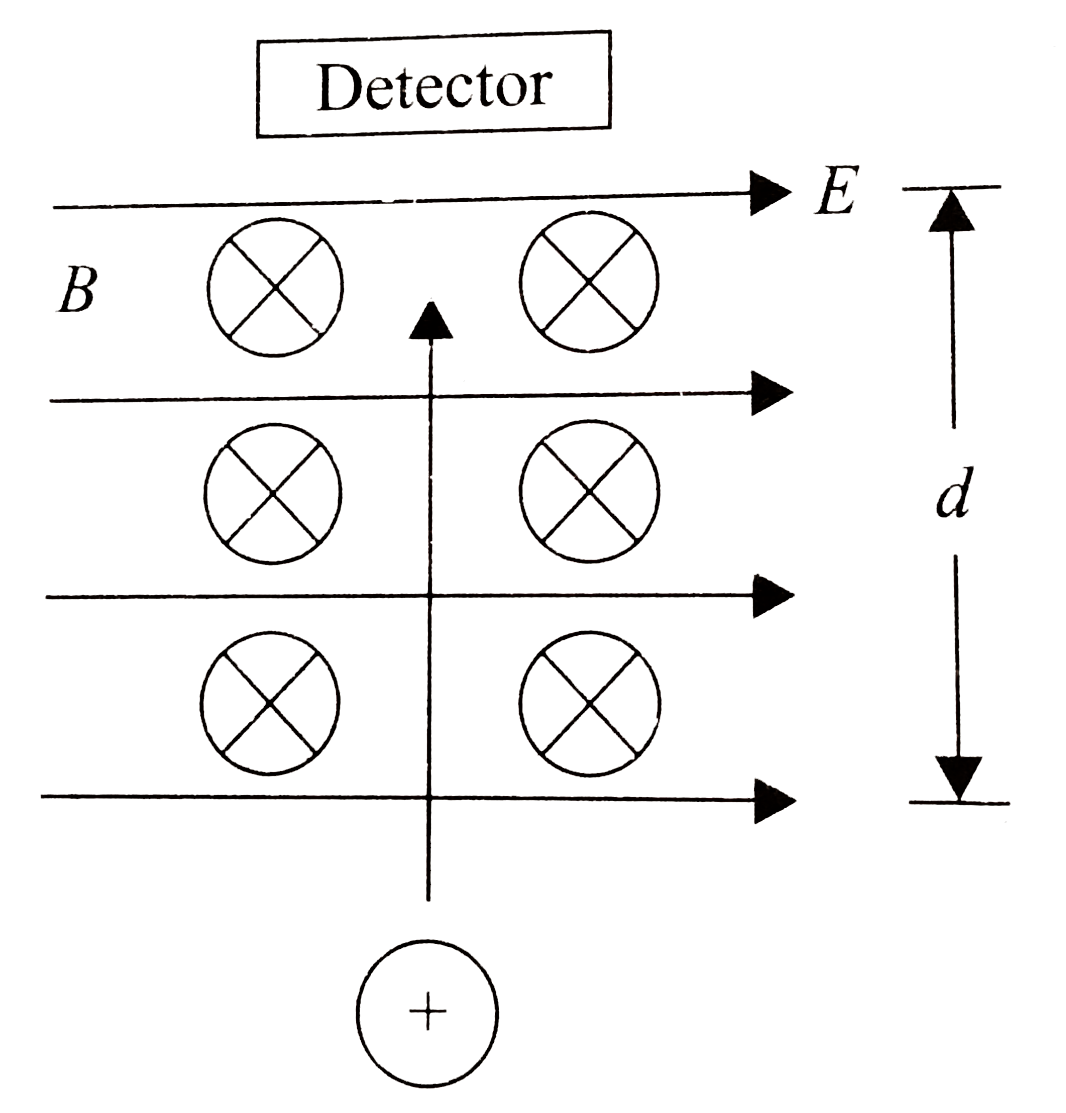
The moving particle will also experience a force due to magnetic field given by F = qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
If the filter is set to detect particles of speed v0, which one of the following diagrams best illustrates how the magnitude of the particle acceleration (a) depends on velocity v?
View SolutionAn electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other.
View SolutionThe path of a charged particle in a uniform magnetic field, when the velocity and the magnetic field are perpendicular to each other is a
View SolutionA charged particle is moved along a magnetic field line. The magnetic force on the particle is
View SolutionA charge q moves region in a electric field E and the magnetic field B both exist, then the force on its is
View SolutionIn a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
View SolutionA particle having charge q moves with a velocity v through a region in which both an electric field →E and a magnetic field B are present. The force on the particle is
View SolutionIf a charged particle at rest experiences no electromagnetic force, then electric field in that region
View SolutionA charged particle moving in a magnetic field experiences a resultant force
View SolutionIf a charged particle at rest experiences no electromagnetic force, then
The electric field must be zero
View Solution
