A beam of electrons having energy 28 keV each strikes a target generating X rays. The minimum wave length λmin (called cut off wavelength ) of the X rays generated is
4.4 nm
44 nm
0.044 nm
0.44 nm
The correct Answer is:C
To find the minimum wavelength (λ_min) of the X-rays generated when a beam of electrons strikes a target, we can use the following steps:
1. Understand the Energy of Electrons:
The energy of the electrons is given as 28 keV (kiloelectron volts). We need to convert this energy into electron volts (eV) for our calculations:
E=28 keV=28,000 eV
2. Use the Energy-Wavelength Relation:
The minimum wavelength of the X-rays can be calculated using the formula:
λmin=hcE
where:
- h is Planck's constant (6.626×10−34 J s)
- c is the speed of light (3×108 m/s)
- E is the energy in joules.
3. Convert Energy to Joules:
To use the formula, we need to convert the energy from eV to joules. The conversion factor is:
1 eV=1.602×10−19 J
Thus,
E=28,000 eV×1.602×10−19 J/eV=4.48×10−15 J
4. Substitute Values into the Formula:
Now we can substitute the values of h, c, and E into the formula for λmin:
λmin=(6.626×10−34 J s)(3×108 m/s)4.48×10−15 J
5. Calculate λmin:
Performing the calculation:
λmin=1.9878×10−25 J m4.48×10−15 J≈4.44×10−11 m
Converting meters to nanometers (1 m = 109 nm):
λmin≈0.0444 nm
6. Final Result:
Thus, the minimum wavelength (cut-off wavelength) of the X-rays generated is:
λmin≈0.044 nm
The energy of the electrons is given as 28 keV (kiloelectron volts). We need to convert this energy into electron volts (eV) for our calculations:
E=28 keV=28,000 eV
The minimum wavelength of the X-rays can be calculated using the formula:
λmin=hcE
where:
- h is Planck's constant (6.626×10−34 J s)
- c is the speed of light (3×108 m/s)
- E is the energy in joules.
To use the formula, we need to convert the energy from eV to joules. The conversion factor is:
1 eV=1.602×10−19 J
Thus,
E=28,000 eV×1.602×10−19 J/eV=4.48×10−15 J
Now we can substitute the values of h, c, and E into the formula for λmin:
λmin=(6.626×10−34 J s)(3×108 m/s)4.48×10−15 J
Performing the calculation:
λmin=1.9878×10−25 J m4.48×10−15 J≈4.44×10−11 m
Converting meters to nanometers (1 m = 109 nm):
λmin≈0.0444 nm
Thus, the minimum wavelength (cut-off wavelength) of the X-rays generated is:
λmin≈0.044 nm
Similar Questions
Knowledge Check
Electrons with de-Broglie wavelength λ fall on the target in an X-ray tube. The cut-off wavelength of the emitted X-ray is
Aλ0=2mcλ2hBλ0=2hmcCλ0=2m2c2λ2h2Dλ0=λ
An x-ray tube is operated at 20kV and the current through the tube is 0⋅5mA. Find (a) the number of electrons hitting the target per second, (b) the energy falling on the target per second as the kinetic energy of the electrons and © the cutoff wavelength of the X-rays emitted.
View SolutionThe intensity of X- ray from a coolidge tube is plotted againest wavelength λ as shown in the figure . The minimum wavelength found λc and the wavelength of theka line is λk, As the accelerating voliage is increase
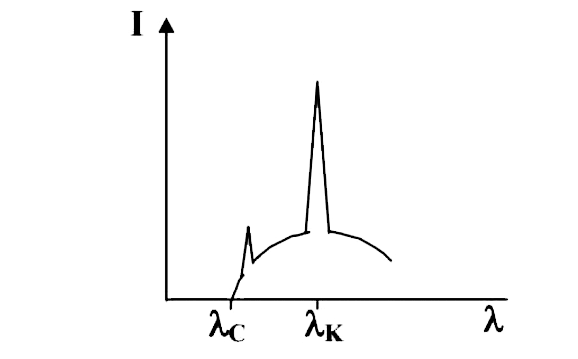
View SolutionThe intensity of X-rays form a Coolidge tube is plotted against wavelength λ as shown in the figure. The minimum wavelength found is λc and the wavelength of the Kα line is λk. As the accelerating voltage is increased
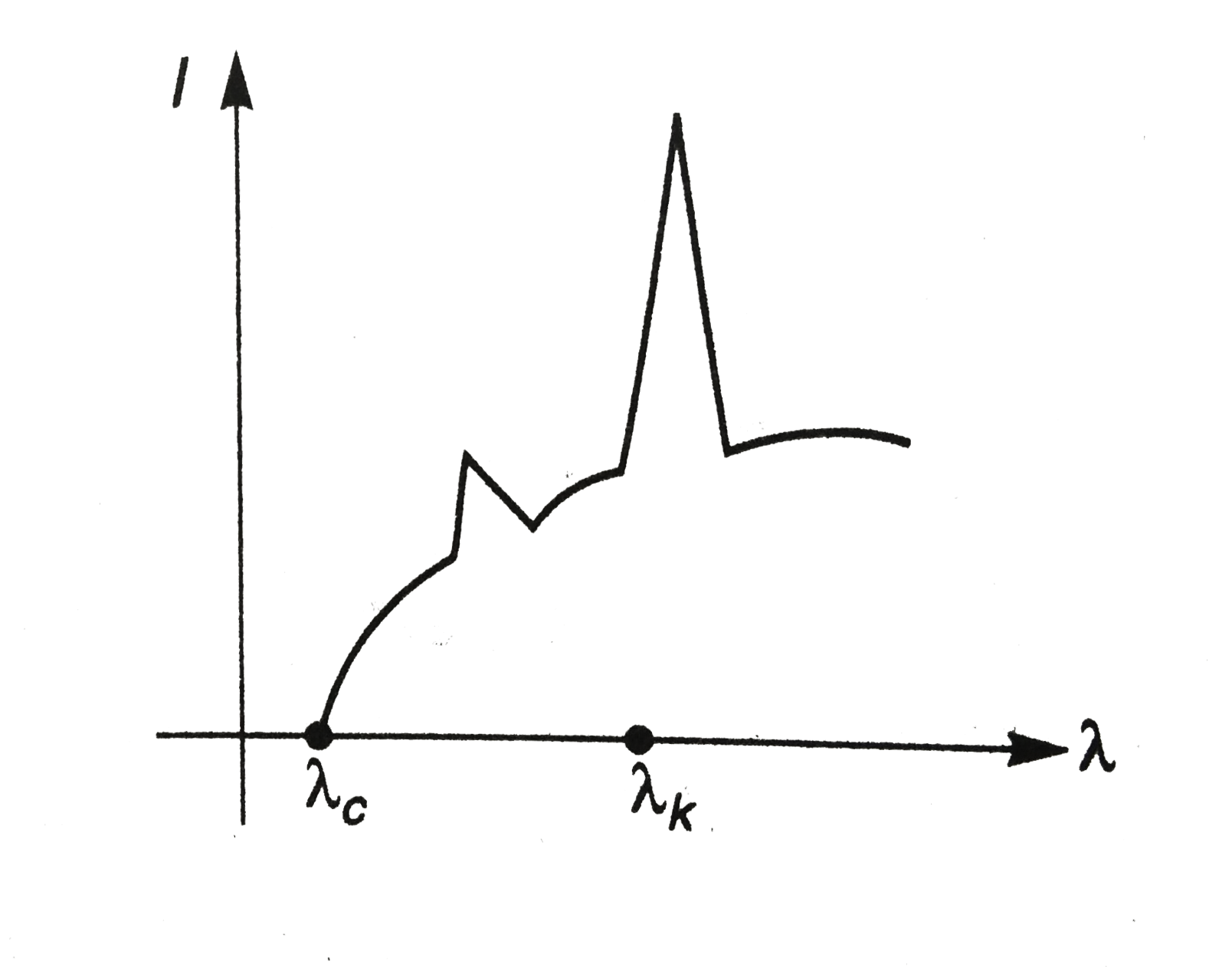
(a) λk−λc increases (b) λk−λc decreases
(c ) λk increases (d) λk decreases
View SolutionElectrons with de-Broglie wavelength λ fall on the target in an X-ray tube. The cut-off wavelength of the emitted X-ray is
View SolutionAn X-ray tube is operated at 20 kV. The cut off wavelength is
View SolutionA potential diffrence , the 20kv is applied across an X- ray s tube . The minimum wavelength of x- ray generated is …….Å .
View SolutionThe kinetic energy of electrons that strike the target is increased , then the cut-off wavelength of continuous X-rays spectrum
View Solution
