When the net force F acting on the particle varies as its position along x-axis shown in the figure, which of the following cannot be oscillatory motion. (where x is the position of the particle)

The correct Answer is:D
To determine which of the given force vs. position graphs cannot represent oscillatory motion, we need to analyze the relationship between force and displacement for each graph. In oscillatory motion, the force acting on the particle must always act in the opposite direction to the displacement from the equilibrium position. This means that when the displacement (x) is positive, the force (F) should be negative, and when the displacement is negative, the force should be positive.
1. Understand the Condition for Oscillatory Motion:
- For a particle to be in oscillatory motion, the force must always act in the opposite direction to the displacement. Mathematically, this can be expressed as:
F=−kx
- Here, k is a positive constant, and F and x must have opposite signs.
2. Analyze Each Graph:
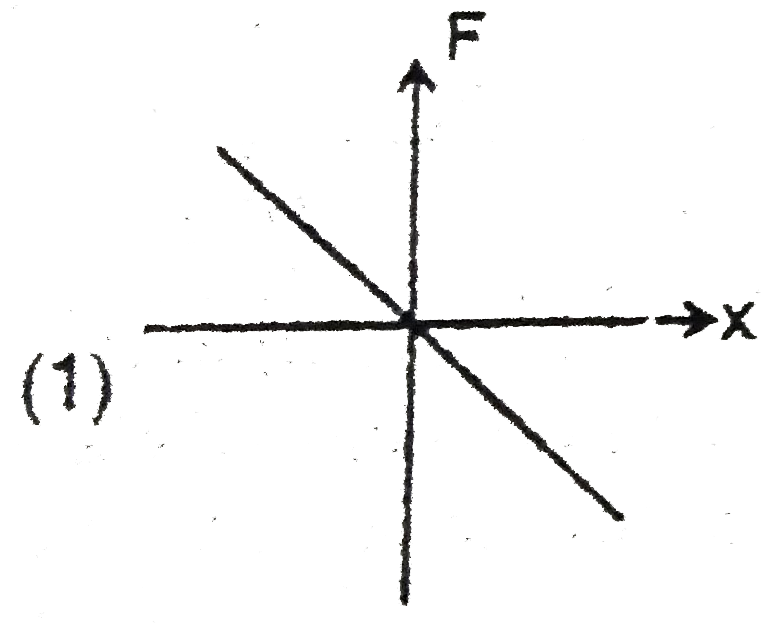
- Graph 1: Check the relationship between force and displacement.
- If x<0 (negative), then F>0 (positive).
- If x>0 (positive), then F<0 (negative).
- This graph satisfies the condition for oscillatory motion.
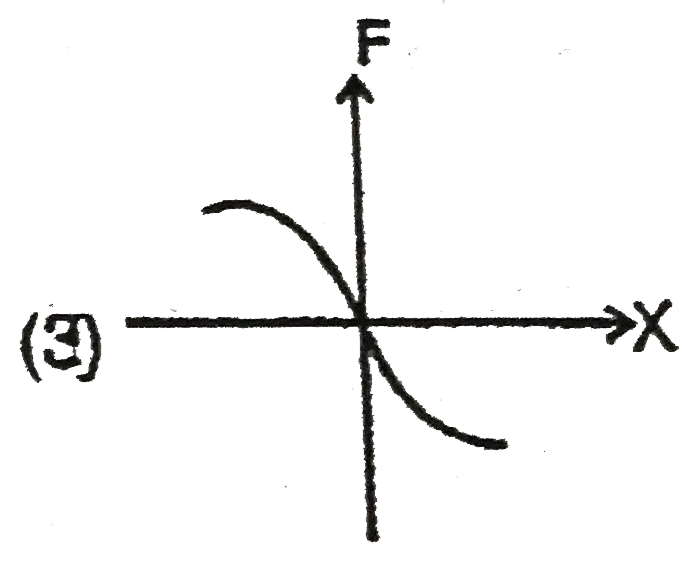
- Graph 2: Check the relationship.
- If x<0, then F>0.
- If x>0, then F<0.
- This graph also satisfies the condition for oscillatory motion.
- Graph 3: Check the relationship.
- If x<0, then F>0.
- If x>0, then F<0.
- This graph satisfies the condition for oscillatory motion as well.
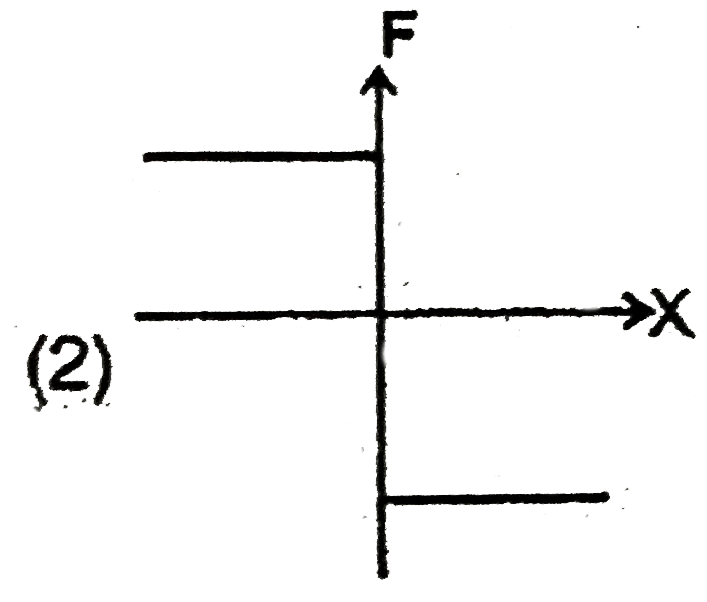
- Graph 4: Check the relationship.
- If x<0, then F<0 (negative).
- If x>0, then F>0 (positive).
- This graph does not satisfy the condition for oscillatory motion since the force and displacement are in the same direction for both positive and negative displacements.
3. Conclusion:
- The graph that cannot represent oscillatory motion is Graph 4 because the force does not act in the opposite direction to the displacement.
Final Answer:
The graph that cannot represent oscillatory motion is Graph 4.
- For a particle to be in oscillatory motion, the force must always act in the opposite direction to the displacement. Mathematically, this can be expressed as:
F=−kx
- Here, k is a positive constant, and F and x must have opposite signs.
- Graph 1: Check the relationship between force and displacement.
- If x<0 (negative), then F>0 (positive).
- If x>0 (positive), then F<0 (negative).
- This graph satisfies the condition for oscillatory motion.
- If x<0, then F>0.
- If x>0, then F<0.
- This graph also satisfies the condition for oscillatory motion.
- If x<0, then F>0.
- If x>0, then F<0.
- This graph satisfies the condition for oscillatory motion as well.
- If x<0, then F<0 (negative).
- If x>0, then F>0 (positive).
- This graph does not satisfy the condition for oscillatory motion since the force and displacement are in the same direction for both positive and negative displacements.
- The graph that cannot represent oscillatory motion is Graph 4 because the force does not act in the opposite direction to the displacement.
The graph that cannot represent oscillatory motion is Graph 4.
Topper's Solved these Questions
Similar Questions
A force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionThe variation of force (F) acting on a particle of mass 800 g with position (x) is as shown in figure. The time period of oscillation of the particles is
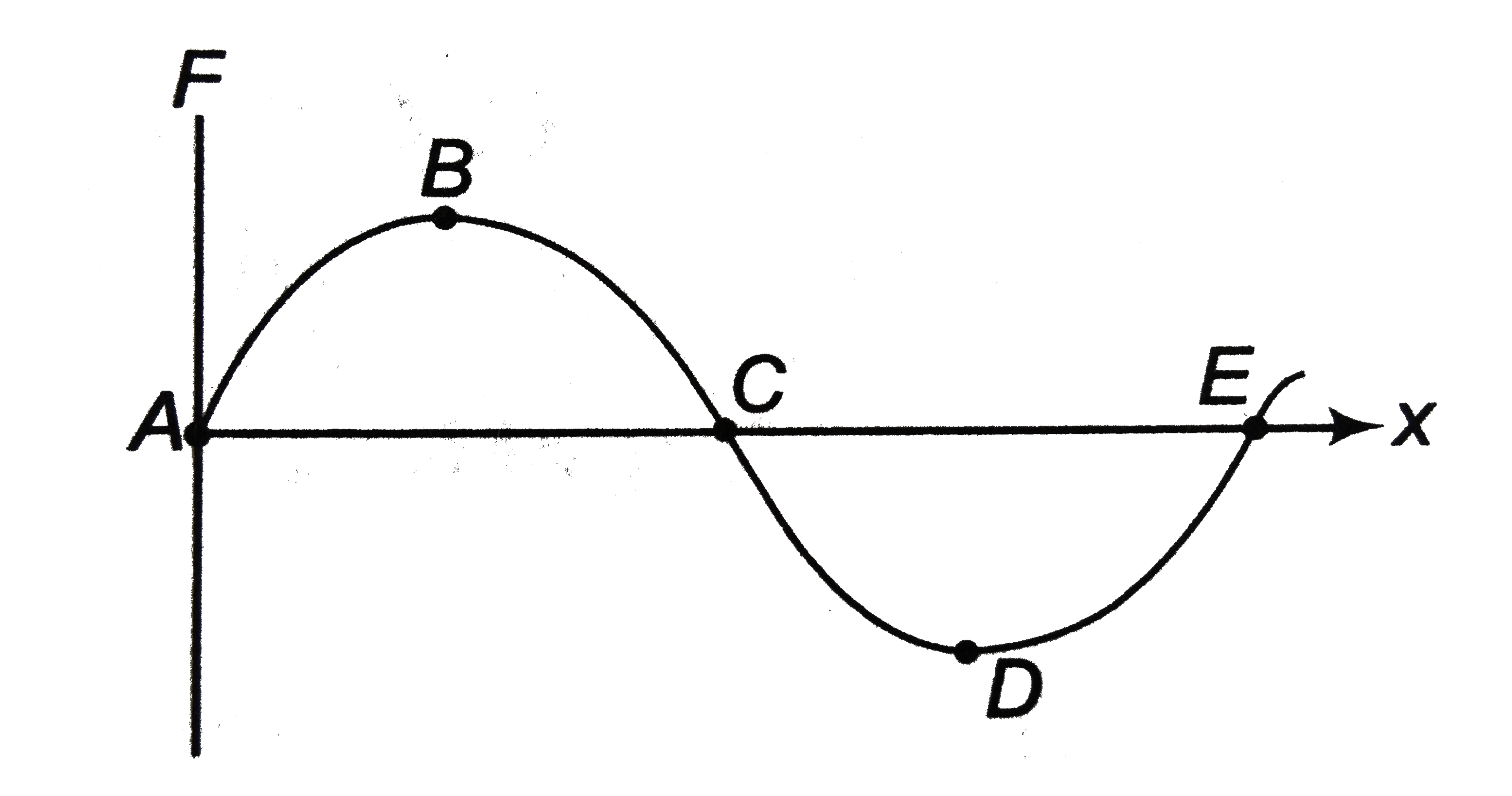
View SolutionForce acting on a particle moving along x-axis as shown in figure. Find points of stable and unstable equlibrium.
 .
.
View SolutionA position dependent force F acting on a particle and its force-position curve is shown in the figure. The work done by force from x=1 m to x=4 m is
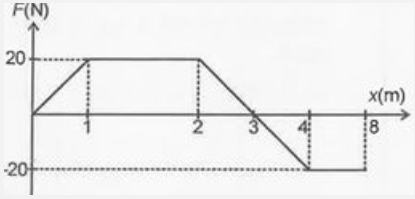
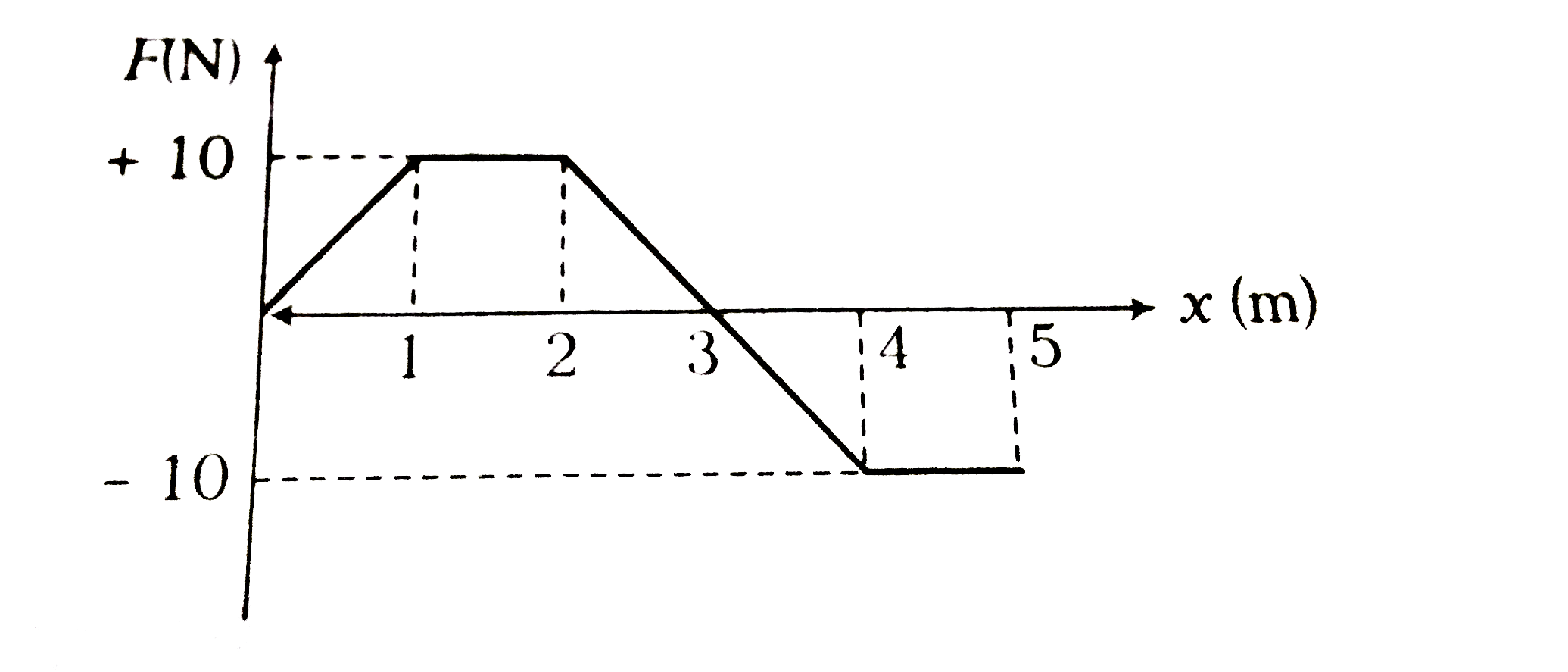
View SolutionA position dependent force F ia acting on a particle and its force-position curve is shown in the figure. Work done on the particle, when its displacement is from 0 to 5 m is
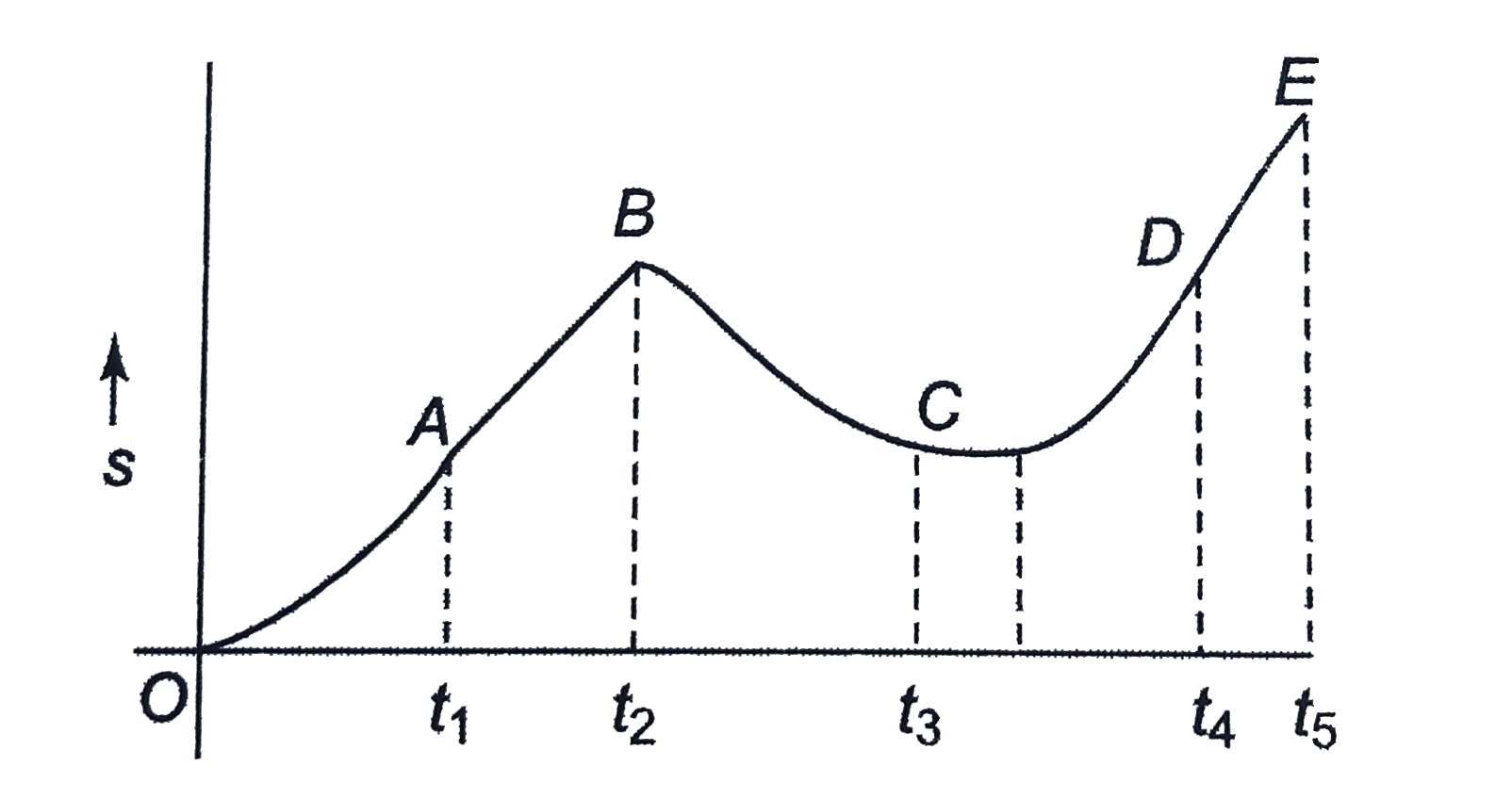
View SolutionA particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
View SolutionThe acceleration of a particle which moves along the positive x-axis varies with its position as shown in figure. If the velocity of the particle is 0.8ms−1 at x = 0, then velocity of the particle at x=1.4m is (∈ms−1).
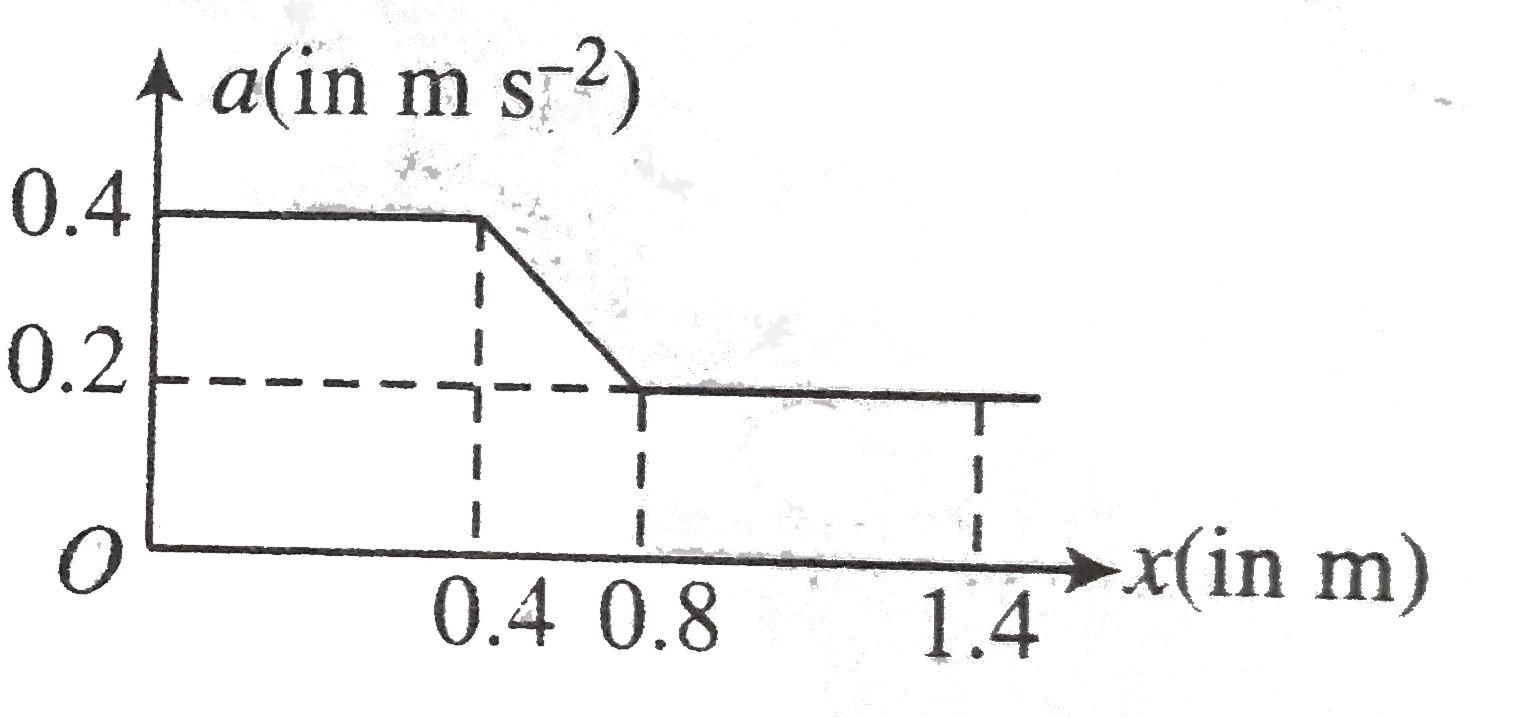
View SolutionThe net force acting on a particle moving along a straight line varies with time as shown in the diagram. Force is parallel to velocity. Which of the following graph is best representative of its speed with time? (Initial velocity of the particle is zero)

View SolutionIn the figure shown the potential energy U of a particle is plotted its position 'x' from origin. Then which of the following statement is correct A particle at :

View SolutionA time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View Solution
