A time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
The correct Answer is:D
To solve the problem step by step, we will use the impulse-momentum theorem, which states that the impulse applied to an object is equal to the change in its momentum.
1. Identify the Given Values:
- Time-varying force: F(t)=2t
- Mass of the particle: m=2kg
- Initial velocity at t=0: v0=−4m/s (negative indicates direction along the negative x-axis)
- Time interval: t=4s
2. Calculate the Impulse:
- Impulse J is given by the integral of force over time:
J=∫40F(t)dt=∫402tdt
- Evaluating the integral:
J=2∫40tdt=2(t22)40=2(422−022)=2(162)=2×8=16Ns
3. Relate Impulse to Change in Momentum:
- The change in momentum Δp is given by:
J=Δp=m(vf−v0)
- Substituting the known values:
16=2(vf−(−4))
- Simplifying:
16=2(vf+4)
8=vf+4
vf=8−4=4m/s
4. Final Result:
- The final velocity of the particle at t=4s is vf=4m/s.
- Time-varying force: F(t)=2t
- Mass of the particle: m=2kg
- Initial velocity at t=0: v0=−4m/s (negative indicates direction along the negative x-axis)
- Time interval: t=4s
- Impulse J is given by the integral of force over time:
J=∫40F(t)dt=∫402tdt
- Evaluating the integral:
J=2∫40tdt=2(t22)40=2(422−022)=2(162)=2×8=16Ns
- The change in momentum Δp is given by:
J=Δp=m(vf−v0)
- Substituting the known values:
16=2(vf−(−4))
- Simplifying:
16=2(vf+4)
8=vf+4
vf=8−4=4m/s
- The final velocity of the particle at t=4s is vf=4m/s.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 11videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples13videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
Force acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
 View Solution
View SolutionA 2kg toy car can move along an x axis. Graph shows force Fx , acting on the car which being at rest at time t=0 . The velocity of the particle at t=10s is:
 View Solution
View SolutionIf the velocity of a paraticle moving along x-axis is given as v=(4t2+3t=1)m/s then acceleration of the particle at t=1sec is :
View SolutionThe displacement x of a particle moving along x-axis at time t is given by x2=2t2+6t. The velocity at any time t is
View SolutionThe magnitude of force acting on a particle moving along x-axis varies with time (t) as shown in figure. If at t = 0 the velocity of particle is v0, then its velocity at t=T0 will be
 View Solution
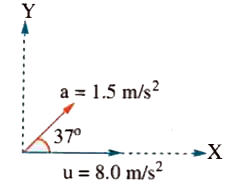
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
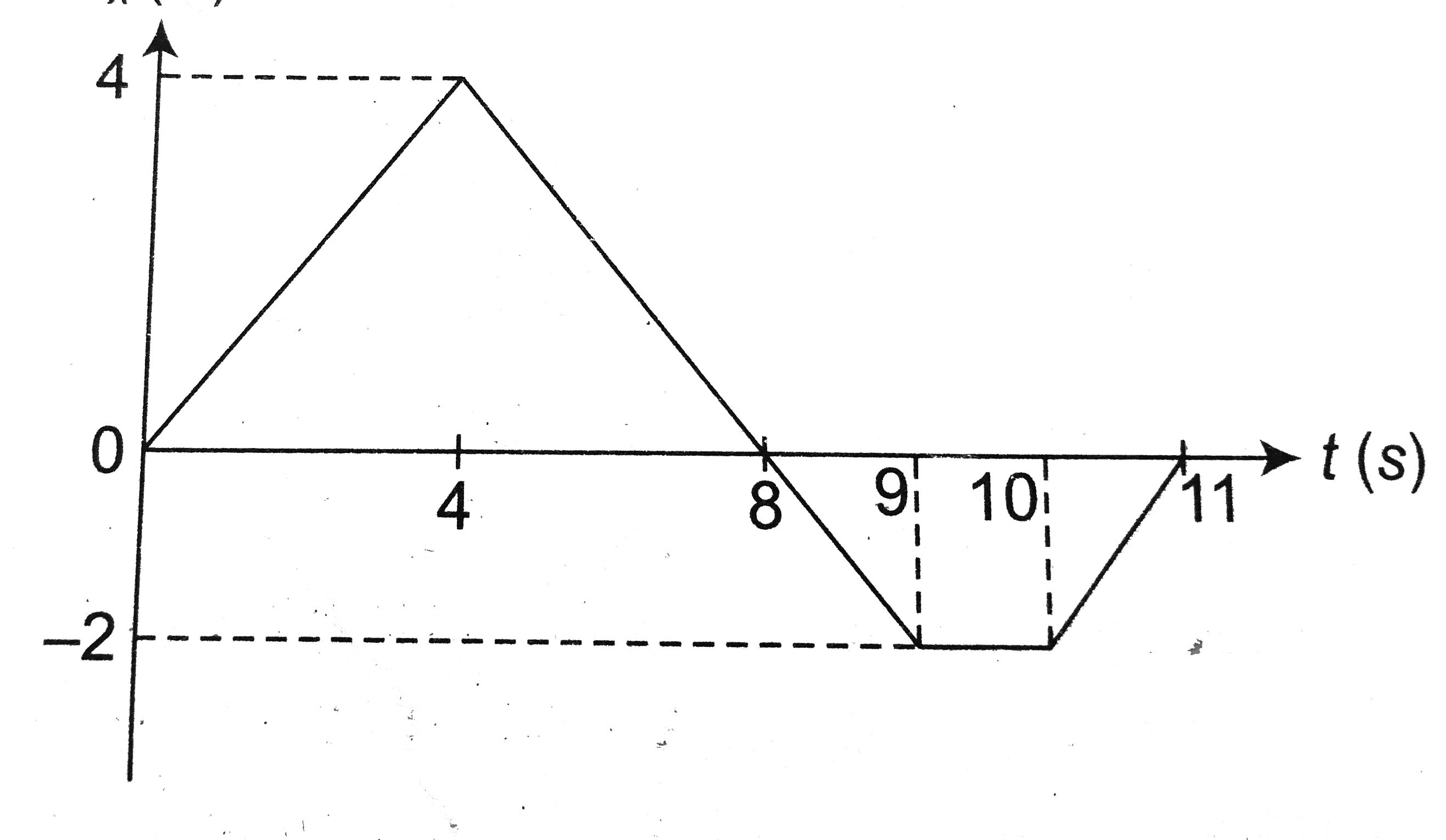
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.View SolutionThe position (X)-time (t) graph for a particle of mass 1 kg moving along x-axis is shown in figure. Find impulse on particle at t = 4 s.
 View Solution
View SolutionThe position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View Solution

