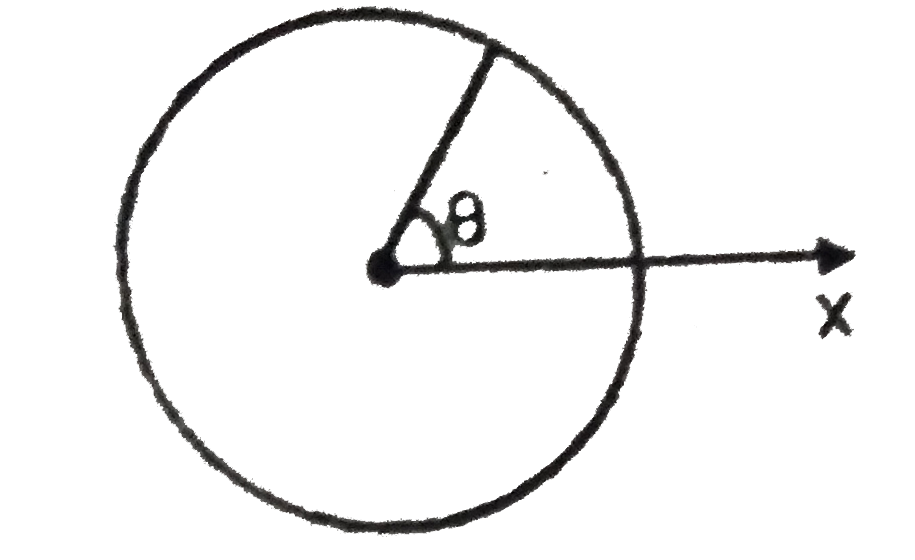
The linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
a.0
b.λ0∈0
c.λ0π∈0
d.λ02π∈0
The correct Answer is:A
All the charges are at a distance R.
∴V=kqnetR=0
Topper's Solved these Questions
Similar Questions
The linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionA circle of radius a has charge density given by λ=λ0cos2θ on its circumference, where λ0 is a positive constant and θ is the angular position of a point on the circle with respect to some reference line. The potential at the centre of the circle is
View SolutionCharge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimuthal angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.
View SolutionThe given two fixed rings of radius R lie in XY plane as shown in the figure. Linear charge density of the rings A and B varies as per the relationλ=λ0sinθ and λ=λ0cosθ respectively where theta is measured from +x axis. Distance between the centre of the two rings is r>>R
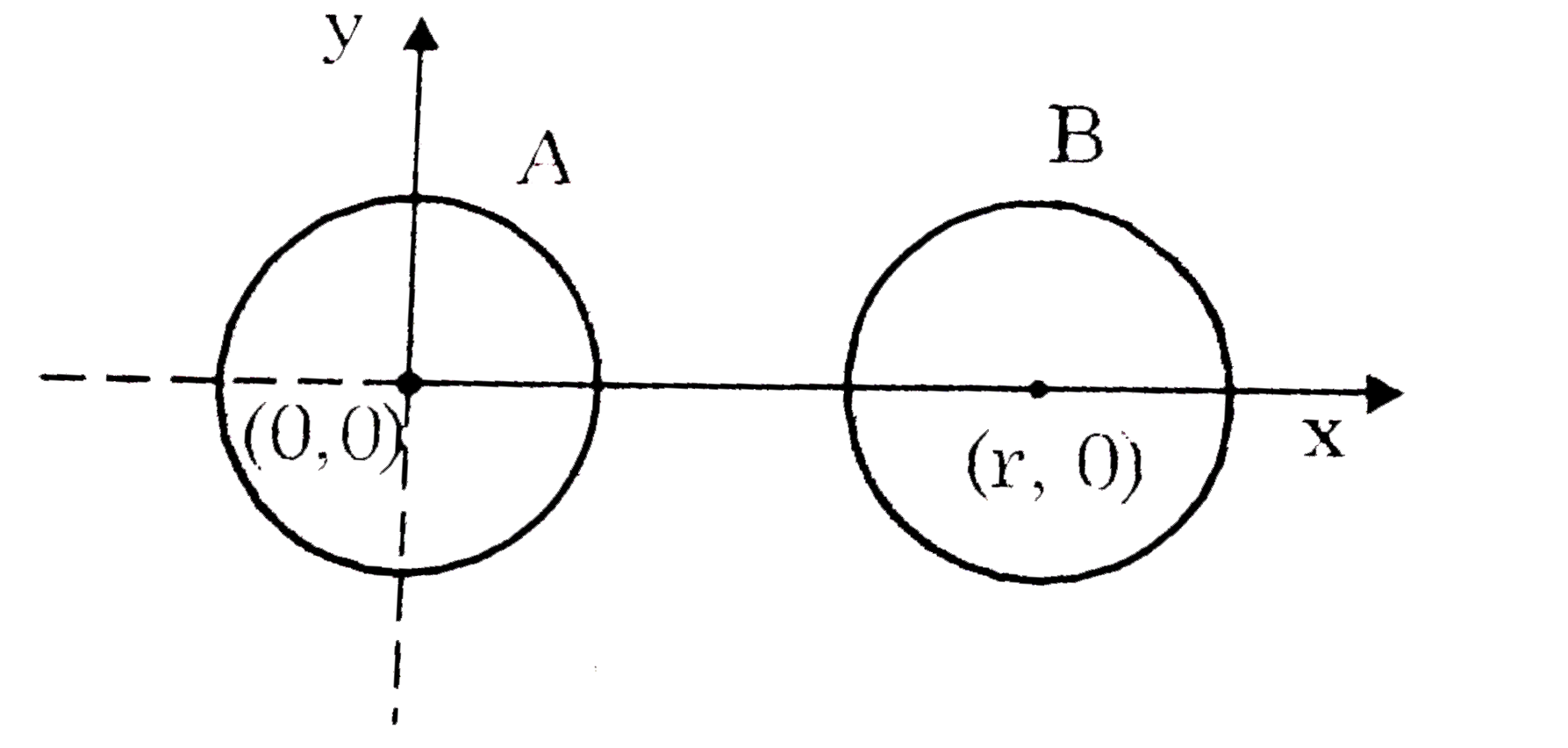
View SolutionThe linear charge density on upper half of semi-circular section of ring is λ and that at lower half is −λ. The direction of electric field at centre O of ring is :

View SolutionA semicircular ring of radius 0.5 m is uniformly charged with a total charge of 1.5×10−9 coul. The electric potential at the centre of this ring is :
View SolutionA uniformly charged ring of radius R is rotated about its axis with constant linear speed v of each of its particle. The ratio of electric field to magnetic field at a point P on the axis of the ring distant x=R from centre of ring is (c is speed of light )

View SolutionConsider a uniformly charged ring of radius R. Find the point on the axis where the electric field is maximum.
View Solution