One end of ideal string tied up with fixed suppot & other end is tied with a bob. The string is released from horizontal position. When string makes an angle of θ with vertically downward direction then the acceleration vector of bob is horizontal then θ is
tan−1(2)
tan−1(1/2)
tan−1(√3)
tan−1(√2)
To solve the problem, we need to analyze the motion of the bob attached to the string and determine the angle θ when the acceleration vector of the bob is horizontal.
1. Understanding the Setup:
- The bob is attached to a string that is fixed at one end. The other end is released from a horizontal position.
- As the bob swings down, it makes an angle θ with the vertical.
2. Identifying Forces:
- The forces acting on the bob are its weight mg acting downward and the tension T in the string acting along the string.
- At the angle θ, the weight can be resolved into two components:
- A component along the direction of the string: mgcosθ
- A component perpendicular to the string (tangential): mgsinθ
3. Acceleration Components:
- The acceleration of the bob can also be resolved into two components:
- Tangential acceleration at along the path of the bob: at=gsinθ
- Centripetal acceleration ac directed towards the center of the circular path: ac=V2L where V is the speed of the bob and L is the length of the string.
4. Condition for Horizontal Acceleration:
- The problem states that the acceleration vector of the bob is horizontal. This means that the tangential acceleration must equal the centripetal acceleration:
gsinθ=V2L
5. Finding the Velocity:
- To find V, we can use the work-energy principle. The work done by gravity as the bob moves from the horizontal position to the angle θ is equal to the change in kinetic energy:
Work done=mg⋅(L−Lcosθ)=mgL(1−cosθ)
- This work done equals the kinetic energy gained:
mgL(1−cosθ)=12mv2
- Simplifying gives:
v2=2gL(1−cosθ)
6. Substituting for V2:
- Substitute V2 back into the equation for acceleration:
gsinθ=2gL(1−cosθ)L
- This simplifies to:
sinθ=2(1−cosθ)
7. Using Trigonometric Identity:
- Using the identity 1−cosθ=sin2θ2:
sinθ=2sin2θ2
- Let x=sinθ2, then sinθ=2x(1−x2).
8. Finding θ:
- Solving the equation sinθ=2(1−cosθ) leads to:
sinθ=2sin2θ2
- This gives us tan2θ=2, hence tanθ=√2.
9. Final Result:
- Therefore, the angle θ is:
θ=tan−1(√2)
- The bob is attached to a string that is fixed at one end. The other end is released from a horizontal position.
- As the bob swings down, it makes an angle θ with the vertical.
- The forces acting on the bob are its weight mg acting downward and the tension T in the string acting along the string.
- At the angle θ, the weight can be resolved into two components:
- A component along the direction of the string: mgcosθ
- A component perpendicular to the string (tangential): mgsinθ
- The acceleration of the bob can also be resolved into two components:
- Tangential acceleration at along the path of the bob: at=gsinθ
- Centripetal acceleration ac directed towards the center of the circular path: ac=V2L where V is the speed of the bob and L is the length of the string.
- The problem states that the acceleration vector of the bob is horizontal. This means that the tangential acceleration must equal the centripetal acceleration:
gsinθ=V2L
- To find V, we can use the work-energy principle. The work done by gravity as the bob moves from the horizontal position to the angle θ is equal to the change in kinetic energy:
Work done=mg⋅(L−Lcosθ)=mgL(1−cosθ)
- This work done equals the kinetic energy gained:
mgL(1−cosθ)=12mv2
- Simplifying gives:
v2=2gL(1−cosθ)
- Substitute V2 back into the equation for acceleration:
gsinθ=2gL(1−cosθ)L
- This simplifies to:
sinθ=2(1−cosθ)
- Using the identity 1−cosθ=sin2θ2:
sinθ=2sin2θ2
- Let x=sinθ2, then sinθ=2x(1−x2).
- Solving the equation sinθ=2(1−cosθ) leads to:
sinθ=2sin2θ2
- This gives us tan2θ=2, hence tanθ=√2.
- Therefore, the angle θ is:
θ=tan−1(√2)
Similar Questions
A bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
View SolutionIn a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle θ with the vertical.
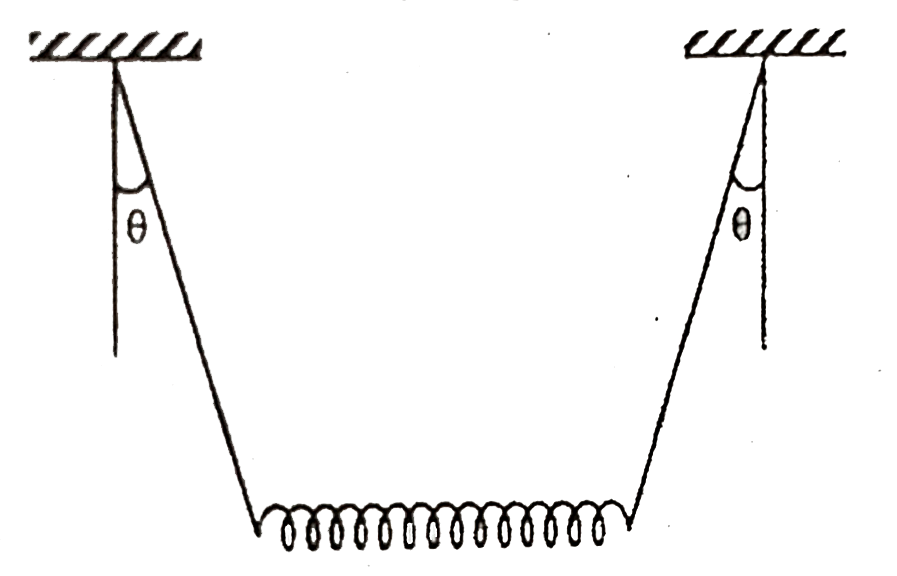
View SolutionA spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle θ with the vertical. The extension of the spring is.
View SolutionA bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle 37∘ with the vertical. Find the acceleration of the trolley.

View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View SolutionA block of mass m can slide freely in a slot made in a bigger of mass M as shown in fig. There is no friction anywhere in the system.

The block m is connected to one end of a string whose other end is fixed at point P. system is released from rest when the string at P makes an angle θ with horizontal. Find the acceleration of m and M after release.
View SolutionA simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View Solution
