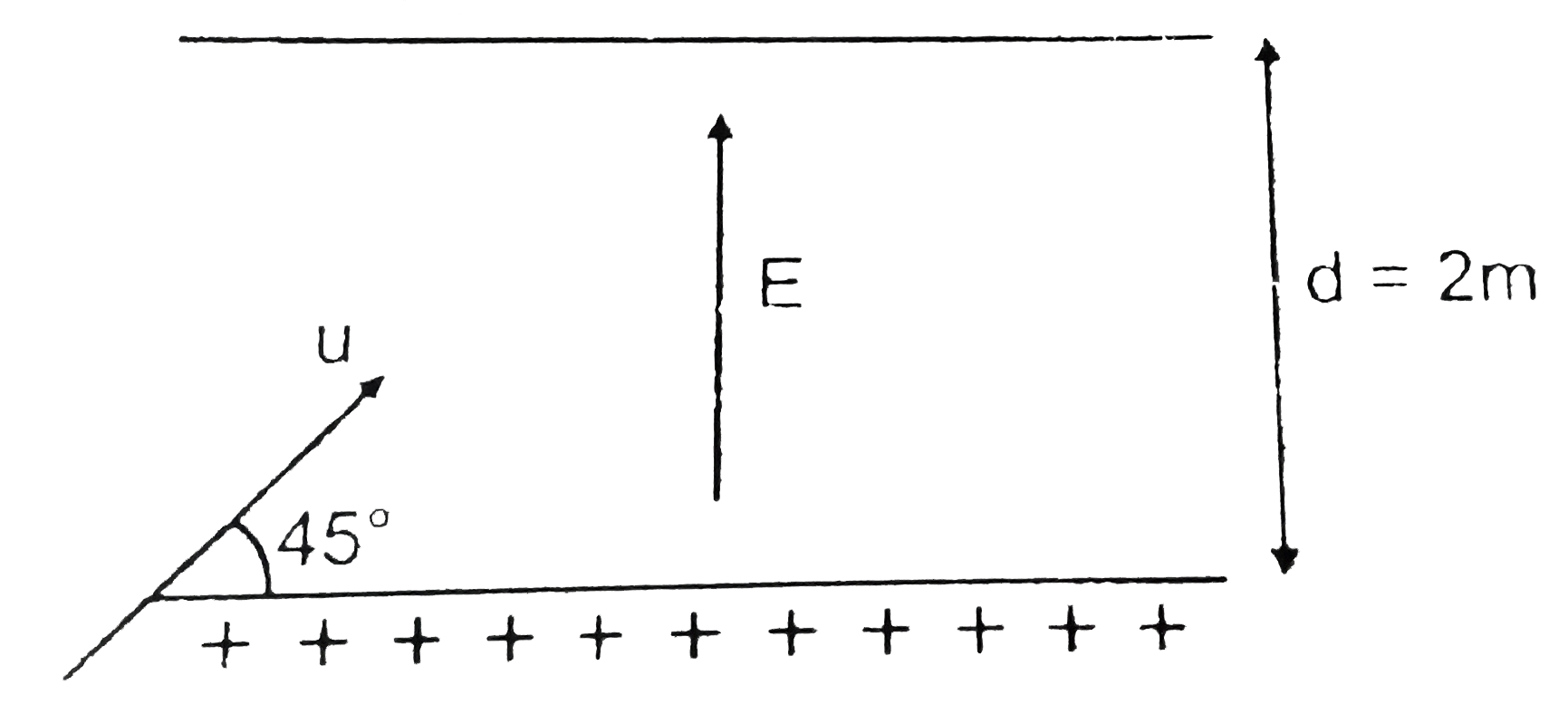
An electron is projected as shown with speed u. If electron just fails to strike the upper plate, find range. (distance from starting point at which electron strike the lower plate again). Consider only electric force.
The correct Answer is:8
ucosθ×t=R .(1)
⏐⏐
⏐
⏐↓a=(qEm)
(u√2)=(qEm)t2⇒t=2μ√2qE .(2)
(u√2)2=2(qEm)dimpliesqEm2=u24d ..(3)
⇒t=2u√2u2(4d)=4√2du
put in (1)
R=(u√2)(4√2du)=4d
Similar Questions
An electron is projected as shown in fig. with kinetic energy K, at an angle θ=45∘ between two charged plates. Ignore the gravity.
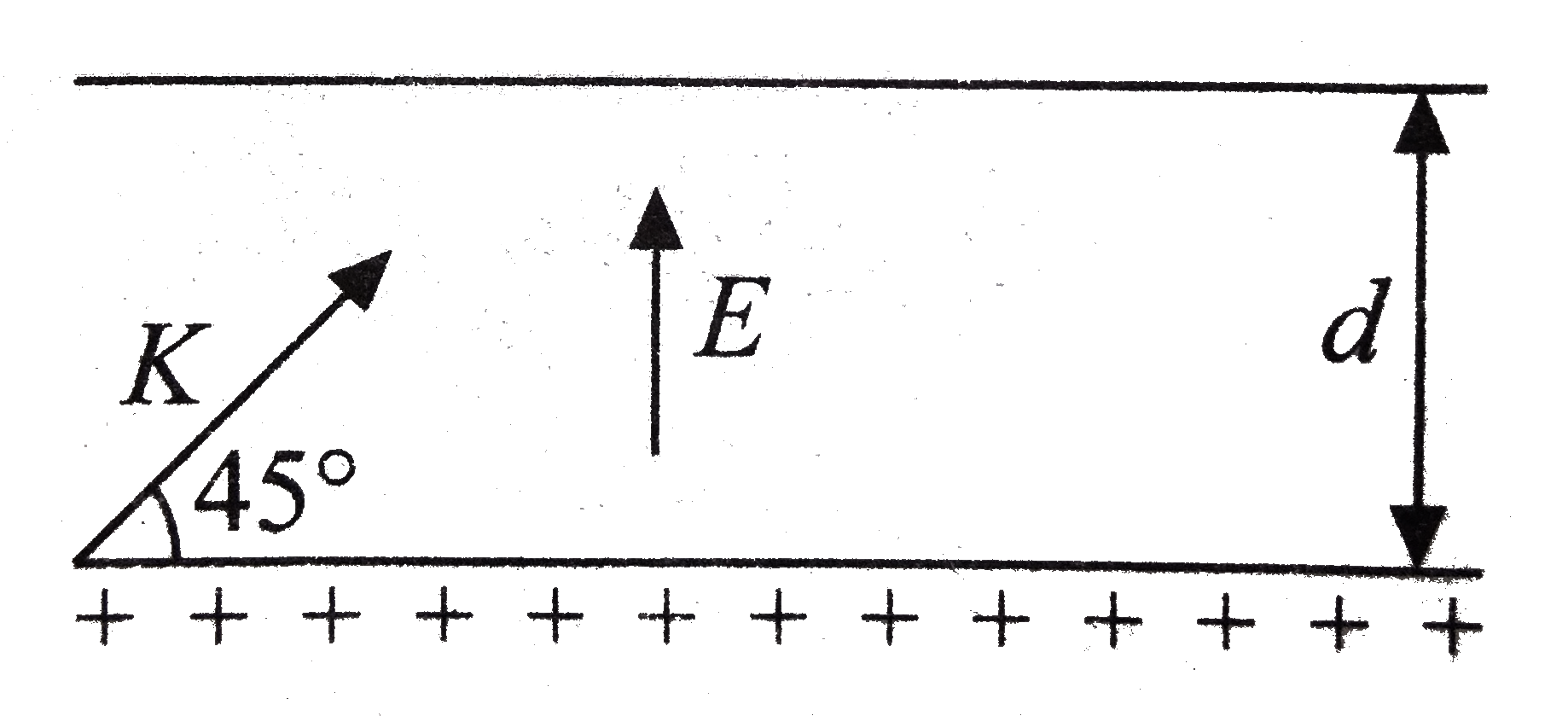
At what distance from the starting point will the electron strike the lower plate?View SolutionBoth the capacitors shown in figure are made of square plates of edge a. The separatiopn between the plates of the capacitors are d1andd2 as shown in the figure. A potential difference V is applied between the points a and b. An electron is projected between the plates of the upper capacitor along the central line. With what minimum speed should the electron be projected so that it does not collide with any plate ? Consider only the electric forces.
 View Solution
View SolutionAn electron is projected as in figure with kinetic energy K, at an angle θ=45∘ between two charged plates. The magnitude of the electric field so that the electron just fails to strike the upper plate, should be greater than:
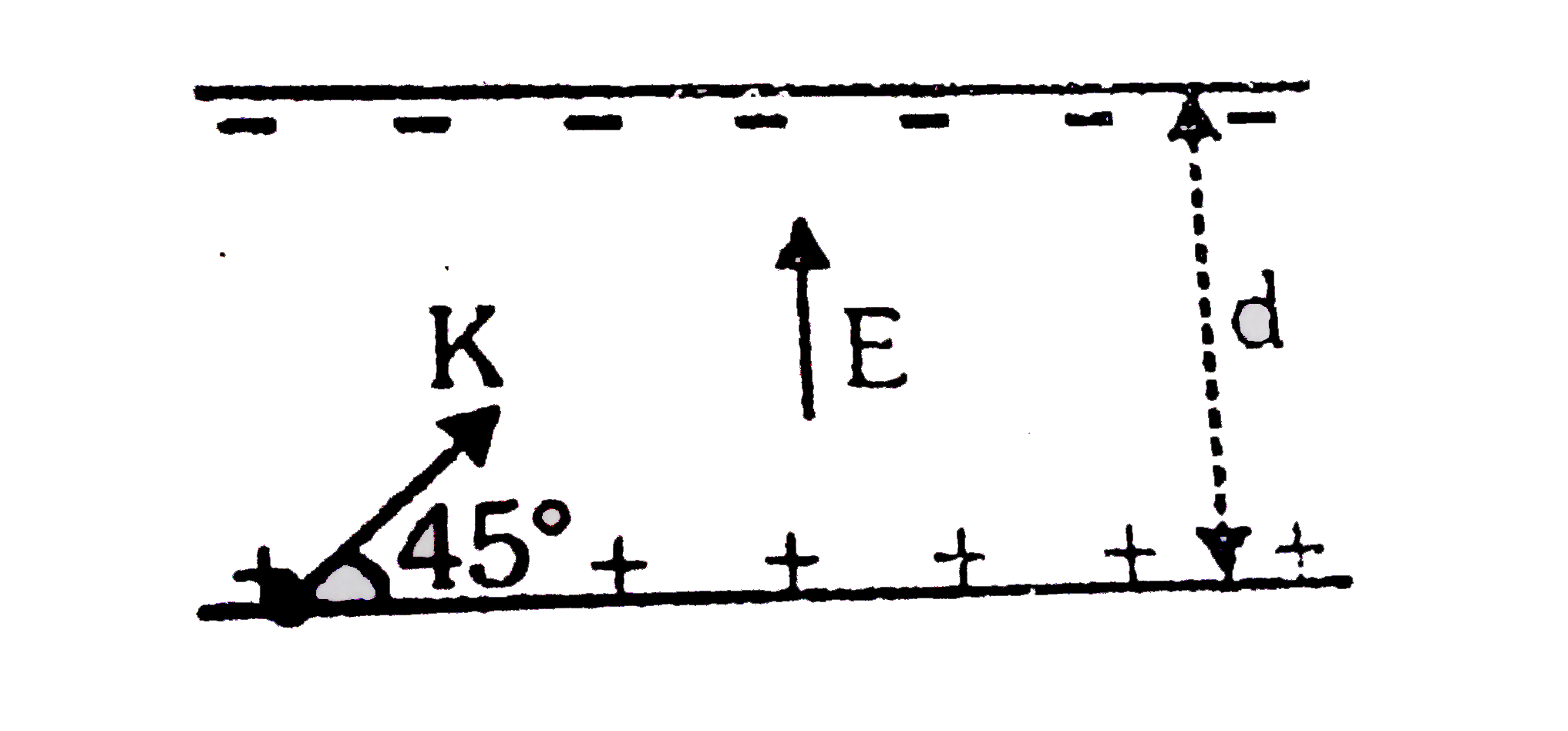 View Solution
View SolutionAn electric field of magnitude 1000NC−1 is produced between two parallel platees having a separation of 2.0 cm as shown in figure(29.E4) (a) What is the potential difference between the plates? (b) With what minimum speed should an electron be projected from the lower plate in the direction of the field so that it may reach the upper plate? ( c) Suupose the electron is projected from the lower plate with the speed calculated in part (b) . The direction of projection makes an angle of 60∘ with the field. Find the mazimum height reached by the electron.
 View Solution
View SolutionTwo charged metal plates in vacuum are 10cm apart. A uniform electric field of intensity (45/16)×103NC−1 is applied between the plates. An electron is released between the plates from rest at a point just outside the negative plate.
(a) Calculate how long (t) will the electron take to reach the other plate?
(b) At what velocity (v) will it be electron take to hits teh other plate?View SolutionIn Fig. what should be the speed of the charged particle so that it cannot collide with the upper wall? Also, find the coordinates of the point where the particle strikes the lower plate in the limiting case of velocity.
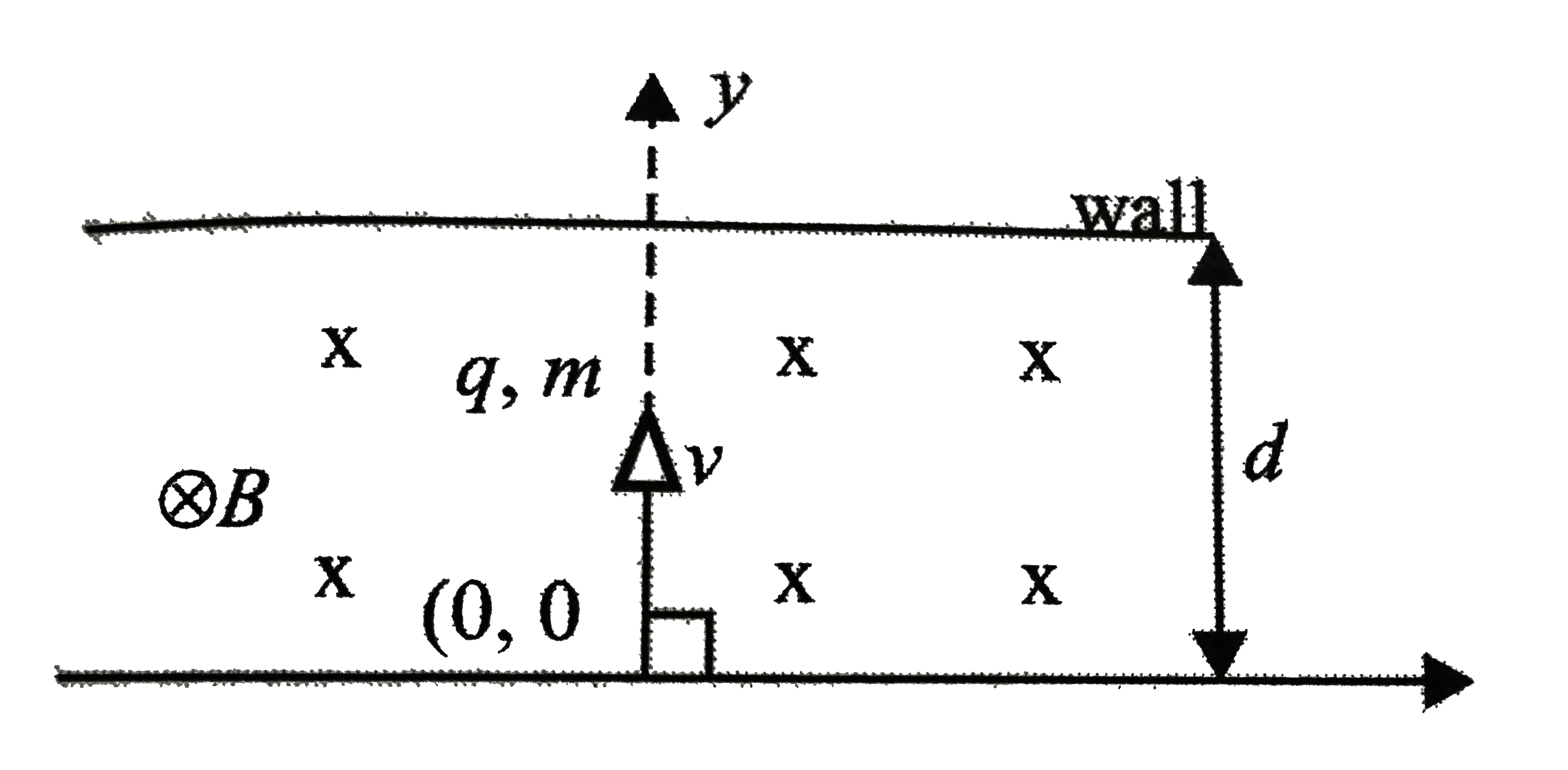 View Solution
View SolutionIn Fig. what should be the speed of the charged particle so that it cannot collide with the upper wall? Also, find the coordinates of the point where the particle strikes the lower plate in the limiting case of velocity.
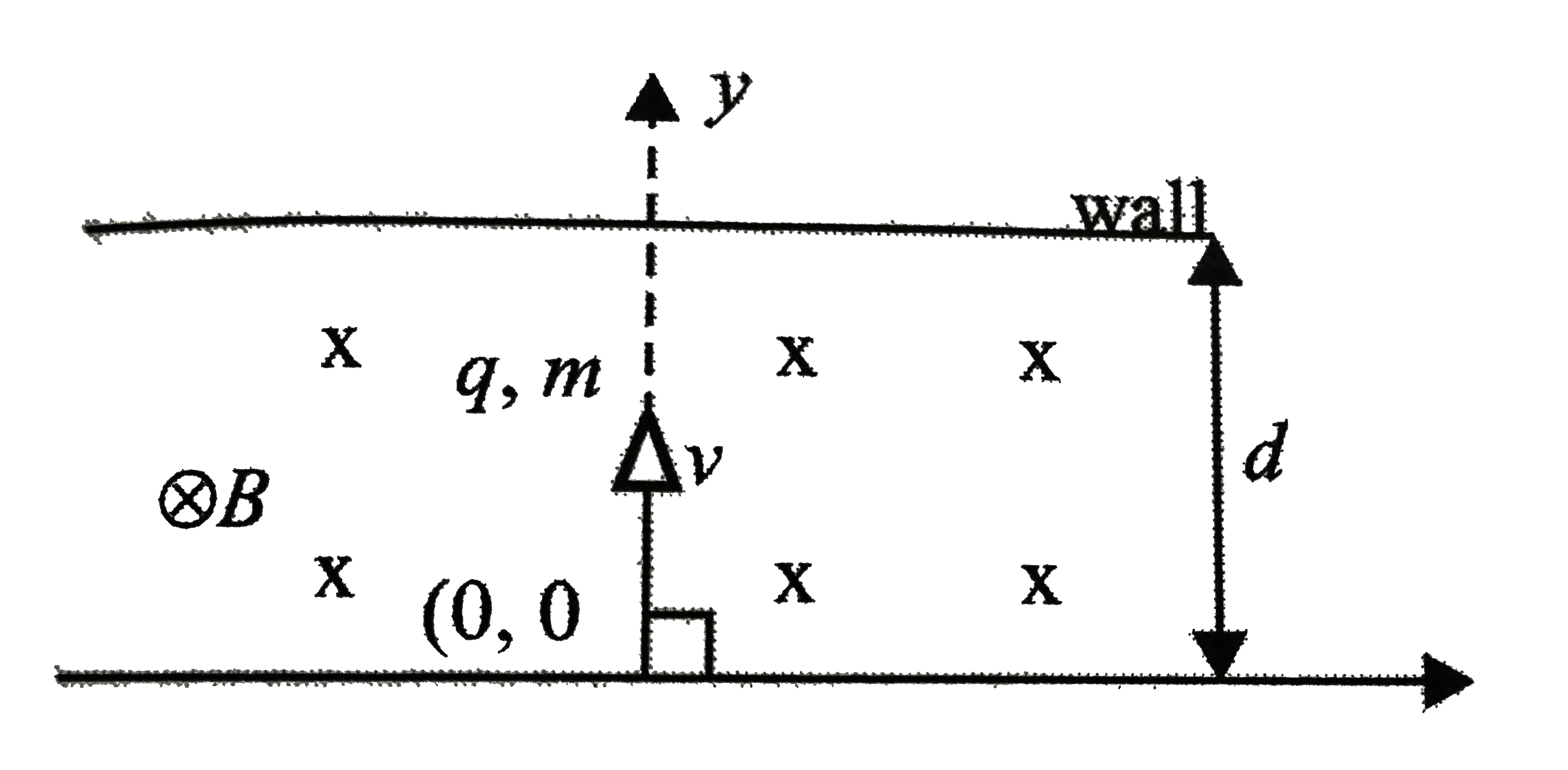 View Solution
View SolutionA man of mass M=58kg jumps from an aeroplane as shown in Fig. He sees the hard ground below him and a lake at a distance d=1m from the point directly below him. He immediately puts off his jacket (mass m=2 kg) and throws it in a direction directly away from the lake. If he just fails to strike the ground, find the distance (in 101m) he should walk now to pick his jacket. (Neglect air resistance and take the velocity of man at the time of jump with respect to earth zero.)
 View Solution
View SolutionBoth the capacitors shown in figure are made of square plates of edge a . The separations between the plates of the capacitors and d1 and d2 as shown in the figure. A battery of V volt and a resistance R are connected as shown in figure. At steady state an electron is projected between the plates of the lower capacitor from its lower plate along the plate as shown. Minimum speed should the electron be projected is given by 1√n(Vea2md2)1/2 so that it does not collide with any plate? Consider only the electric forces then find the value of n.
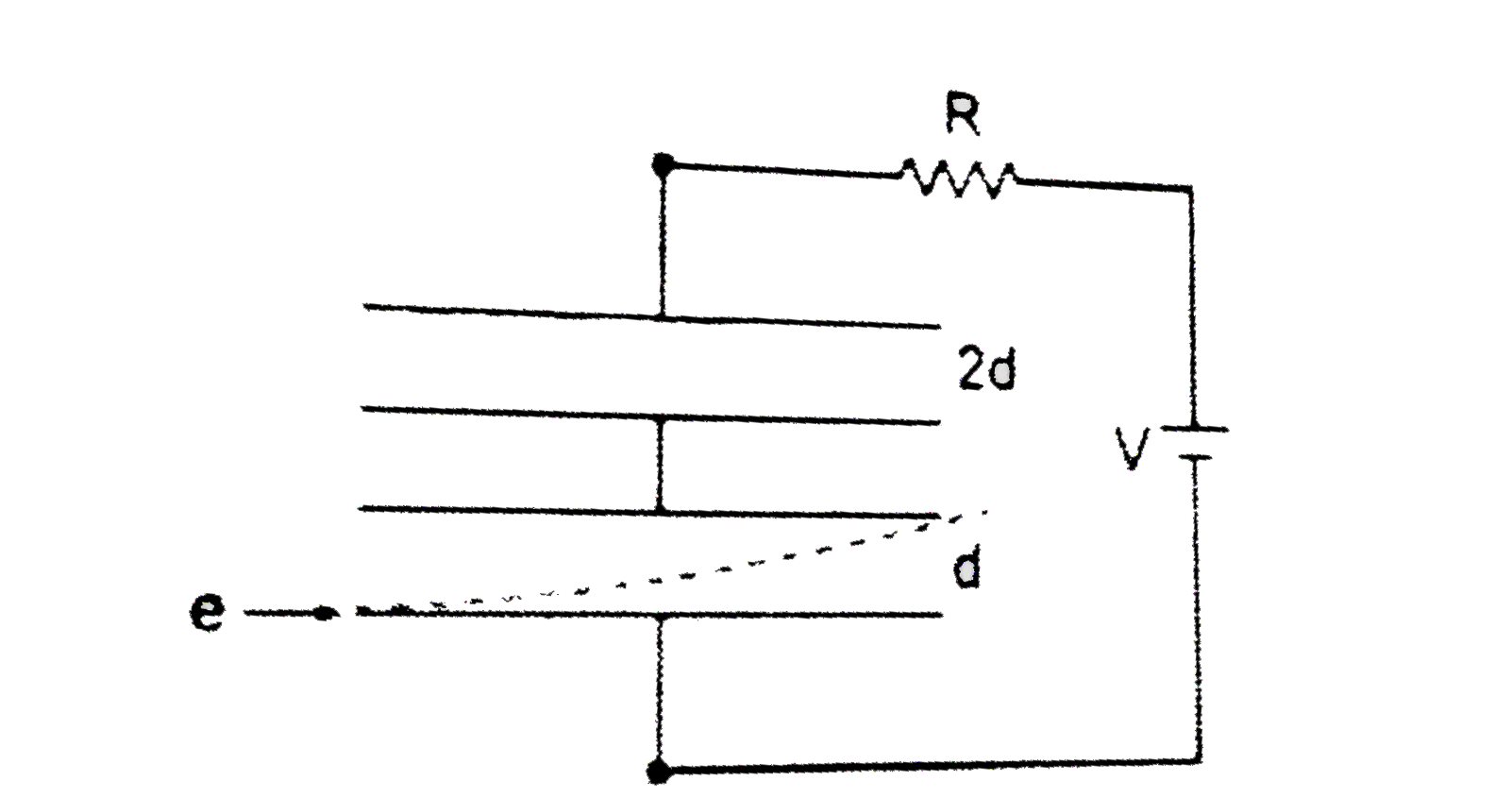 View Solution
View SolutionAn electron is projected from a distance d and with initial velocity u parallel to a uniformly charged flat conducting palte as shown. It strikes the plate after travelling a distance l along the direction of projection. The surface charge density of the conducting plate is equal to
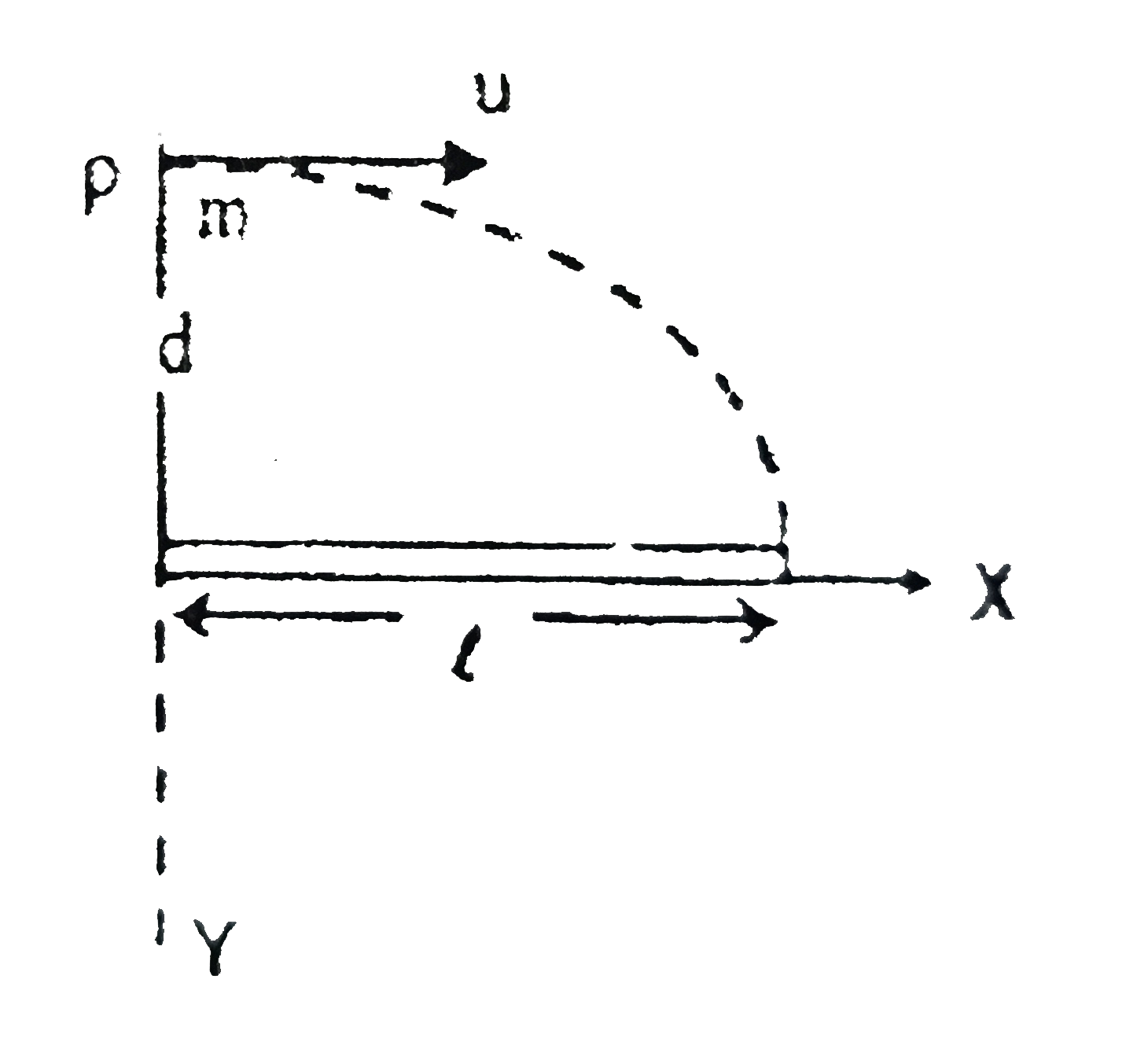 View Solution
View Solution

