If the range of the function y=x−1x+1 on the interval 0≤x≤4 be [a,b] then the value of 5b−2a=
To find the value of 5b−2a for the function y=x−1x+1 on the interval 0≤x≤4, we will follow these steps:
Step 1: Analyze the function
The function given is:
y=x−1x+1
We need to find the range of this function for x in the interval (0,4).
Step 2: Determine the endpoints
First, we will evaluate the function at the endpoints of the interval:
- For x=0:
y(0)=0−10+1=−11=−1
- For x=4:
y(4)=4−14+1=35
Step 3: Find critical points
Next, we find the derivative of the function to identify any critical points within the interval:
y=x−1x+1
Using the quotient rule, the derivative y′ is:
y′=(x+1)(1)−(x−1)(1)(x+1)2=(x+1)−(x−1)(x+1)2=2(x+1)2
Since y′>0 for all x≥0, the function is increasing on the interval (0,4).
Step 4: Determine the range
Since the function is increasing, the minimum value occurs at x=0 and the maximum value occurs at x=4. Therefore, the range of y on the interval (0,4) is:
(−1,35)
Thus, we have:
- a=−1
- b=35
Step 5: Calculate 5b−2a
Now we can calculate 5b−2a:
5b−2a=5(35)−2(−1)=3+2=5
Final Answer
The value of 5b−2a is:
5
The function given is:
y=x−1x+1
We need to find the range of this function for x in the interval (0,4).
First, we will evaluate the function at the endpoints of the interval:
- For x=0:
y(0)=0−10+1=−11=−1
- For x=4:
y(4)=4−14+1=35
Next, we find the derivative of the function to identify any critical points within the interval:
y=x−1x+1
Using the quotient rule, the derivative y′ is:
y′=(x+1)(1)−(x−1)(1)(x+1)2=(x+1)−(x−1)(x+1)2=2(x+1)2
Since y′>0 for all x≥0, the function is increasing on the interval (0,4).
Since the function is increasing, the minimum value occurs at x=0 and the maximum value occurs at x=4. Therefore, the range of y on the interval (0,4) is:
(−1,35)
Thus, we have:
- a=−1
- b=35
Now we can calculate 5b−2a:
5b−2a=5(35)−2(−1)=3+2=5
The value of 5b−2a is:
5
Topper's Solved these Questions
Similar Questions
The range of the function sin−1(x2+2x),x>0 is
View Solution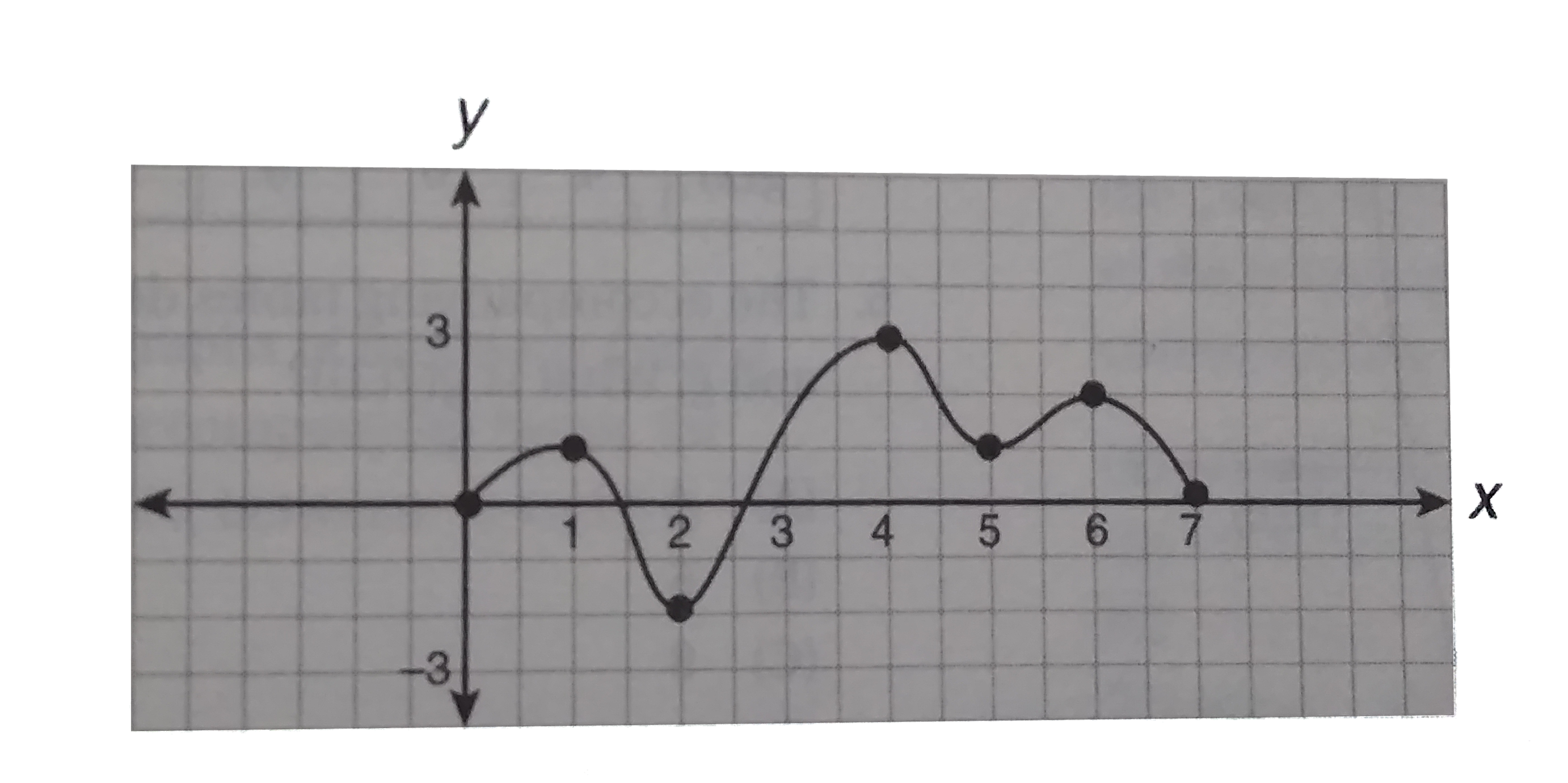
The graph above shows the function y=f(x) over the interval 0≤x≤7. What is the value of f(f(6))?
View SolutionIf the range of function f(x)=x+1k+x2 contains the interval
[-0,1] , then values of k can be equal to
View SolutionIf the range of the function f(x)=cot−1(x2x2+1) is (a, b), find the value of (ba+2).
View SolutionFind the range of the following functions.
y=x21+x2
View SolutionThe range of the function f(x)=x2ln(x) for x∈[1,e] is [a,b], where a+b is equal to
View SolutionIf the largest interval of x in which the function f(x)=x3−3x+1 is decreasing is (a, b), then the value of a+2b is equal to
View SolutionThe function f(x)=2x2−1x4,x>0decreases in the interval
View SolutionThe range of f(x)=(x+1)(x+2)(x+3)(x+4)+5 for x∈[−6,6] If the range of the function is [a,b] where a,b,∈N then find the value of(a+b).
View SolutionThe function y=ax+bx−1(x−4) has turning point at P(2,-1) Then find the values of a and b.
View Solution