Figure shows two coherent sources S1 and S2 vibrating in same phase. AB in an irregular wire lying at a far distance from the sources S1 and S2.Let λd=10−3∠BOA=0.12∘. How many bright spots will be seen on the wire, including points A and B?

NA
Topper's Solved these Questions
Similar Questions
Figure shows two coherent sources S1−S2 vibrating in same phase. AB is an irregular wire lying at a far distance from the sources S1 and S2. Let λd=10−3m,∠BOA=0.12∘. How many bright spots will be seen on the wire, including points A and B

View SolutionTwo coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View Solution
Knowledge Check
In the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
A(n+12)λBnλC(n−12)λDλ2
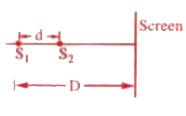
Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent sources S1 and S2 produce interference fringes. If a thin mica plate is introduced in the path of light from S1 then the central maximum
View SolutionTwo identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between the sources is 2λ. The smallest distance from S2 on a line passing through S2 and perpendicular to s1s2 where a minimum of intensity occurs is
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View SolutionThe coherent point sources S1 and S2 vibrating in same phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passingh through S2 and perpendicular to the line S1S2. What is the smallest distance from S2 where a minimum of intensity occurs due to interference of waves from the two sources?
View Solution
