Two particles are intially at a separation of d to each other. They move with constant velocirties with 5m/s and 3m/s respectively in horizontal plane. Their velocities makes an angle 60∘ with each other. If after 2 seconds, they collide. Then value of d is:
2√19m
8.7m
2m
32m
The correct Answer is:A
To solve the problem step by step, we will follow the given information and apply the concepts of relative velocity and displacement.
Step 1: Understand the Problem
We have two particles A and B moving with constant velocities of 5 m/s and 3 m/s, respectively, at an angle of 60° to each other. They collide after 2 seconds. We need to find the initial separation distance d between them.
Step 2: Determine the Velocities
Let:
- VA=5m/s (velocity of particle A)
- VB=3m/s (velocity of particle B)
- The angle between their velocities θ=60∘
Step 3: Calculate the Relative Velocity
The relative velocity VAB of particle A with respect to particle B can be calculated using the formula:
VAB=√V2A+V2B−2VAVBcos(θ)
Substituting the values:
VAB=√(5)2+(3)2−2⋅5⋅3⋅cos(60∘)
Since cos(60∘)=12:
VAB=√25+9−2⋅5⋅3⋅12
=√25+9−15
=√19m/s
Step 4: Calculate the Displacement Before Collision
The displacement SAB between the two particles before they collide can be calculated using the formula:
SAB=VAB×t
where t=2s.
Substituting the values:
SAB=√19×2
=2√19meters
Step 5: Calculate the Numerical Value
Now, we calculate 2√19:
√19≈4.3589(approximately)
Thus,
SAB≈2×4.3589≈8.7178meters
Step 6: Conclusion
The initial separation distance d between the two particles is approximately:
d≈8.7meters
Final Answer
The value of d is approximately 8.7 meters.
---
We have two particles A and B moving with constant velocities of 5 m/s and 3 m/s, respectively, at an angle of 60° to each other. They collide after 2 seconds. We need to find the initial separation distance d between them.
Let:
- VA=5m/s (velocity of particle A)
- VB=3m/s (velocity of particle B)
- The angle between their velocities θ=60∘
The relative velocity VAB of particle A with respect to particle B can be calculated using the formula:
VAB=√V2A+V2B−2VAVBcos(θ)
VAB=√(5)2+(3)2−2⋅5⋅3⋅cos(60∘)
VAB=√25+9−2⋅5⋅3⋅12
=√25+9−15
=√19m/s
The displacement SAB between the two particles before they collide can be calculated using the formula:
SAB=VAB×t
where t=2s.
SAB=√19×2
=2√19meters
Now, we calculate 2√19:
√19≈4.3589(approximately)
Thus,
SAB≈2×4.3589≈8.7178meters
The initial separation distance d between the two particles is approximately:
d≈8.7meters
The value of d is approximately 8.7 meters.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
Two identical balls are approaching towards each other on a straight line with velocity 2m/s and 4m/s, respectiely. Find the final velocities after elastic collision between them.

View SolutionTwo particles one of mass m and the other of mass 2 m are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s respectively . They collide in air and stick to each other . The distance from A , where the combined mass finally land is
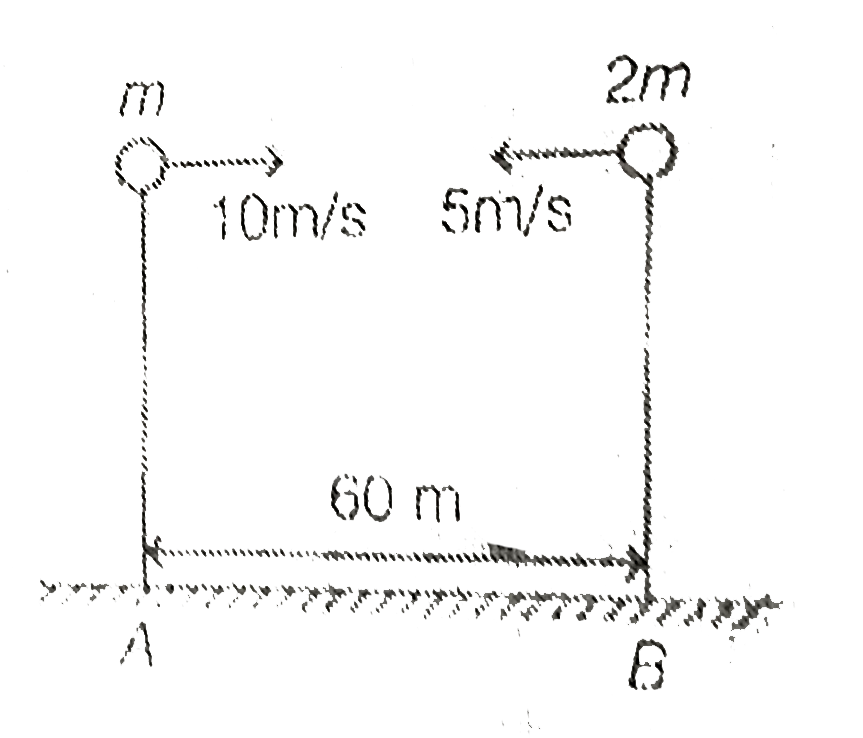
View Solution
Knowledge Check
Two identical balls A and B moving with velocities + 0.5 m/s and −0.3.m/s respectively collide head-on elastically. The velocities of the ball A and B after collision will be respectively
A+0.5m/sand+0.3m/sB−0.3m/sand+0.5m/sC + 0.3 m//s and + 0.5 m//sD−0.5m/sand+0.3m/s
Two particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively. They collide in air and stick to each other. The distance of the combined mass from point A is
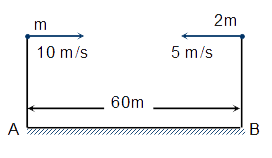
View SolutionTwo balls of masses m each are moving at right angle to each other with velocities 6 m/s and 8 m/s respectively. If collision between them is perfectly inelastic, the velocity of combined mass is
View SolutionTwo equal masses m1 and m2 moving along the same straight line with velocites +3m/s and −5m/s respectively collide elastically. Their velocities after the collision will be respectively.
View SolutionTwo equal masses m1 and m2 moving along the same straight line with velocites +3m/s and −5m/s respectively collide elastically. Their velocities after the collision will be respectively.
View SolutionTwo perfectly elastic particles A and B of equal masses travelling along a line joining them with velocities 15m/s and 10m/s respectively collide. Their velocities after the elastic collision will be (in m/s) respectively
View SolutionTwo perfectly elastic particles A and B of equal masses travelling along a line joining them with velocities 15m/s and 10m/s respectively collide. Their velocities after the elastic collision will be (in m/s) respectively
View SolutionTwo identiacal balls A and B having velocities of 0.5 m/s and 0.3 m/s respectively collide elastically in one dimension. The velocities of B and A after the collision respectively will be
View Solution
