The cubical container ABCDEFGH which is completely filled with an ideal (nonviscous and incompressible) fluid, moves in a gravity free space with a acceleration of a=a0(ˆi−ˆj+ˆk) where a0 is a positive constant. Then the minimum pressure at the point will be
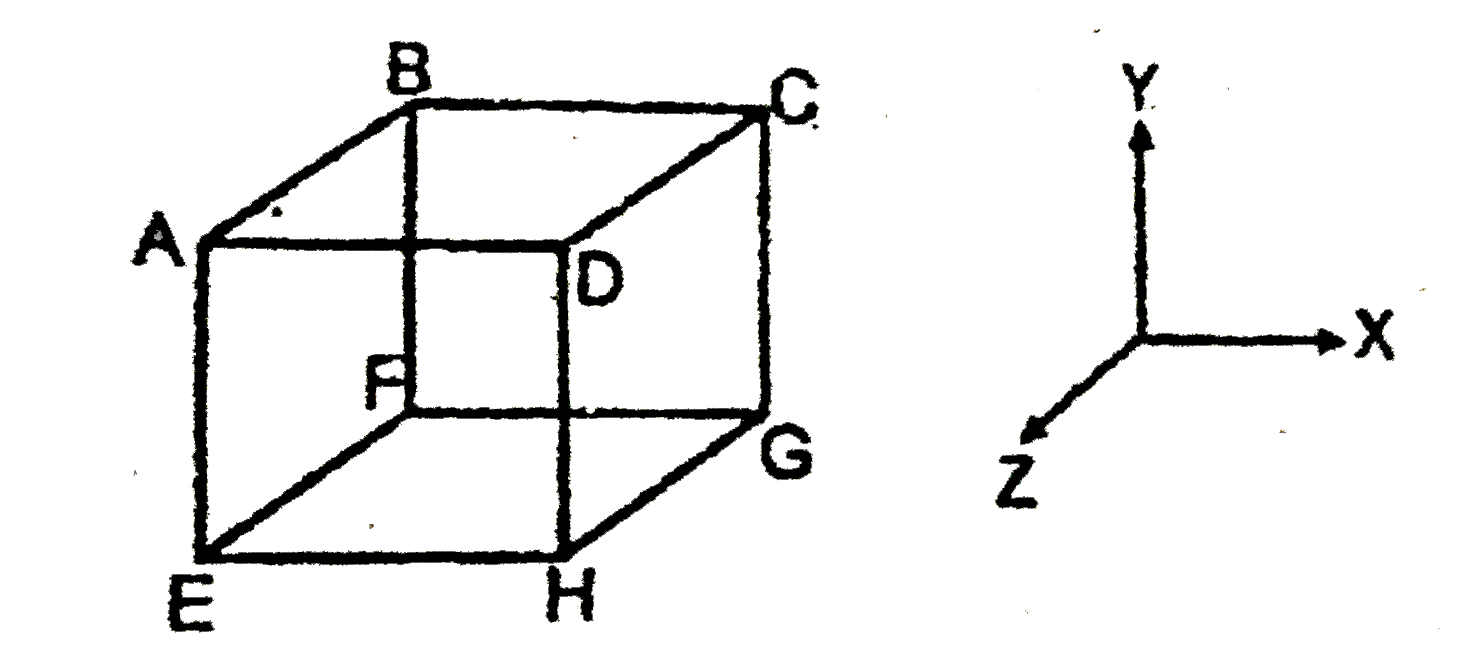
B
C
E
F
The correct Answer is:A
(i) a=a0(ˆi−ov(j)+∧k)
As there is no gravity. The pressure difference will be only due to the acceleration. At point B the preudo force is maximum hence pressure is maximum.
(ii) At point H the preudo force is minimum hence pressure is minimum
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - II Section (B)7videos
FLUID MECHANICS
- BOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - II Section (C)5videos
FLUID MECHANICS
- BOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - I Section (C)3videos
FLUID MECHANICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise52videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - FULL TEST 1EXERCISE - Exercise30videos
FULL TEST 1
Similar Questions
A positively charged particle is moving along the positive x-axis in a unifom electric field→E=E0ˆj and magnetic field →B=B0ˆk (where E0 and B0 are positive constants), then
View SolutionOne mole of an ideal gas undergoes a process in which T=T0+aV3, where T0 and a are positive constants and V is molar volume. The volume for which pressure with be minimum is
View SolutionOne mole of an ideal gas undergoes a process in which T=T0+aV3, where T0 and a are positive constants and V is molar volume. The volume for which pressure with be minimum is
View SolutionA particle of charge q>0 is moving at speed v in the +z direction through a region of uniform magnetic field. The magnetic force on the particle →F=F0(3ˆi+4ˆj), where F0 is a positive constant.
(a) Determine the components Bx,By and Bz or at least as many of the three components as is possible from the information given.
(b) If it is given in addition that the magnetic field has magnitude 6F0qv , determine the magnitude of Bz.View SolutionA paarticle starts from origin at t=0 with a velocity 5.0ˆim/s and moves in x-y plane under action of a force which produces a constant acceleration of (3.0ˆi+2.0j)m/s2.
(a) What is the y-cordinate of the particle at the instant its x-coordinate is 84 m ? (b) What is the speed of the particle at this time?View SolutionA particle initially (i.e., at t = 0) moving with a velocity u is subjected to a retarding force, as a result of which it decelerates a=−k√v at a rate where v is the instantaneous velocity and k is a positive constant. The time T taken by the particle to come to rest is given by :
View SolutionA U - shaped conducting frame is fixed in space. A conducting rod CD lies at rest on the smooth frame as shown. The frame is in a uniform magnetic field B0 which is perpendicular to be plane of the frame . At the time t = 0 , the magnitude of the magnetic field being to change with time t as, B=B01+kt , where k is a positive constant . For no current to be ever induced in the frame the speed with which rod should be pulled starting from time t = 0 is (the rod CD should be moved such that its velocity must lie in the plane of frame and perpendicular to rod (CD)
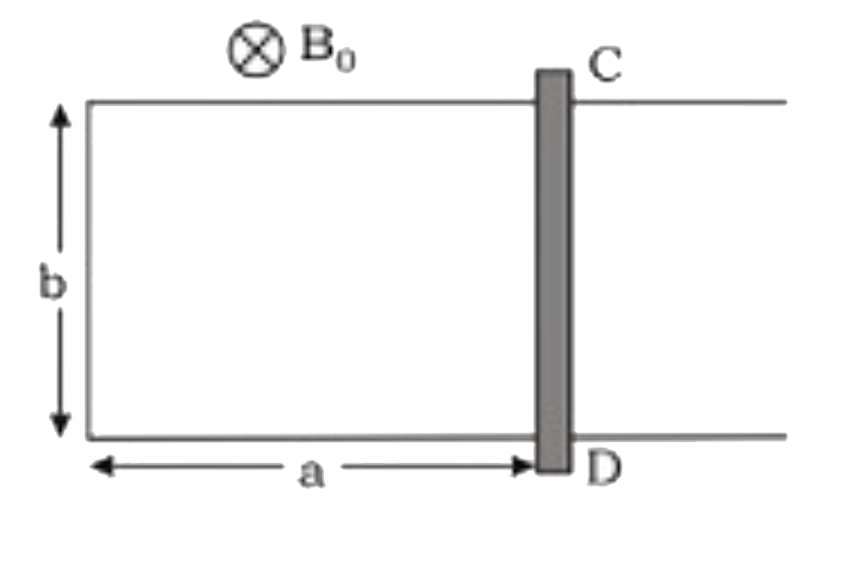 View Solution
View SolutionA magnetic field →B=B0ˆj , exists in the region a<x<2a , and →B=−B0ˆj , in the region 2a<x<3a, where B0 is a positive constant . A positive point charge moving with a velocity →v=v0ˆi , where v0 is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like
 View Solution
View SolutionA circle is the locus of a point in a plane such that its distance from a fixed point in the plane is constant. Anologously, a sphere is the locus of a point in space such that its distance from a fixed point in space in constant. The fixed point is called the centre and the constant distance is called the radius of the circle/sphere. In anology with the equation of the circle |z−c|=a, the equation of a sphere of radius a is |r−c|=a, where c is the position vector of the centre and r is the position vector of any point on the surface of the sphere. In Cartesian system, the equation of the sphere, with centre at (−g,−f,−h) is x2+y2+z2+2gx+2fy+2hz+c=0 and its radius is √f2+g2+h2−c. Q. Equation of the sphere having centre at (3,6,−4) and touching the plane r⋅(2ˆi−2ˆj−ˆk)=10 is (x−3)2+(y−6)2+(z+4)2=k2, where k is equal to
View SolutionA ball of mass M/2 filled with a gas ( whose mass is M/2) is kept on a frictionless table . A bullet of mass m=M/4 and velocity v0ˆi penetrates the ball , and rests inside at t=0. Assume that the amount of gas emitted during the collision can be neglected. The compressed gas is emitted at a contant velocity v0/2 relative to the ball and at an even rate k ( k is a positive constant ) .
(a) What is the velocity of the ball after the collision with the bullet ?
(b) Find the velocity of the ball v(t) as a function of time. Assume that the emission of gas starts at t=0. What is the final velocity of the ball ?
 View Solution
View Solution

