A thin disc of radius R, just touching the liquid surface forms one arm of a balance. The palte is balanced by some weight on the other side of the balance. How much extra weight should be added on the other side, so that the disc can just come cut of water ? 
Surface tension force on the disc is (T)(2πR)
For balance (T)(2πR)=(Δm)g⇒Δm=(T)(2πR)g
Topper's Solved these Questions
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - I
10 Videos
- SURFACE TENSIONBOOK - RESONANCE ENGLISHCHAPTER - SURFACE TENSIONEXERCISE - Exercise- 1 PART - II
16 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
- UNITS, DIMENSION & MEASUREMENTBOOK - RESONANCE ENGLISHCHAPTER - UNITS, DIMENSION & MEASUREMENTEXERCISE - Exercise
27 Videos
Similar Questions
In the previous question, in place of disc a ring is used whose inner radius is R1 and outer radius is R2 Now how much extra weight should be added on the other side, so that the ring can just come out of water ?
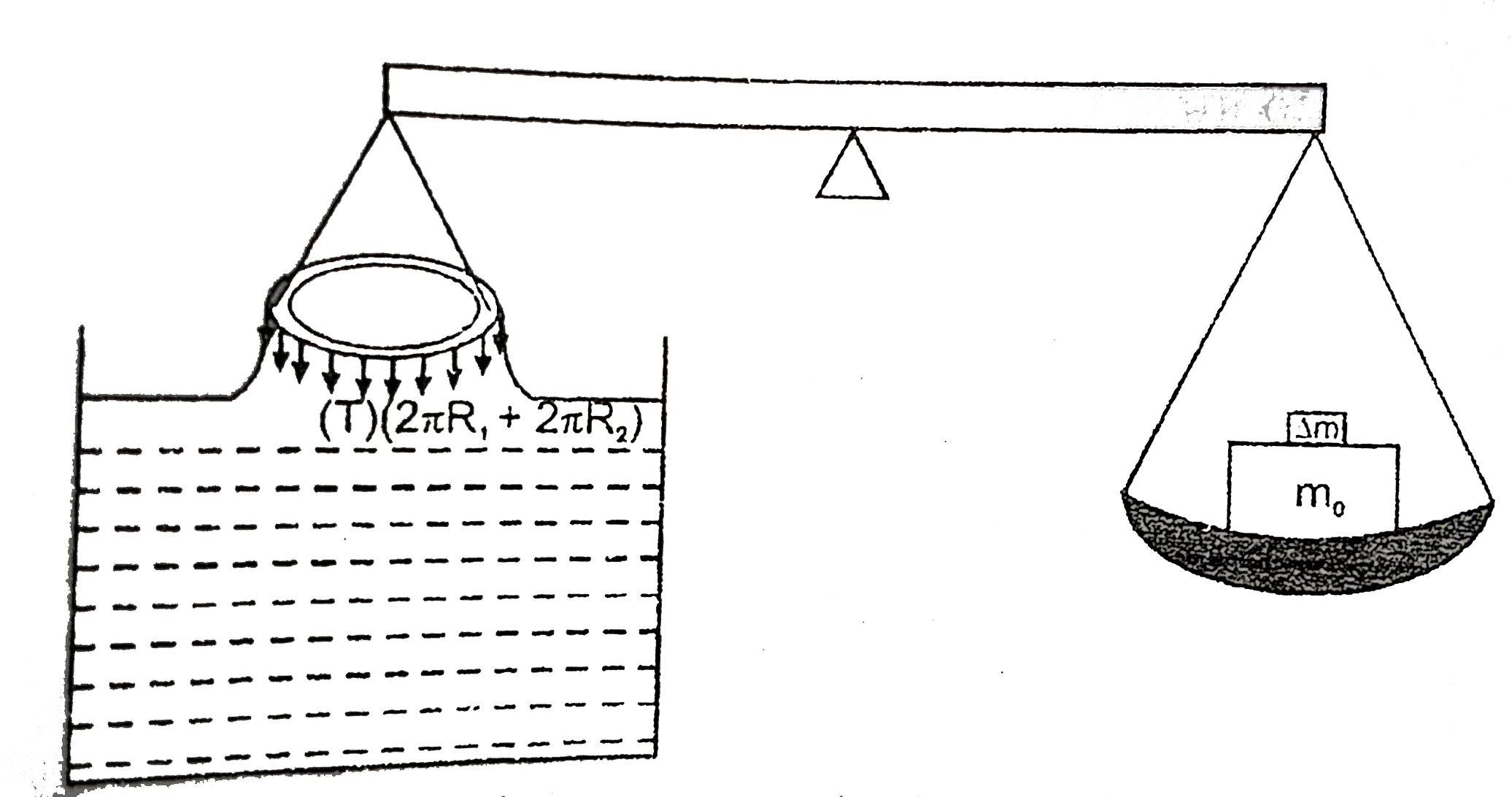
View SolutionIn the previous question, in place of disc a ring is used whose inner radius is R1 and outer radius is R2 Now how much extra weight should be added on the other side, so that the ring can just come out of water ?

View Solution
Knowledge Check
A solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?
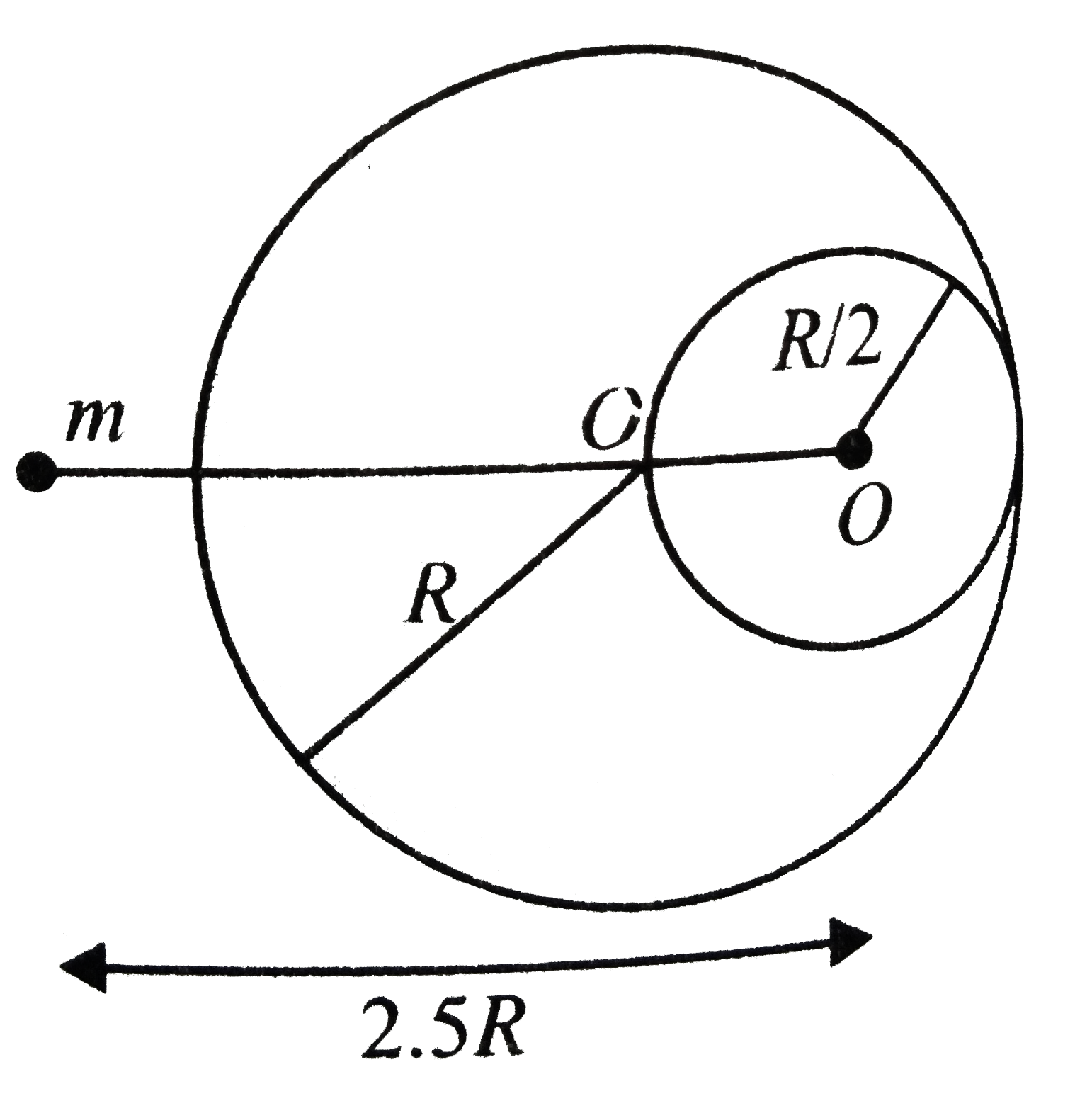 AGMmR2BGMm2R2CGMm8R2D23100GMmR2
AGMmR2BGMm2R2CGMm8R2D23100GMmR2A thin metal ring of internal radius 8 cm and external radius 9 cm is supported horizontally from the pan of a balance so that it comes in contact with water in a glass vessel. If is found that an extrea weight of 7.48g is required to pull the ring out of water. The surface tension of water is (g=10m/s2)
A80×10−3N/mB25×10−3N/mC45×10−3N/mD70×10−3N/m
Two transparent slabs having equal thickness but different refractive indices μ1andμ2, are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits ?
View SolutionTwo transparent slabs having equal thickness but different refractive indices μ1andμ2, are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits ?
View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?

View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?

View SolutionA thin metal ring of internal radius 8 cm and external radius 9 cm is supported horizontally from the pan of a balance so that it comes in contact with water in a glass vessel. If is found that an extrea weight of 7.48g is required to pull the ring out of water. The surface tension of water is (g=10m/s2)
View SolutionA circular ring of small thickness and of inner and outer diameters 3.8 cm and 4.2 cm respectively , suspended on one side of a common balance is exactly balanced by keeping sufficient mass in the pan on other side .At this instant the lower surface of ring is just resting on the surface of a liquid . Now if the ring is puled up gently , such that it does not loose its contact with the liquid , find how much mass should be changed in other pan , again to keep the balance in balanced position ? (Assume angle of contact is zero and surface tension of liquid is (1/π) N/m)
View Solution
