When a tensile or compressive load 'P' is applied to rod or cable, its length changes. The change length x which, for an elastic material is proportional to the force Hook' law).
Pαx or P=kx
The above equation is similar to the equation of spring. For a rod of length L, area A and young modulue Y. the extension xcan be expressed as.
x=PLAY or P=AYx, hence K=AYL
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called strain energy & equal to 12Px. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by energy conservation.
In above problem if mass of 10kg falls on the massless collar attached to rod from the height of 99cm then maximum extension in the rod is equal (rod of length 4m, area 4cm2 and young modules 2×1010N/m2 g=10m/sec2)-
9.9cm
10cm
0.99cm
1cm
The correct Answer is:D
To solve the problem of maximum extension in a rod when a mass falls on it, we can follow these steps:
Step 1: Identify the Given Values
- Mass of the object (m) = 10 kg
- Height from which the mass falls (h) = 99 cm = 0.99 m
- Length of the rod (L) = 4 m
- Cross-sectional area of the rod (A) = 4 cm² = 4 × 10⁻⁴ m²
- Young's modulus (Y) = 2 × 10¹⁰ N/m²
- Acceleration due to gravity (g) = 10 m/s²
Step 2: Calculate the Spring Constant (K)
Using the formula for the spring constant:
K=AYL
Substituting the values:
A=4×10−4m2
Y=2×1010N/m2
L=4m
Now substituting these into the formula:
K=(4×10−4)×(2×1010)4
K=8×1064
K=2×106N/m
Step 3: Calculate the Potential Energy (PE) of the Falling Mass
The potential energy when the mass is at height h is given by:
PE=mgh
Substituting the values:
PE=10×10×0.99
PE=99J
Step 4: Use Energy Conservation to Find Maximum Extension
At maximum extension, all potential energy is converted into strain energy stored in the rod:
PE=12Kx2max
Setting the two energies equal:
99=12(2×106)x2max
99=106x2max
Step 5: Solve for Maximum Extension xmax
Rearranging the equation:
x2max=99106
xmax=√99106
xmax=√0.000099
xmax=0.00995m
Converting to centimeters:
xmax≈1cm
Final Answer
The maximum extension in the rod is approximately 1 cm.
---
- Mass of the object (m) = 10 kg
- Height from which the mass falls (h) = 99 cm = 0.99 m
- Length of the rod (L) = 4 m
- Cross-sectional area of the rod (A) = 4 cm² = 4 × 10⁻⁴ m²
- Young's modulus (Y) = 2 × 10¹⁰ N/m²
- Acceleration due to gravity (g) = 10 m/s²
Using the formula for the spring constant:
K=AYL
A=4×10−4m2
Y=2×1010N/m2
L=4m
K=(4×10−4)×(2×1010)4
K=8×1064
K=2×106N/m
The potential energy when the mass is at height h is given by:
PE=mgh
Substituting the values:
PE=10×10×0.99
PE=99J
At maximum extension, all potential energy is converted into strain energy stored in the rod:
PE=12Kx2max
99=12(2×106)x2max
99=106x2max
Rearranging the equation:
x2max=99106
xmax=√99106
xmax=√0.000099
xmax=0.00995m
Converting to centimeters:
xmax≈1cm
The maximum extension in the rod is approximately 1 cm.
Topper's Solved these Questions
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 3 PART - I
7 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 3 PART - IV
9 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 2 PART - II
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 92 illustration
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
43 Videos
Similar Questions
When a tensile or compressive load 'P' is applied to rod or cable, its length changes. The change length x which, for an elastic material is proportional to the force Hook' law).
Pαx or P=kx
The above equation is similar to the equation of spring. For a rod of length L, area A and young modulue Y. the extension xcan be expressed as.
x=PLAY or P=AYx, hence K=AYL
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called stra energy & equal to 12Px. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by enerfy conservation.
If rod of length 4m, area 4cm2 amd young modules 2×1010N/m2 is attached with mass 200kg, then angular frequency of SHM (rad/sec.) of mass is equal to -
View SolutionWhen a tensile or compressive load 'P' is applied to rod or cable, its length changes. The change length x which, for an elastic material is proportional to the force Hook' law).
Pαx or P=kx
The above equation is similar to the equation of spring. For a rod of length L, area A and young modulue Y. the extension xcan be expressed as.
x=PLAY or P=AYx, hence K=AYL
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called stra energy & equal to 12Px. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by enerfy conservation.
It two rods of same length (4m) and cross section areas 2cm2 and 4cm2 with same young modulus 2×1010N/m2 are attached one after the other with mass 600kg then angular frequency is-
View SolutionWhen does an elastic metal rod change its length?
View SolutionA simple pendulum of length L has a period T. If length is changed by ΔL, the change in period ΔT is proportional to
View SolutionA rod of length L kept on a smooth horizontal surface is pulled along its length by a force F. The area of cross-section is A and Young's modulus is Y. The extension in the rod is

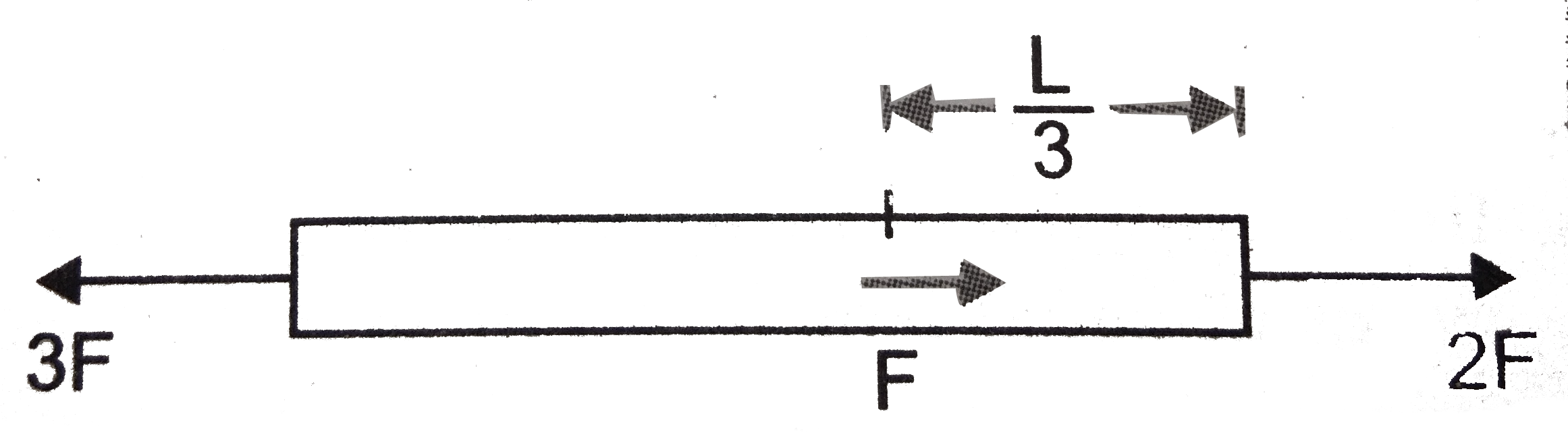
View SolutionA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
View SolutionThe length of a spring is α when a force of 4N is applied on it and the length is β when 5N is applied. Then the length of spring when 9N force is applied is-
View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View SolutionA rod is of length 3 m and its mass acting per unit length is directly proportional to distance x from its one end. The centre of gravity of the rod from that end will be at
View SolutionWhat is the percentage change in length of 1m iron rod it its temperature changes by 100∘C.α for iron is 2×10−5/∘C.
View Solution
