When a tensile or compressive load 'P' is applied to rod or cable, its length changes. The change length x which, for an elastic material is proportional to the force Hook' law).
Pαx or P=kx
The above equation is similar to the equation of spring. For a rod of length L, area A and young modulue Y. the extension xcan be expressed as.
x=PLAY or P=AYx, hence K=AYL
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called stra energy & equal to 12Px. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by enerfy conservation.
It two rods of same length (4m) and cross section areas 2cm2 and 4cm2 with same young modulus 2×1010N/m2 are attached one after the other with mass 600kg then angular frequency is-
10003
103
1003
10π3
The correct Answer is:C
To solve the problem step by step, we will follow the concepts of elasticity and the analogy of springs.
Step 1: Determine the spring constants for both rods.
We know that the spring constant K for a rod can be expressed as:
K=AYL
where:
- A = cross-sectional area
- Y = Young's modulus
- L = length of the rod
For Rod 1:
- Length L1=4m
- Area A1=2cm2=2×10−4m2
- Young's modulus Y=2×1010N/m2
Calculating K1:
K1=(2×10−4m2)(2×1010N/m2)4m=4×106N4=106N/m
For Rod 2:
- Length L2=4m
- Area A2=4cm2=4×10−4m2
Calculating K2:
K2=(4×10−4m2)(2×1010N/m2)4m=8×106N4=2×106N/m
Step 2: Find the effective spring constant for the two rods in series.
When two springs (or rods in this case) are connected in series, the effective spring constant Keffective is given by:
1Keffective=1K1+1K2
Substituting the values:
1Keffective=1106+12×106=22×106+12×106=32×106
Thus,
Keffective=2×1063N/m
Step 3: Calculate the angular frequency ω.
The angular frequency ω for a mass-spring system is given by:
ω=√Keffectivem
where m is the mass attached to the rods.
Given:
- Mass m=600kg
Substituting the values:
ω=
⎷2×1063600=√2×1061800=√200018=√10009=103rad/s
Final Answer:
The angular frequency is:
ω=1003rad/s
We know that the spring constant K for a rod can be expressed as:
K=AYL
where:
- A = cross-sectional area
- Y = Young's modulus
- L = length of the rod
- Length L1=4m
- Area A1=2cm2=2×10−4m2
- Young's modulus Y=2×1010N/m2
K1=(2×10−4m2)(2×1010N/m2)4m=4×106N4=106N/m
- Length L2=4m
- Area A2=4cm2=4×10−4m2
K2=(4×10−4m2)(2×1010N/m2)4m=8×106N4=2×106N/m
When two springs (or rods in this case) are connected in series, the effective spring constant Keffective is given by:
1Keffective=1K1+1K2
1Keffective=1106+12×106=22×106+12×106=32×106
Thus,
Keffective=2×1063N/m
The angular frequency ω for a mass-spring system is given by:
ω=√Keffectivem
where m is the mass attached to the rods.
- Mass m=600kg
ω=
⎷2×1063600=√2×1061800=√200018=√10009=103rad/s
The angular frequency is:
ω=1003rad/s
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 3 PART - I7videos
ELASTICITY AND VISCOCITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 3 PART - IV9videos
ELASTICITY AND VISCOCITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 2 PART - II6videos
ELASTICITY AND VISCOCITY
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 92 illustration2videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise43videos
ELECTROMAGNETIC INDUCTION
Similar Questions
When a tensile or compressive load 'P' is applied to rod or cable, its length changes. The change length x which, for an elastic material is proportional to the force Hook' law).
Pαx or P=kx
The above equation is similar to the equation of spring. For a rod of length L, area A and young modulue Y. the extension xcan be expressed as.
x=PLAY or P=AYx, hence K=AYL
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called stra energy & equal to 12Px. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by enerfy conservation.
If rod of length 4m, area 4cm2 amd young modules 2×1010N/m2 is attached with mass 200kg, then angular frequency of SHM (rad/sec.) of mass is equal to -View SolutionWhen a tensile or compressive load 'P' is applied to rod or cable, its length changes. The change length x which, for an elastic material is proportional to the force Hook' law).
Pαx or P=kx
The above equation is similar to the equation of spring. For a rod of length L, area A and young modulue Y. the extension xcan be expressed as.
x=PLAY or P=AYx, hence K=AYL
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called strain energy & equal to 12Px. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by energy conservation.
In above problem if mass of 10kg falls on the massless collar attached to rod from the height of 99cm then maximum extension in the rod is equal (rod of length 4m, area 4cm2 and young modules 2×1010N/m2 g=10m/sec2)-View Solution
Knowledge Check
- Question 1 - Select One
A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2L - Question 2 - Select One
The young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
AY2BYC2YD4Y
When does an elastic metal rod change its length?
View SolutionA simple pendulum of length L has a period T. If length is changed by ΔL, the change in period ΔT is proportional to
View SolutionA metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y,then the work done is proportional to
View SolutionA rod of length L kept on a smooth horizontal surface is pulled along its length by a force F. The area of cross-section is A and Young's modulus is Y. The extension in the rod is
 View Solution
View SolutionA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
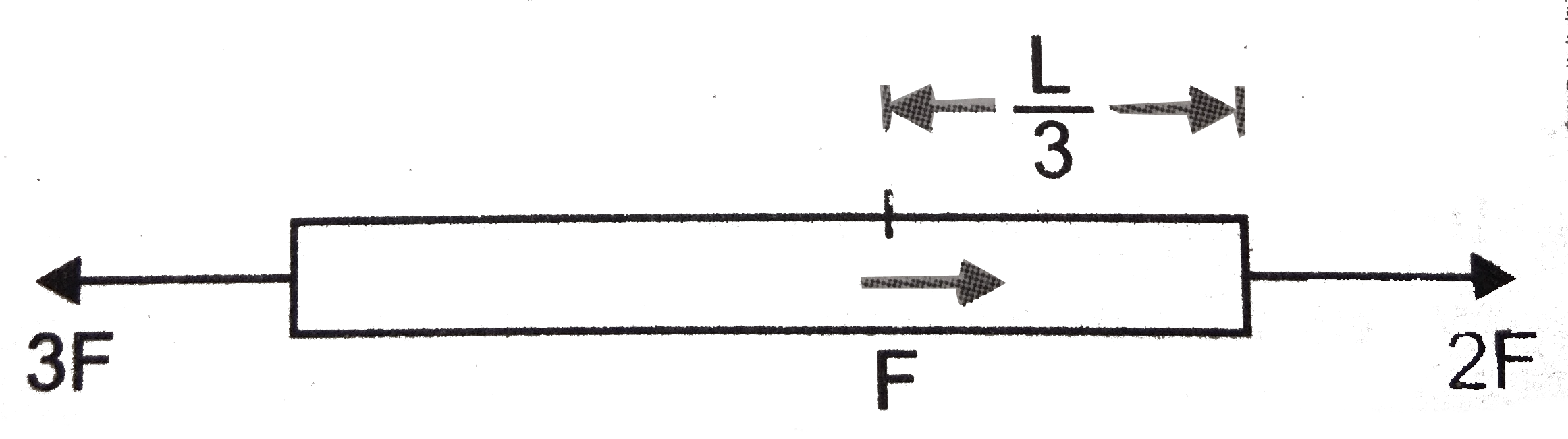 View Solution
View SolutionThe young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
View Solution

