An observer rides with a sound source of frequency f and moving with velocity v towards a large vertical wall. Considering the velocity of sound waves as c, find :
(i) The number of waves striking the surface of wall per second
(ii) The wavelength of the reflected wave
(iii) The frequency of reflected wave as observed by observer.
(iv) Beat frequency heard by the observer.
The correct Answer is:(i) f'=fcc−v
(ii) λ'=λ−(vf)=(cf)−(vf)=(c−vf)
f''=f(c+v)c−v
(iv) fbeat=f(2v)c−v
To solve the problem step by step, we will break down each part of the question:
Given:
- Frequency of sound source = f
- Velocity of observer (and sound source) = v
- Velocity of sound = c
(i) The number of waves striking the surface of the wall per second
1. Calculate the frequency of the sound waves as perceived by the wall:
The frequency f1 of the sound waves emitted by the source is given by:
f1=cc−vf
Here, c−v is the effective speed of sound relative to the wall since the observer is moving towards it.
2. Number of waves striking the wall per second:
The number of waves striking the wall per second is equal to the frequency f1:
N=f1=cc−vf
(ii) The wavelength of the reflected wave
1. Calculate the wavelength of the reflected wave:
The wavelength λ of the reflected wave can be found using the relationship:
λ=cf1
Substituting f1 from above:
λ=ccc−vf=(c−v)f
(iii) The frequency of the reflected wave as observed by the observer
1. Calculate the frequency of the reflected wave:
The frequency of the reflected wave f2 as perceived by the observer moving towards the wall is given by:
f2=c+vcf1
Substituting f1:
f2=c+vc⋅cc−vf=(c+v)(c−v)f
(iv) Beat frequency heard by the observer
1. Calculate the beat frequency:
The beat frequency fb is the difference between the frequency of the reflected wave and the original frequency:
fb=f2−f=(c+vc−vf)−f
Simplifying this:
fb=(c+vc−v−1)f=((c+v)−(c−v)c−v)f=2vc−vf
Summary of Results:
1. Number of waves striking the wall per second: N=cc−vf
2. Wavelength of the reflected wave: λ=(c−v)f
3. Frequency of the reflected wave: f2=(c+v)(c−v)f
4. Beat frequency heard by the observer: fb=2vc−vf
- Frequency of sound source = f
- Velocity of observer (and sound source) = v
- Velocity of sound = c
The frequency f1 of the sound waves emitted by the source is given by:
f1=cc−vf
Here, c−v is the effective speed of sound relative to the wall since the observer is moving towards it.
The number of waves striking the wall per second is equal to the frequency f1:
N=f1=cc−vf
The wavelength λ of the reflected wave can be found using the relationship:
λ=cf1
Substituting f1 from above:
λ=ccc−vf=(c−v)f
The frequency of the reflected wave f2 as perceived by the observer moving towards the wall is given by:
f2=c+vcf1
Substituting f1:
f2=c+vc⋅cc−vf=(c+v)(c−v)f
The beat frequency fb is the difference between the frequency of the reflected wave and the original frequency:
fb=f2−f=(c+vc−vf)−f
Simplifying this:
fb=(c+vc−v−1)f=((c+v)−(c−v)c−v)f=2vc−vf
1. Number of waves striking the wall per second: N=cc−vf
2. Wavelength of the reflected wave: λ=(c−v)f
3. Frequency of the reflected wave: f2=(c+v)(c−v)f
4. Beat frequency heard by the observer: fb=2vc−vf
Topper's Solved these Questions
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 1 PART - II
30 Videos
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - I
24 Videos
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Board Level Exercise
33 Videos
- SIMPLE HARMONIC MOTIONBOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise
28 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
Similar Questions
A person with vibrating tuning fork of frequency 338 Hz is moving towards a vertical wall with speed of 2ms−1 Velocity of sound in air is 340ms−1 The number of beats heard per second is
View SolutionA sound wave of frequency f travels horizontally to the right . It is teflected from a larger vertical plane surface moving to left with a speed v. the speed of sound in medium is c
(a) The number of waves striking the surface per second is f(c+υ)c
(b) The wavelength of reflected wave is c(c−υ)f(c+υ)
(c) The frequency of the reflected wave is f((c+υ))(c+υ)
(d) The number of beats heard by a stationary listener to the left of the reflecting surface is υfc−υ
View Solution
Knowledge Check
The frequency of a sound wave is n and its velocity is v. If the frequency is increased to 4n, the velocity of wave will be
AvB2 vC4 vDv/4
Speed of sound wave is v. If a reflector moves towards a stationary source emitting waves of frequency f with speed u, the wavelength of reflected waves will be
View SolutionA source of sound with frequency 256Hz is moving with a velocity V towards a wall and an observer is stationary between the source and the wall. When the observer is between the source and the wall he will hear beats.
View SolutionA source of sound with frequency 256Hz is moving with a velocity V towards a wall and an observer is stationary between the source and the wall. When the observer is between the source and the wall will he hear beats?
View SolutionA source of sound which emitting a sound of frequency 600 Hz is moving towards a wall with a velocity 30 m/s. Three observes A, B, C moving with velocity 20 m/s, A away from the wall and B towards the wall and Inside the source, Velocity of sound in air is 330 m/s.

Find the frequency of reflected sound observed by observer B
View SolutionWhen both the listener and source are moving towards each other, then which of the following is true regarding frequency and wavelength of wave observed by the observer?
View SolutionIf sound wave of frequency 500Hz and wavelength 0.66m is travelling in a medium. Calculate the velocity of the wave in the medium.
View SolutionA source of sound which emitting a sound of frequency 600 Hz is moving towards a wall with a velocity 30 m/s. Three observes A, B, C moving with velocity 20 m/s, A away from the wall and B towards the wall and Inside the source, Velocity of sound in air is 330 m/s.
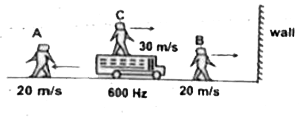
Find the frequency of direct sound observed by observer A
View Solution
