When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value
The correct Answer is:D
To solve the question regarding the sound produced when we clap our hands, we need to analyze the options provided and understand the nature of sound waves generated during the clap.
1. Understanding Sound Waves: When we clap our hands, we create a disturbance in the air, which generates sound waves. These sound waves can be described mathematically.
2. Analyzing the Options:
- Option 1: P=P0sin(kx−ωt) - This represents a simple harmonic wave traveling in one direction.
- Option 2: P=P0sin(kx)cos(ωt) - This represents a wave that can be seen as a product of two functions, indicating a stationary wave.
- Option 3: P=P0cos(kx−ωt) - This is another form of a simple harmonic wave.
- Option 4: P=∑P0sin(knx−ωnt) - This represents the summation of multiple waves, indicating the presence of a group of waves.
3. Identifying the Correct Option:
- When we clap our hands, multiple sound waves of different frequencies and wavelengths are produced due to the rapid motion and the complex nature of the clap. Therefore, the sound produced is not just a single wave but a combination of many waves.
- Hence, the best description of the sound produced when we clap our hands is given by Option 4, which accounts for the summation of multiple waves.
Conclusion:
The correct answer is Option 4: P=∑P0sin(knx−ωnt).
- Option 1: P=P0sin(kx−ωt) - This represents a simple harmonic wave traveling in one direction.
- Option 2: P=P0sin(kx)cos(ωt) - This represents a wave that can be seen as a product of two functions, indicating a stationary wave.
- Option 3: P=P0cos(kx−ωt) - This is another form of a simple harmonic wave.
- Option 4: P=∑P0sin(knx−ωnt) - This represents the summation of multiple waves, indicating the presence of a group of waves.
- When we clap our hands, multiple sound waves of different frequencies and wavelengths are produced due to the rapid motion and the complex nature of the clap. Therefore, the sound produced is not just a single wave but a combination of many waves.
- Hence, the best description of the sound produced when we clap our hands is given by Option 4, which accounts for the summation of multiple waves.
The correct answer is Option 4: P=∑P0sin(knx−ωnt).
Topper's Solved these Questions
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - II
20 Videos
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - III
19 Videos
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 1 PART - II
30 Videos
- SIMPLE HARMONIC MOTIONBOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise
28 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
Similar Questions
Physical and chemical equilibrium can respond to a change in their pressure, temperature, and concentration of reactants and products. To describe the change in the equilibrium we have a principle named Le Chatelier principle. According to this principle, even if we make some changes in equilibrium, then also the system even re-establishes the equilibrium by undoing the effect.
In the reaction N2(g)+3H2(g)⇔2NH3(g). If we increase the pressure of the system, the equilibrium is
View SolutionPhysical and chemical equilibrium can respond to a change in their pressure, temperature, and concentration of reactants and products. To describe the change in the equilibrium we have a principle named Le Chatelier principle. According to this principle, even if we make some changes in equilibrium, then also the system even re-establishes the equilibrium by undoing the effect.
If we add SO2−4 ion to a saturated solution of Ag2SO4, it will result in a//an
View Solution
Knowledge Check
An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
A12π√MV0AγP0B12πAγP0V0MC12πV0MP0A2γD12π√A2γP0MV0
Physical and chemical equilibria can respond to a change in their pressure, temperature, and concentration of reactants and products. To describe the change in the equilibrium, we have a principle named Le Chatelier's principle. This we can define in terms of energy, as the free energy change in equilibrium is zero means the system is stable. So if we are doing some changes in equilibrium, then the system having a tendency to reestablish the equilibrium by undoing the effect we brought. Consider the following equilibrium.
Three sparingly soluble salts A2B,AB, and AB3 are given. If all the three having the same value of solubility products (Ksp), in the saturated solution, the correct order of their solubilites is
View SolutionA vessel at 1000K contains CO2(g) at 2 atm pressure. When graphite is added the following equilibrium is established.
CO2(g)+C(s)⇔2CO(g)
the toal pressure at equilibrium is 3 atm. The value of Kp is
View SolutionA reaction is spontaneous if free energy change ΔG for the reaction is negative . The question arises, how we can explain , the spontaneous reversible reaction. Taking the example of dissociation equilibrium N2O4⇔2NO2(g) the variation of free energy with the fraction of N2O4 dissociated under standard conditions is shown in the figure below.

When 1 mole of N2O4 changes into the equilibrium mixture the value of ΔG∘ is
View SolutionThe pressure wave, P=0.01sin[1000t−3x]Nm−2, corresponds to the sound produced by a vibrating blabe on a day when a atmospheric temperature si 0∘C. On some other day when temperature is T, the speed of sound produced by the same blade and at the same frequency is found to be 336ms−1. Approximate value of T is :
View SolutionA reaction is spontaneous if free energy change ΔG , for the reaction is negative . The question arises, how we can explain , the spontaneous of reversible reaction taking the example of dissociation equilibrium N2O4⇔2NO2(g) the variation of free energy with the fraction of N2O4 dissociated under standard conditions is shown in the figure below.
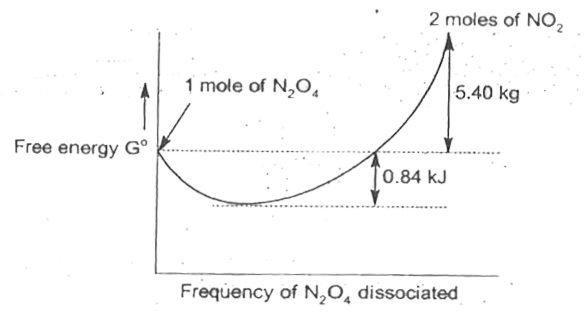
When 2 moles of NO2 change into equilibrium mixture the value of ΔG∘ is
View SolutionThe value of Kp for the reaction,
2SO2(g)+O2(g)⇔2SO3(g) is 5
what will be the partial pressure of O2 at equilibrium when equal moles of SO2andSO3 are present at equilibrium ?
View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View Solution
