Two plane parallel conducting plates 1.5×10−2m apart are held horizontal one above the other in air. The upper plate is maintained at a positive potential of1.5kV while the other plate is earthed. Calculate the number of electrons which must be attached to a small oil drop of mass 4.8×10−15kg between the plates of move the drop with constant speed. Neglect the density and viscosity of air.
The correct Answer is:3
To solve the problem, we need to calculate the number of electrons that must be attached to a small oil drop so that it moves with constant speed between two parallel conducting plates. Here are the steps to arrive at the solution:
Step 1: Identify the Forces Acting on the Oil Drop
The oil drop experiences two main forces:
1. The gravitational force acting downward, Fg=mg
2. The electric force acting upward, Fe=qE
Where:
- m is the mass of the oil drop
- g is the acceleration due to gravity (approximately 9.81m/s2)
- q is the charge on the oil drop (which is the product of the number of electrons n and the charge of an electron e)
- E is the electric field between the plates
Step 2: Calculate the Electric Field E
The electric field E between two parallel plates is given by the formula:
E=Vd
Where:
- V is the potential difference between the plates (in volts)
- d is the separation between the plates (in meters)
Given:
- V=1.5kV=1500V
- d=1.5×10−2m
Substituting the values:
E=1500V1.5×10−2m=100000V/m
Step 3: Set Up the Equation for Constant Speed
For the oil drop to move with constant speed, the net force acting on it must be zero. Thus, we can equate the gravitational force to the electric force:
mg=qE
Substituting q=ne (where e is the charge of an electron, e=1.6×10−19C):
mg=neE
Step 4: Solve for the Number of Electrons n
Rearranging the equation gives:
n=mgeE
Step 5: Substitute the Known Values
Given:
- m=4.8×10−15kg
- g=9.81m/s2
- e=1.6×10−19C
- E=100000V/m
Substituting these values into the equation:
n=(4.8×10−15kg)(9.81m/s2)(1.6×10−19C)(100000V/m)
Calculating the numerator:
mg=4.8×10−15×9.81=4.70688×10−14N
Calculating the denominator:
eE=(1.6×10−19)(100000)=1.6×10−14N
Now substituting back:
n=4.70688×10−141.6×10−14≈2.94≈3
Final Answer:
The number of electrons that must be attached to the oil drop is approximately n=3.
---
The oil drop experiences two main forces:
1. The gravitational force acting downward, Fg=mg
2. The electric force acting upward, Fe=qE
- m is the mass of the oil drop
- g is the acceleration due to gravity (approximately 9.81m/s2)
- q is the charge on the oil drop (which is the product of the number of electrons n and the charge of an electron e)
- E is the electric field between the plates
The electric field E between two parallel plates is given by the formula:
E=Vd
Where:
- V is the potential difference between the plates (in volts)
- d is the separation between the plates (in meters)
- V=1.5kV=1500V
- d=1.5×10−2m
E=1500V1.5×10−2m=100000V/m
For the oil drop to move with constant speed, the net force acting on it must be zero. Thus, we can equate the gravitational force to the electric force:
mg=qE
mg=neE
Rearranging the equation gives:
n=mgeE
Given:
- m=4.8×10−15kg
- g=9.81m/s2
- e=1.6×10−19C
- E=100000V/m
n=(4.8×10−15kg)(9.81m/s2)(1.6×10−19C)(100000V/m)
mg=4.8×10−15×9.81=4.70688×10−14N
eE=(1.6×10−19)(100000)=1.6×10−14N
n=4.70688×10−141.6×10−14≈2.94≈3
The number of electrons that must be attached to the oil drop is approximately n=3.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
Two parallel conducting plates of area A=2.5m2 each are placed 6 mm apart and are both earthed. A third plate, identical with the first two, is placed at a distance of 2 mm from one of the earthed plates and is given a charge of 1 C. The potential of the central plate is

View SolutionTwo metal plates of area 2×10−4m2 each, are kept in water and one plate is moved over the other with a certain velocity. The distance between the plates is 2×10−4m. If the horizontal force applied to move the plate is 10−3N, calculate the velocity of the plate. Given η of water is10−3 decapoise.
View Solution
Knowledge Check
Two large, thin plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 16×10−22Cm−2. The electric field between the plates is
A1.8×10−10NC−1B1.9×10−10NC−1C1.6×10−10NC−1D1.5×10−10NC−1
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0×10−22C/m2. What is E : between the plates?
View SolutionTwo large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0×10−22C/m2. What is E : between the plates?
View SolutionAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.
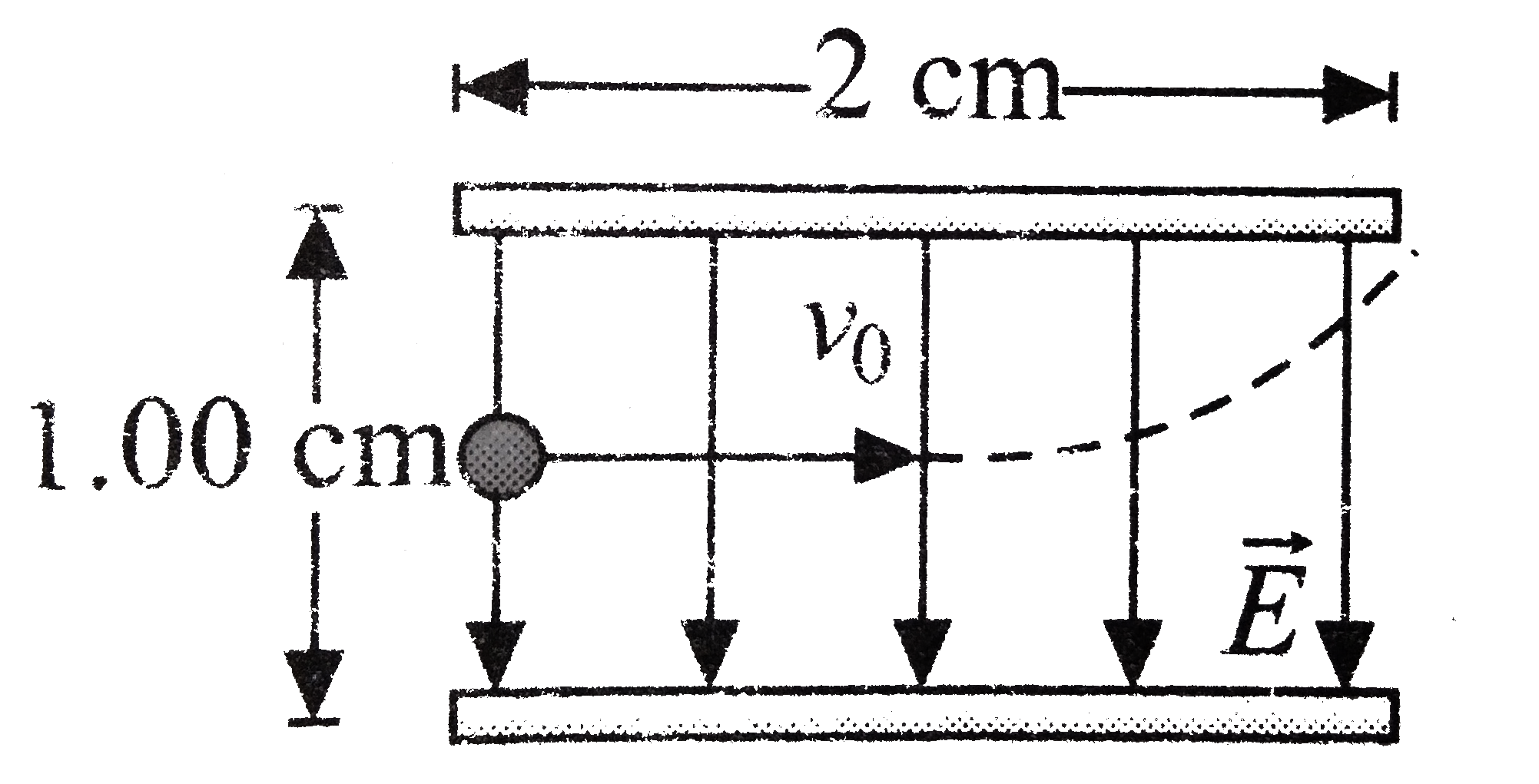
The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).
View SolutionAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.

The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).
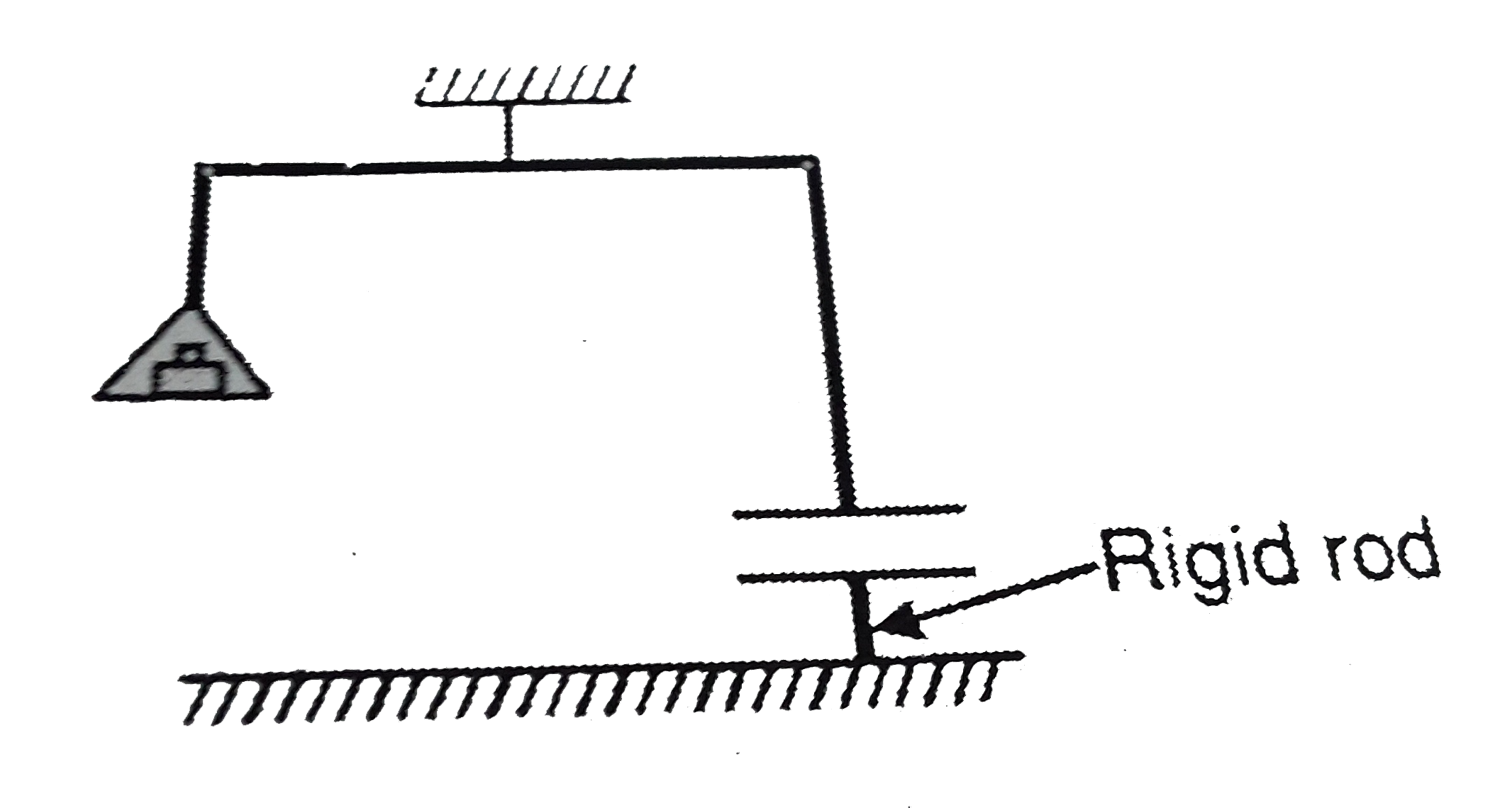
View SolutionThe lower plate of a parallel plate capacitor is supported on a rigid rod. The upper plate is suspended from one end of a balance. The two plates are joined together by a thin wire and subsequently disconnected. The balance is then counterpoised. Now a voltage V = 5000 volt is applied between the plates. The distance between the plates is d = 5 mm and the area of each plate is A =100cm2. Then find out the additional mass placed to maintain balance. [All the elements other than plates are massless and nonconducting]
View SolutionThe potential difference between two large parallel plates is varied as v = at, a is a positive constant and t is time. An electron starts from rest at t=0 from the plate which is at lower potential. If the distance between the plates is L, mass of electron m and charge on electron -e then find the velocity of the electron when it reaches the other plate.
View SolutionA capacitor is composed of three parallel conducting plates. All three plates are of the same area A. The first pair of plates are kept a distance d1 apart, and the space between them is filled with a medium of a dielectric K1 . The corresponding data of the second pair are d2 and K2, respectively. The middle plate is connected to the positive terminal of a constant voltage source V and the external plates are connected the other terminal of V.

(a) Find the capacitance of the system .
(b) What is the surface charge density on the middle plate ?
(c) Compute the energy density in the medium K1
View Solution
