Taking the open end of tube as position of pressure nodes will be .
None of these
To determine the positions of pressure nodes in an open tube, we can follow these steps:
1. Understanding the Concept of Pressure Nodes:
- In a tube that is open at one end, the open end is a pressure node (minimum pressure) and is typically taken as the reference point (y = 0).
- The closed end of the tube would be a pressure antinode (maximum pressure).
2. Identifying the Positions of Pressure Nodes:
- For an open tube, the positions of pressure nodes can be determined using the formula for nodes in a standing wave.
- The pressure nodes occur at specific intervals along the length of the tube.
3. Setting the Reference Point:
- We set the open end of the tube at y = 0. This means that the first pressure node will be at a distance of 1 cm from the open end (y = 1 cm).
4. Calculating Further Nodes:
- The next pressure node will be at y = -1 cm (below the open end).
- Continuing this pattern, we can find that the next pressure node occurs at y = 49 cm (assuming the total length of the tube allows for this position).
5. Finalizing the Positions:
- Thus, the positions of the pressure nodes are:
- y = -1 cm
- y = 1 cm
- y = 49 cm
6. Choosing the Correct Option:
- Based on the calculated positions of the pressure nodes, we can conclude that the correct option is A, which lists these positions.
Final Answer:
The positions of the pressure nodes are at y = -1 cm, y = 1 cm, and y = 49 cm. Therefore, the correct option is A.
---
- In a tube that is open at one end, the open end is a pressure node (minimum pressure) and is typically taken as the reference point (y = 0).
- The closed end of the tube would be a pressure antinode (maximum pressure).
- For an open tube, the positions of pressure nodes can be determined using the formula for nodes in a standing wave.
- The pressure nodes occur at specific intervals along the length of the tube.
- We set the open end of the tube at y = 0. This means that the first pressure node will be at a distance of 1 cm from the open end (y = 1 cm).
- The next pressure node will be at y = -1 cm (below the open end).
- Continuing this pattern, we can find that the next pressure node occurs at y = 49 cm (assuming the total length of the tube allows for this position).
- Thus, the positions of the pressure nodes are:
- y = -1 cm
- y = 1 cm
- y = 49 cm
- Based on the calculated positions of the pressure nodes, we can conclude that the correct option is A, which lists these positions.
The positions of the pressure nodes are at y = -1 cm, y = 1 cm, and y = 49 cm. Therefore, the correct option is A.
Topper's Solved these Questions
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Exercise
12 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Exercise -1 PART
1 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
Similar Questions
The water level in a vertical glass tube 1.0m long can be adjusted to any position in the tube . A tuning fork vibrating at 660HZ is held just over the open top end of the tube . At what positions of the water level wil they be in resonance? Speed of sound is 330m/s .
View SolutionA barometer tube reads 76 cm of Hg. If tube is : gradually inclined at an angle of 60∘ with vertical, keeping the open end in the mercury reservoir, the length of mercury column will be
View SolutionA barometer tube reads 76 cm of mercury. If the tube is gradually inclined keeping the open end immersed in the mercury reservoir, will the length of mercury column be 76 cm, more than 76 cm or less than 76 cm?
View SolutionA tuning fork of frequency n is held near the open end of tube, the tube is adjusted until resonance occurs. If the two shortest lengths to produce resonance are L1andL2 , then the speed of the sound is
View Solution_S01_057_Q01.png)
A liquid of density ρ is filled in a U-tube, whose one end is open & at the other end a bulb is fitted whose pressure is PA. Now this tube is moved horizontally with acceleration a as shown in the figure. during motion it is found that liquid in both column is at same level at equilibrium if atmospheric pressure is P0 then value of PA is
View SolutionAn open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. What will be length of the air column above mercury in the tube now? (atmospheric pressure =76 cm of Hg)
View SolutionAn open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. What will be length of the air column above mercury in the tube now? (atmospheric pressure =76 cm of Hg)
View SolutionIn a resonace tube experiment, the first resonance is obtained when the level of the water in the tube is at 20 cm from the open end. Resonace will also be obtained when the distance of the water level from the open end is
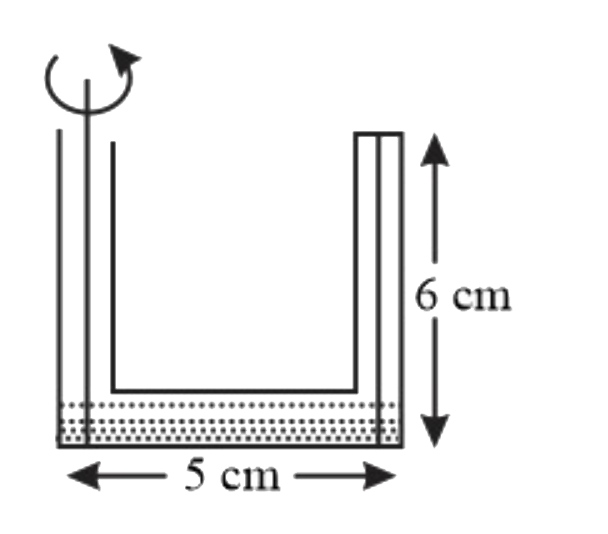
View SolutionLength of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
View SolutionIn an organ pipe ( may be closed or open of 99cm length standing wave is setup , whose equation is given by longitudinal displacement ξ=(0.1mm)cos(2π)0.8(y+1cm)cos2π(400)t
where y is measured from the top of the tube in metres and t in second. Here 1cm is th end correction.

Assume end correction approximately equals to (0.3)×(diameter of tube) , estimate the moles of air pressure inside the tube (Assume tube is at NTP , and at NTP,22.4litre contain 1mo≤)
View Solution
