If the unknown Resistancee calculated without using the end correction is R1 and with using end corrections is R2 then (assume same end corection) .
R1>R2 when balanced point is in first half
R1>R2 when balanced point is in first half
R1>R2 when balanced point is in first half
R1>R2 when balanced point is in first half
To solve the problem, we need to establish the relationship between the unknown resistances R1 and R2 calculated with and without end corrections, respectively.
1. Understand the Definitions:
- Let R1 be the resistance calculated without using the end correction.
- Let R2 be the resistance calculated with the end correction.
2. Formulate the Expressions:
- The formula for R1 (without end correction) is given by:
R1=s⋅l100−l
- The formula for R2 (with end correction) is given by:
R2=s⋅(l+α)100−(l+α)
where s is a constant, l is the length of the wire used, and α is the end correction.
3. Substitute Values:
- Assume l=20 cm and α=1 cm.
- Substitute these values into the equations:
R1=s⋅20100−20=s⋅2080=s4
R2=s⋅(20+1)100−(20+1)=s⋅21100−21=s⋅2179
4. Compare R1 and R2:
- To compare R1 and R2, we can analyze their expressions:
- R1=s4
- R2=s⋅2179
5. Determine the Relationship:
- We need to find out if R2>R1 or R1>R2:
- To do this, we can cross-multiply:
R2>R1⟹s⋅2179>s4
- This simplifies to:
21⋅4>79⟹84>79
- This inequality is true, thus confirming that:
R2>R1
6. Conclusion:
- Therefore, the relationship between the two resistances is:
R2>R1
- Let R1 be the resistance calculated without using the end correction.
- Let R2 be the resistance calculated with the end correction.
- The formula for R1 (without end correction) is given by:
R1=s⋅l100−l
- The formula for R2 (with end correction) is given by:
R2=s⋅(l+α)100−(l+α)
where s is a constant, l is the length of the wire used, and α is the end correction.
- Assume l=20 cm and α=1 cm.
- Substitute these values into the equations:
R1=s⋅20100−20=s⋅2080=s4
R2=s⋅(20+1)100−(20+1)=s⋅21100−21=s⋅2179
- To compare R1 and R2, we can analyze their expressions:
- R1=s4
- R2=s⋅2179
- We need to find out if R2>R1 or R1>R2:
- To do this, we can cross-multiply:
R2>R1⟹s⋅2179>s4
- This simplifies to:
21⋅4>79⟹84>79
- This inequality is true, thus confirming that:
R2>R1
- Therefore, the relationship between the two resistances is:
R2>R1
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Exercise12videos
EXPERIMENTAL PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Exercise -1 PART1videos
EXPERIMENTAL PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP40videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems35videos
GEOMATRICAL OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
Twelve wires of equal length and same cross-section are connected in the form of a cube. If the resistance of each of the wires is R, and the effective resistance between the two diagonal ends is Re, then the ratio RRe is equal to __.
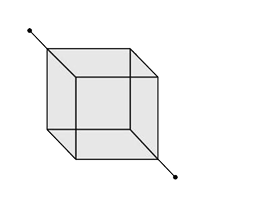 View Solution
View SolutionA meter bridge is setup as shown in figure, to determine an unknown resistance X using a standard 10Ω resistor. The galvanometer shows null point when tapping key is at 52cm mark. The end correctiosnn are 1cm and 2cm respectively for the ends A and B. The determined value of X is
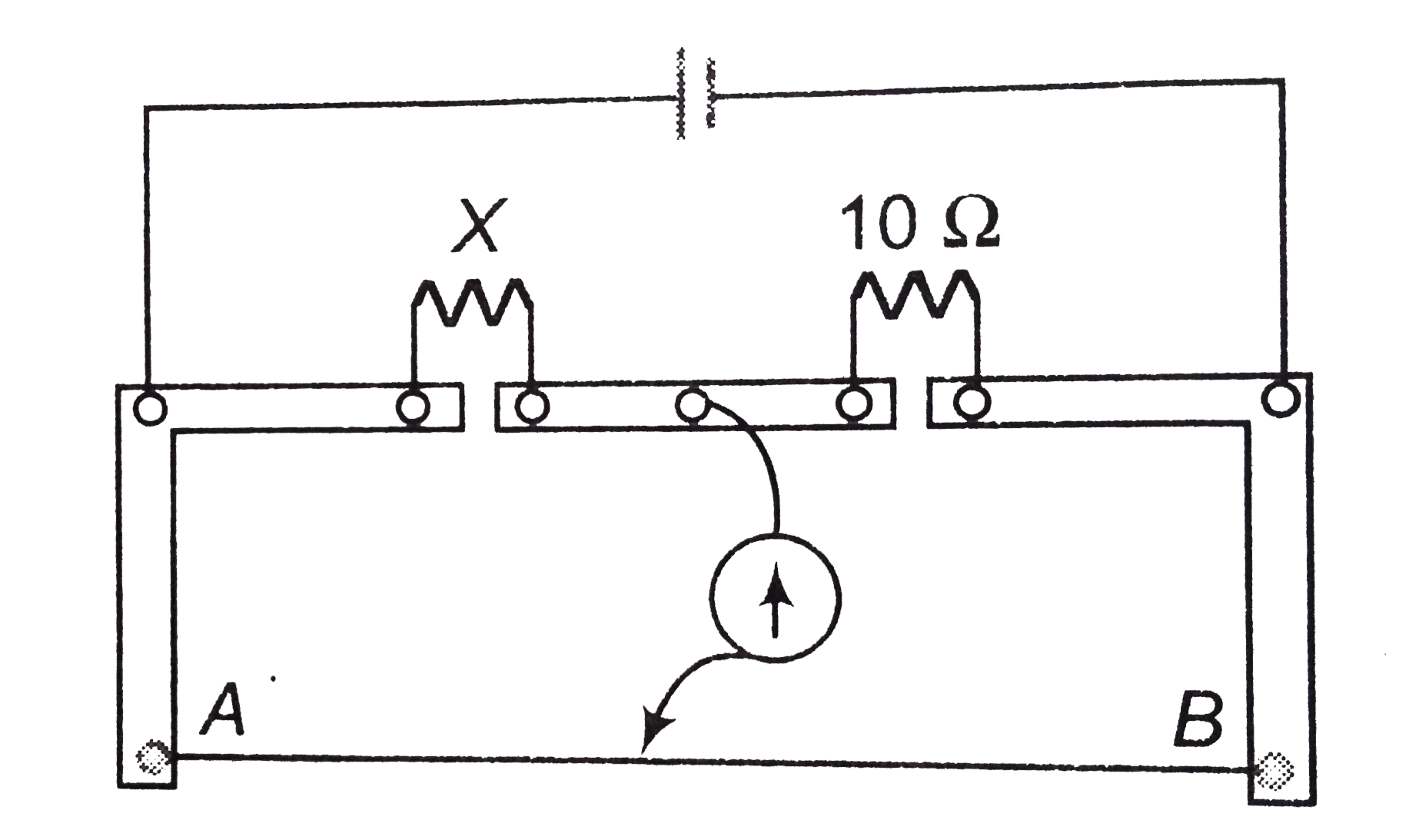 View Solution
View SolutionThe circuit diagram given in the figure shown the experimental setup for the measurement of unknown resistance by using a metre bridge. The wire connected between the points P and Q(PQ = 100 cm) has uniform cross-sectional area and its resistivity is directly proportional to the distance from point P. Null point is obtained with the jockey J with R1andR2 in the gaps. If R1andR2 are interchanged, the jockey has to be displaced through a distance from the previous position along the wire to establish the null point. If the ratio of R1R2=3 , the value of Δ (in cm) is: [Ignore any end corrections]
 View Solution
View SolutionIf the end correction of an open pipe is 0.8 cm, then the inner radius of that pipe will be
View SolutionA meter bridge is set- up as shown in figure, to determine an unknown resistance X using a standard 10Ω resistor. The galvanometer shows null point when tapping - key is at 52cm mark. The end -corrections are 1m and 2cm respectively for the ends A and B. The determined values of X is .
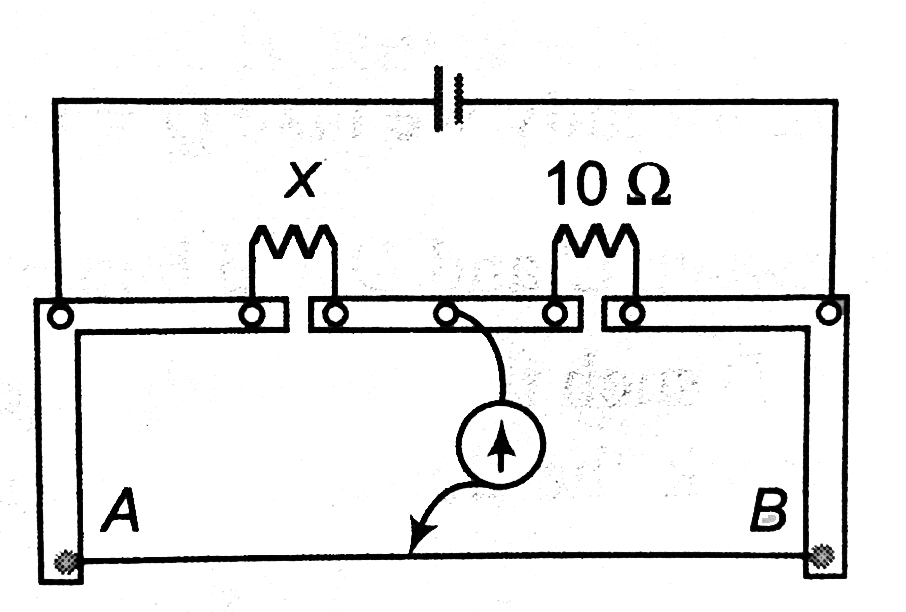
(a) 10.2Omeaga
(b) 10.6Ω
(c) 10.8Ω
(d) 11.1Ω.View SolutionIn the adjoing figure P1andP2 are the pressures in broad and narrow tubes with closed ends. Select the correct option
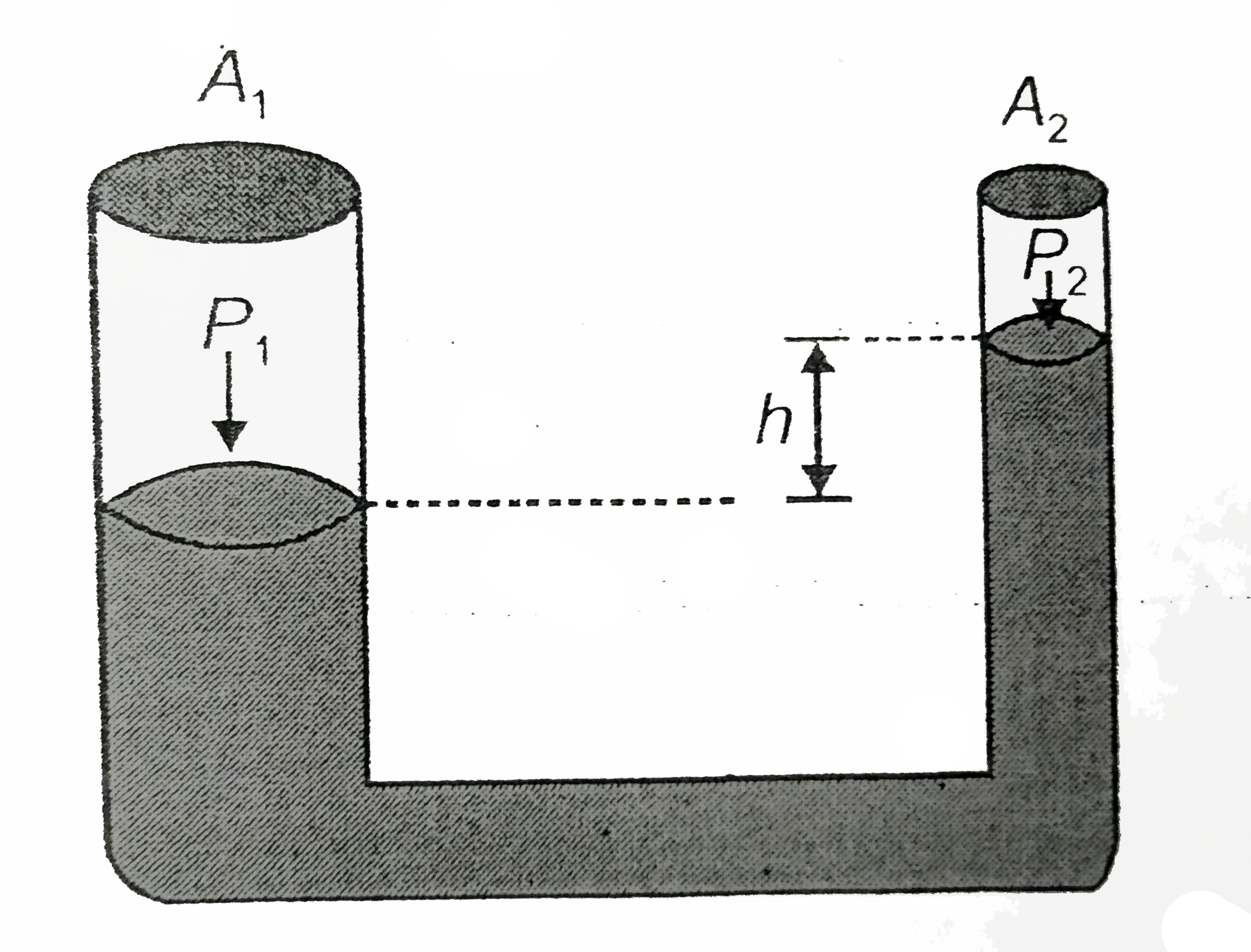 View Solution
View SolutionThe weight of an object on the surface of the Earth is 40 N. Its weight at a height equal to the radius of the Earth is
View Solution

