The initial rate of zero order reaction of the gaseous equation A(g)→2B(g) is 10−2M−1min If the initial concentration of A is 0.1 M what would be concentration of B after 60 seconds ?
0.09 M
0.01 M
0.02 M
0.03 M
The correct Answer is:C
To solve the problem, we need to determine the concentration of B after 60 seconds in a zero-order reaction given by the equation A(g)→2B(g).
1. Understand the Reaction Order:
- The reaction is a zero-order reaction, which means the rate of reaction is constant and does not depend on the concentration of the reactants.
2. Identify the Given Data:
- Initial rate of reaction =10−2M min−1
- Initial concentration of A =0.1M
- Time t=60seconds=1minute
3. Relate Rate to Concentration Change:
- For a zero-order reaction, the rate r can be expressed as:
r=−d(A)dt=k
- Since 2B is produced for every mole of A consumed, we can express the change in concentration of B:
d(B)dt=2k
4. Integrate the Rate Equation:
- Rearranging gives:
d(B)=2kdt
- Integrating from t=0 to t=1 minute:
(B)=2k⋅t
- Here, k=10−2M min−1 and t=1minute.
5. Substitute Values:
- Substitute k and t into the equation:
(B)=2⋅(10−2)⋅(1)=0.02M
6. Final Concentration of B:
- The concentration of B after 60 seconds is 0.02M.
Conclusion:
The concentration of B after 60 seconds is 0.02M.
- The reaction is a zero-order reaction, which means the rate of reaction is constant and does not depend on the concentration of the reactants.
- Initial rate of reaction =10−2M min−1
- Initial concentration of A =0.1M
- Time t=60seconds=1minute
- For a zero-order reaction, the rate r can be expressed as:
r=−d(A)dt=k
- Since 2B is produced for every mole of A consumed, we can express the change in concentration of B:
d(B)dt=2k
- Rearranging gives:
d(B)=2kdt
- Integrating from t=0 to t=1 minute:
(B)=2k⋅t
- Here, k=10−2M min−1 and t=1minute.
- Substitute k and t into the equation:
(B)=2⋅(10−2)⋅(1)=0.02M
- The concentration of B after 60 seconds is 0.02M.
The concentration of B after 60 seconds is 0.02M.
Topper's Solved these Questions
Similar Questions
The rate constant of the reaction A→2B is 1.0×10−3 mol lit−1 min−1, if the initial concentration of A is 1.0 mole lit−1 . What would be the concentration of B after 100 minutes.
View SolutionConsider a reaction A(g)k=0.1M−1min−−−−−−−→2B(g). If initial concentration of A is 0.5 M then select correct graph.
View SolutionThe rate constant for an isomerization reaction, A→B is 4.5×10−3−1min. If the initial concentration of A is 1M, calculate the rate of the reaction after 1h.
View SolutionThe rate constant for an isomerization reaction, A→B is 4.5×10−3−1min. If the initial concentration of A is 1M, calculate the rate of the reaction after 1h.
View SolutionWhat will be the initial rate of a reaction if its rate constant is 10−3−1min and the concentration of reactant is 0.2moldm−3 ? How much of reactant will be converted into Products in 200min?
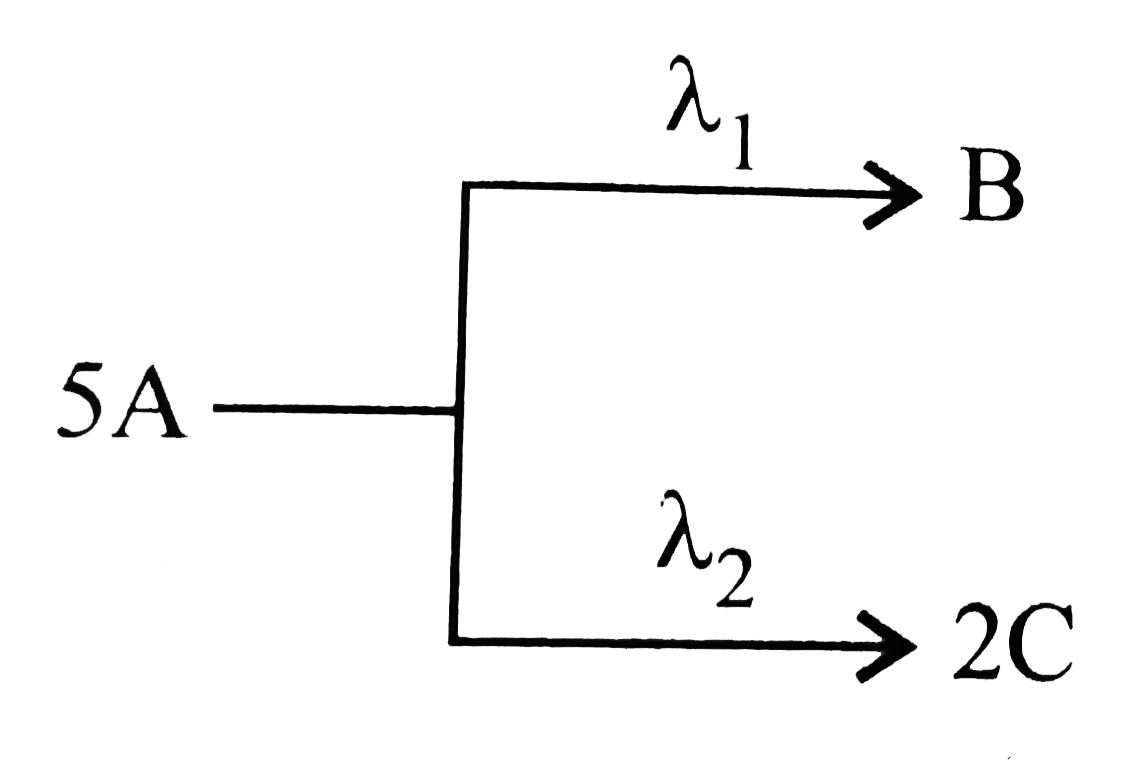
View SolutionA follow parallel path of first-order reactions giving B and C as
If the initial concentration of A is 0.25M, calculate the concentration of C after 5 hr of reaction.
View SolutionThe rate constant of a first order reaction is 3×10−6 per second. If the initial concentration is 0.10M, the initial rate of reaction is
View SolutionThe rate for a first order reaction is 0.6932×10−2molL−1min−1 and the initial concentration of the reactants is 1M, T1/2 is equal to
View SolutionThe rate for a first order reaction is 0.6932×10−2molL−1min−1 and the initial concentration of the reactants is 1M, T1/2 is equal to
View SolutionFor a zero order reaction '[R]0 is the initial concentration
View Solution
