Consider a reaction A(g)k=0.1M−1min−−−−−−−→2B(g). If initial concentration of A is 0.5 M then select correct graph.
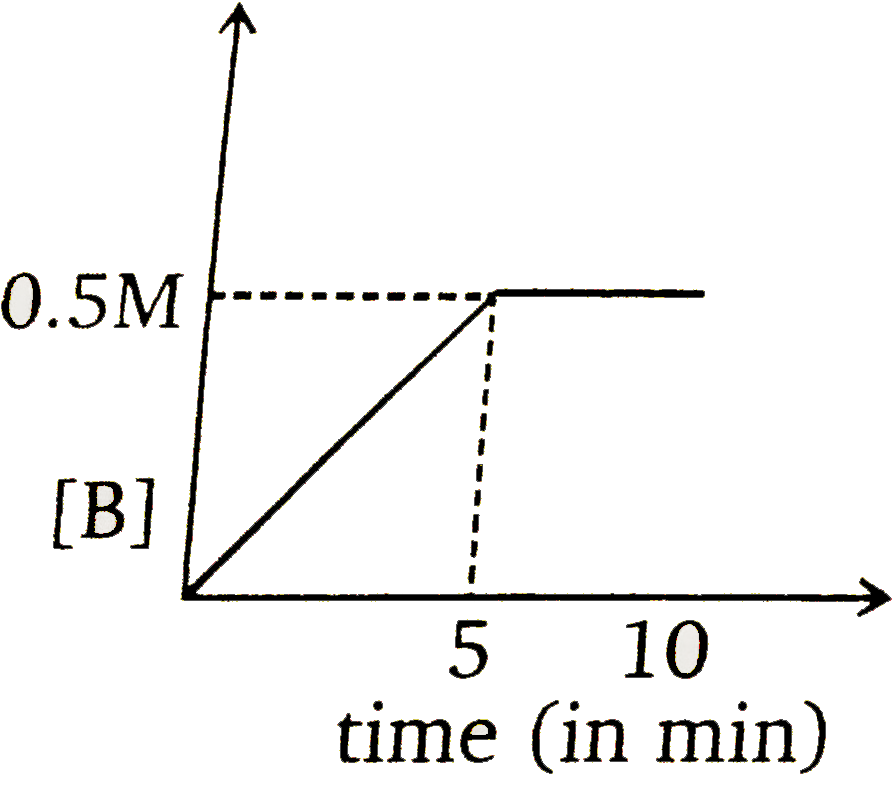
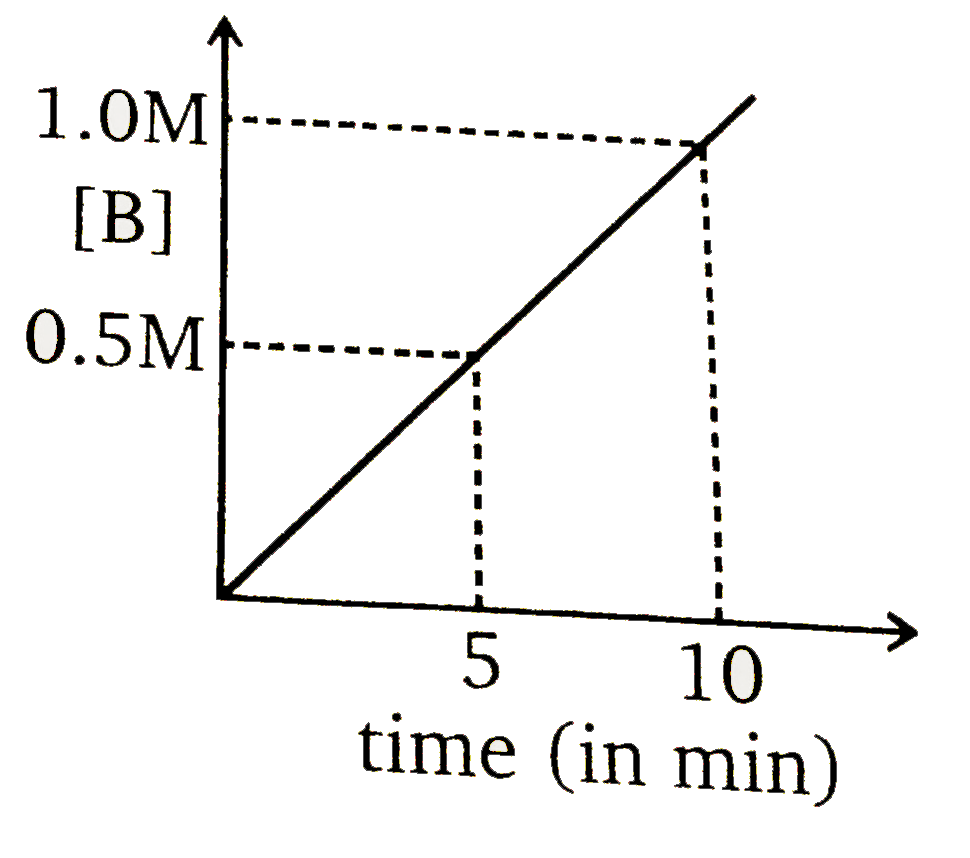
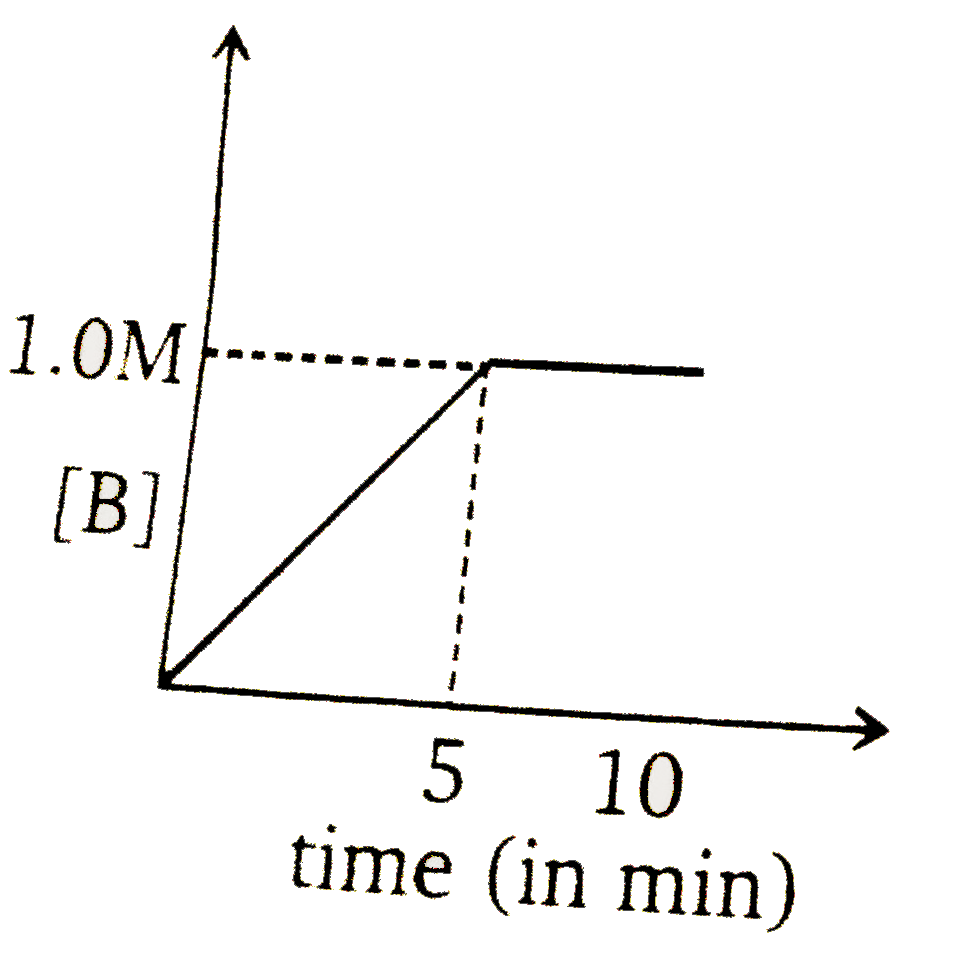
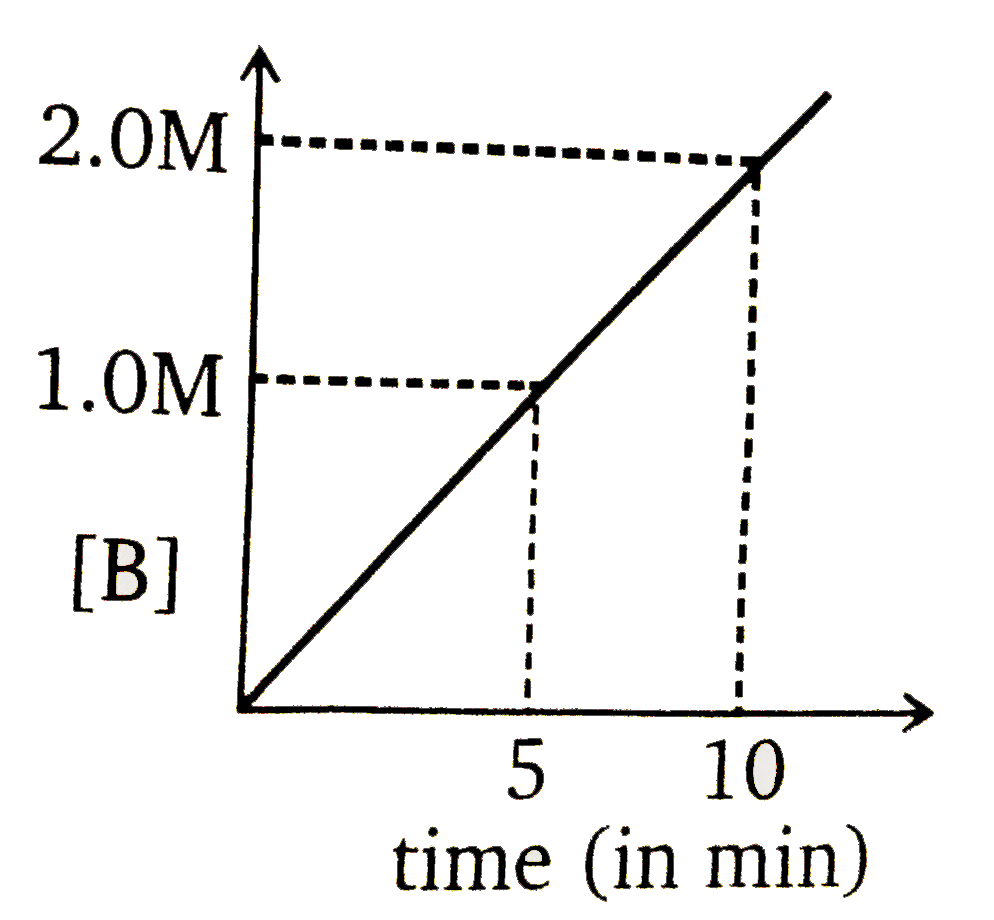
The correct Answer is:C
To solve the problem, we need to analyze the given reaction and the information provided. The reaction is:
A(g)k=0.1M min−1→2B(g)
Step 1: Determine the Order of the Reaction
The rate constant k is given as 0.1M min−1. The units of k can help us determine the order of the reaction. The general unit of k is given by:
Units of k=M1−n⋅s−1
Here, since the unit of k is M min−1, we can express it in terms of seconds:
M min−1=M⋅min−1=M⋅(160s)−1=M⋅s−1
From the unit M min−1, we can deduce that:
1−n=1⟹n=0
Thus, the reaction is a zero-order reaction.
Step 2: Write the Rate Law for Zero-Order Reaction
For a zero-order reaction, the rate of reaction is constant and can be expressed as:
Rate=k=0.1M min−1
Step 3: Calculate the Change in Concentration Over Time
For a zero-order reaction, the change in concentration of A over time can be described by the equation:
(A)=(A0)−kt
Where:
- (A0) is the initial concentration of A (0.5 M),
- k is the rate constant (0.1 M/min),
- t is the time in minutes.
Step 4: Calculate Concentration of A at t=5 minutes
Substituting the known values into the equation:
(A)=0.5M−(0.1M min−1)(5min)
(A)=0.5M−0.5M=0M
This means that at t=5 minutes, all of A has reacted.
Step 5: Calculate Concentration of B
Since the stoichiometry of the reaction shows that 1 mole of A produces 2 moles of B:
If A is completely consumed, then (B)=2×moles of A reacted
At t=5 minutes, 0.5M of A has reacted, thus:
(B)=2×0.5M=1M
Step 6: Determine the Graph
At t=5 minutes, the concentration of B is 1M and A is 0M. Therefore, we need to select the graph that shows (B)=1M at t=5 minutes and indicates that the reaction has stopped (i.e., no further increase in B) after this point.
Conclusion
The correct graph is the one that shows:
- At t=5 minutes, (B)=1M
- No further increase in (B) after t=5 minutes.
The rate constant k is given as 0.1M min−1. The units of k can help us determine the order of the reaction. The general unit of k is given by:
For a zero-order reaction, the rate of reaction is constant and can be expressed as:
For a zero-order reaction, the change in concentration of A over time can be described by the equation:
- (A0) is the initial concentration of A (0.5 M),
- k is the rate constant (0.1 M/min),
- t is the time in minutes.
Substituting the known values into the equation:
(A)=0.5M−0.5M=0M
Since the stoichiometry of the reaction shows that 1 mole of A produces 2 moles of B:
At t=5 minutes, the concentration of B is 1M and A is 0M. Therefore, we need to select the graph that shows (B)=1M at t=5 minutes and indicates that the reaction has stopped (i.e., no further increase in B) after this point.
The correct graph is the one that shows:
- At t=5 minutes, (B)=1M
- No further increase in (B) after t=5 minutes.
Similar Questions
The initial rate of zero order reaction of the gaseous equation A(g)→2B(g) is 10−2M−1min If the initial concentration of A is 0.1 M what would be concentration of B after 60 seconds ?
View SolutionFor a reaction Akr=0.6M−1min−−−−−−−−→2B
starting with 1 M of 'A' only, concentration of B (in M) after 100 sec. and 200 sec. is respectively?
View SolutionThe rate constant for an isomerization reaction, A→B is 4.5×10−3−1min. If the initial concentration of A is 1M, calculate the rate of the reaction after 1h.
View SolutionThe rate constant for an isomerization reaction, A→B is 4.5×10−3−1min. If the initial concentration of A is 1M, calculate the rate of the reaction after 1h.
View SolutionConsider the reaction :
P(g)+2Q(g)KC=1012⇐===⇒R(g)+S(g)Initial conc.2M4M00
then select correct statement(s)
View SolutionFor a particular reaction (A → B) the rate constant is 0.693(min)−1 If the initial concentration of the reactant, A is 1 M, then the rate of reaction after 1 minute will be
View SolutionIn a first-order reaction A→B, if K is the rate constant and initial concentration of the reactant is 0.5M, then half-life is
View SolutionIn a first-order reaction A→B, if k is rate constant and initial concentration of the reactant A is 0.5 M then the half-life is:
View SolutionConsider a reaction A→B+C . The initial concentration of A was reduced form 2Mto 1M in 1h and form 1M to 0.25M in 2h, the order of the reaction is
(a) 1
(b) 0
(c) 2
(d) 3
View SolutionConsider reaction in which reactant R is converted into product P: R→P. When the initial concentration of R′ is 0.5M The half life of the reaction is 20 minute. When the initial concentration is increased to 1.3 M, the half life decreases to 7.69 minute.
Q. What is the rate canstant of the reaction?
View Solution
