One mole of an ideal monoatomic gas is caused to go through the cycle shown in figure. Then the change in the internal energy of gas from a to b and b to c is respectively
9P∘V∘2,6RT∘
9P∘V∘2,10RT∘
15P∘V∘2,6RT∘
15P∘V∘2,10RT∘
The correct Answer is:A
To solve the problem of finding the change in internal energy of an ideal monoatomic gas as it goes through the cycle from A to B and from B to C, we can follow these steps:
Step 1: Understand the Internal Energy Change Formula
The change in internal energy (ΔU) for an ideal gas can be calculated using the formula:
ΔU=f2nRΔT
where:
- f is the degrees of freedom (for a monoatomic gas, f=3),
- n is the number of moles,
- R is the universal gas constant,
- ΔT is the change in temperature.
Step 2: Analyze the Process from A to B
For the process from A to B:
- Since it is a monoatomic gas, f=3.
- The change in internal energy can be expressed as:
ΔUA→B=32nR(TB−TA)
- We need to find the temperatures at points A and B using the ideal gas law PV=nRT.
Assuming at point A:
- PA=P0
- VA=V0
Then, using the ideal gas law:
P0V0=nRTA⟹TA=P0V0nR
At point B:
- PB=P0
- VB=4V0
Using the ideal gas law again:
P0(4V0)=nRTB⟹TB=P0(4V0)nR
Step 3: Calculate ΔU from A to B
Now, substituting the values of TA and TB:
ΔUA→B=32nR(P0(4V0)nR−P0V0nR)
=32nR(3P0V0nR)=92P0V0
Step 4: Analyze the Process from B to C
For the process from B to C:
- At point C, let’s assume:
- PC=2P0
- VC=4V0
Using the ideal gas law:
2P0(4V0)=nRTC⟹TC=8P0V0nR
Now, we can calculate ΔU from B to C:
ΔUB→C=32nR(TC−TB)
Substituting the values:
ΔUB→C=32nR(8P0V0nR−4P0V0nR)
=32nR(4P0V0nR)=6P0V0
Step 5: Final Values
Thus, the changes in internal energy are:
- From A to B: ΔUA→B=92P0V0
- From B to C: ΔUB→C=6P0V0
Summary
The change in internal energy of the gas from A to B is 92P0V0 and from B to C is 6P0V0.
The change in internal energy (ΔU) for an ideal gas can be calculated using the formula:
ΔU=f2nRΔT
where:
- f is the degrees of freedom (for a monoatomic gas, f=3),
- n is the number of moles,
- R is the universal gas constant,
- ΔT is the change in temperature.
For the process from A to B:
- Since it is a monoatomic gas, f=3.
- The change in internal energy can be expressed as:
ΔUA→B=32nR(TB−TA)
- We need to find the temperatures at points A and B using the ideal gas law PV=nRT.
- PA=P0
- VA=V0
P0V0=nRTA⟹TA=P0V0nR
- PB=P0
- VB=4V0
P0(4V0)=nRTB⟹TB=P0(4V0)nR
Now, substituting the values of TA and TB:
ΔUA→B=32nR(P0(4V0)nR−P0V0nR)
=32nR(3P0V0nR)=92P0V0
For the process from B to C:
- At point C, let’s assume:
- PC=2P0
- VC=4V0
2P0(4V0)=nRTC⟹TC=8P0V0nR
ΔUB→C=32nR(TC−TB)
Substituting the values:
ΔUB→C=32nR(8P0V0nR−4P0V0nR)
=32nR(4P0V0nR)=6P0V0
Thus, the changes in internal energy are:
- From A to B: ΔUA→B=92P0V0
- From B to C: ΔUB→C=6P0V0
The change in internal energy of the gas from A to B is 92P0V0 and from B to C is 6P0V0.
Topper's Solved these Questions
Similar Questions
One mole of an ideal mono-atomic gas is caused to go through the cycle shown in the figure below. Then the change in the internal enegry in expanding the gas from a to c along the path abc is:

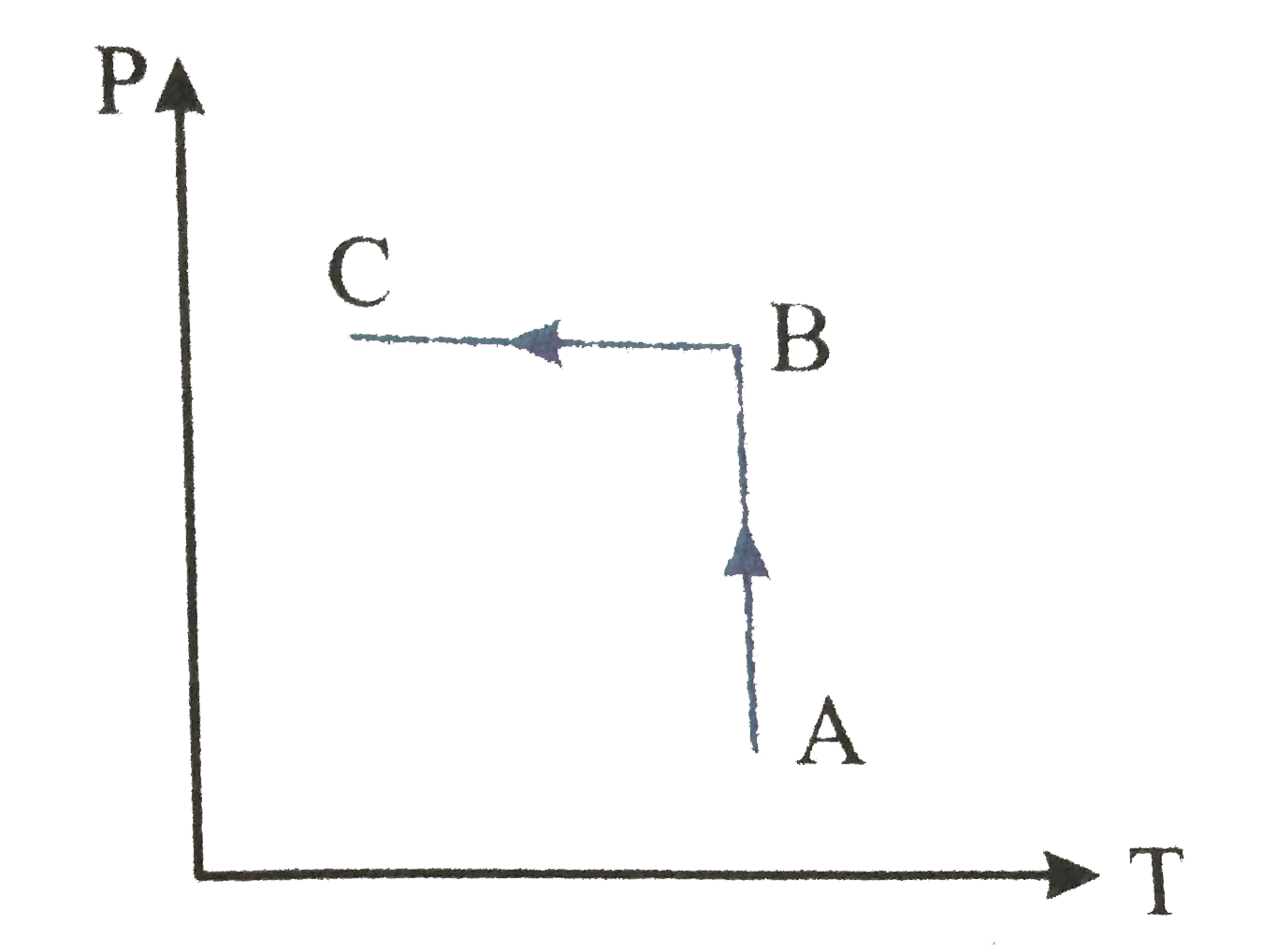
View SolutionOne mole of an ideal monoatomic gas is taken through a cyclic process as shown. Choose the correct option(s).
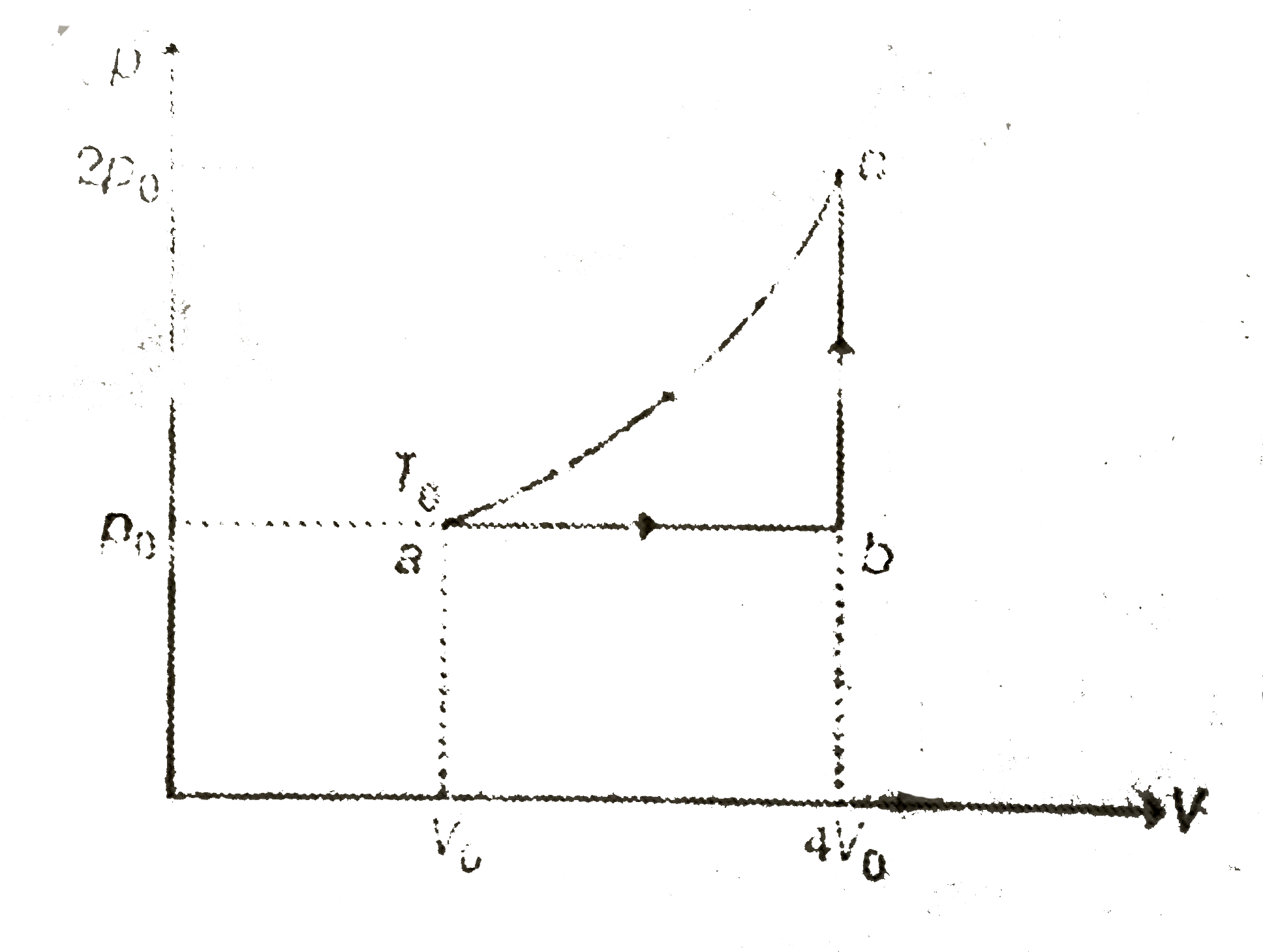
View SolutionIdeal gas is taken through the process shown in the figure :
View SolutionIdeal gas is taken through the process shown in the figure :

View SolutionA sample of an ideal monoatomic gas is taken round the cycle ABCA as shown in the figure the work done during the cycle is

View SolutionAn ideal monoatomic gas is carried around the cycle ABCDA as shown in the figure. The efficiency of the gas cycle is

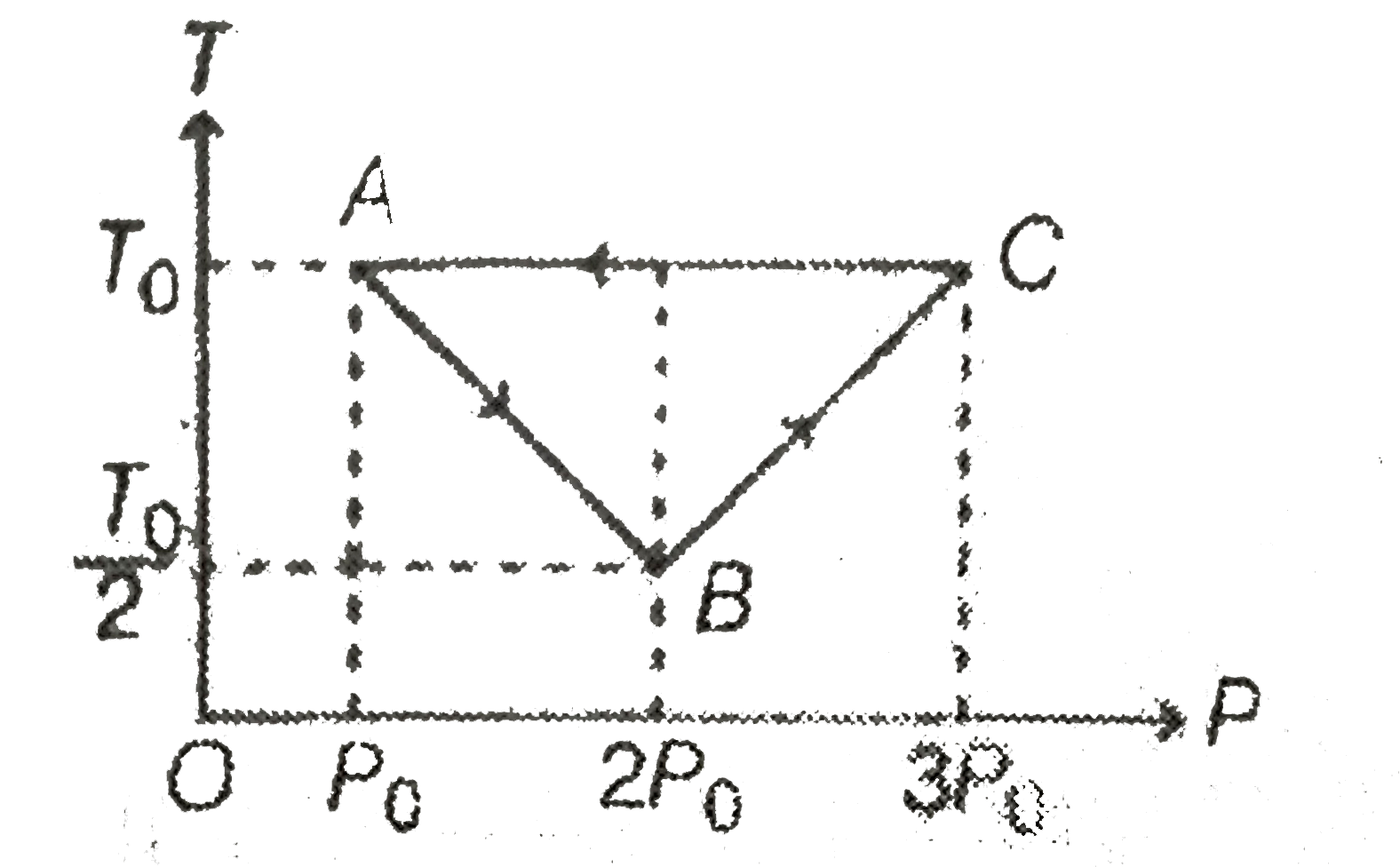
View SolutionOne mole of an ideal monatomic gas (intial temperature T0) is made to go through the cycle abca as shown in the figure. If U denotes the internal energy, then choose the correct alternatives
View SolutionAn ideal monoatomic gas is carried around the cycle ABCDA as shown in the figure. The efficiency of the cycle is ltBrgt
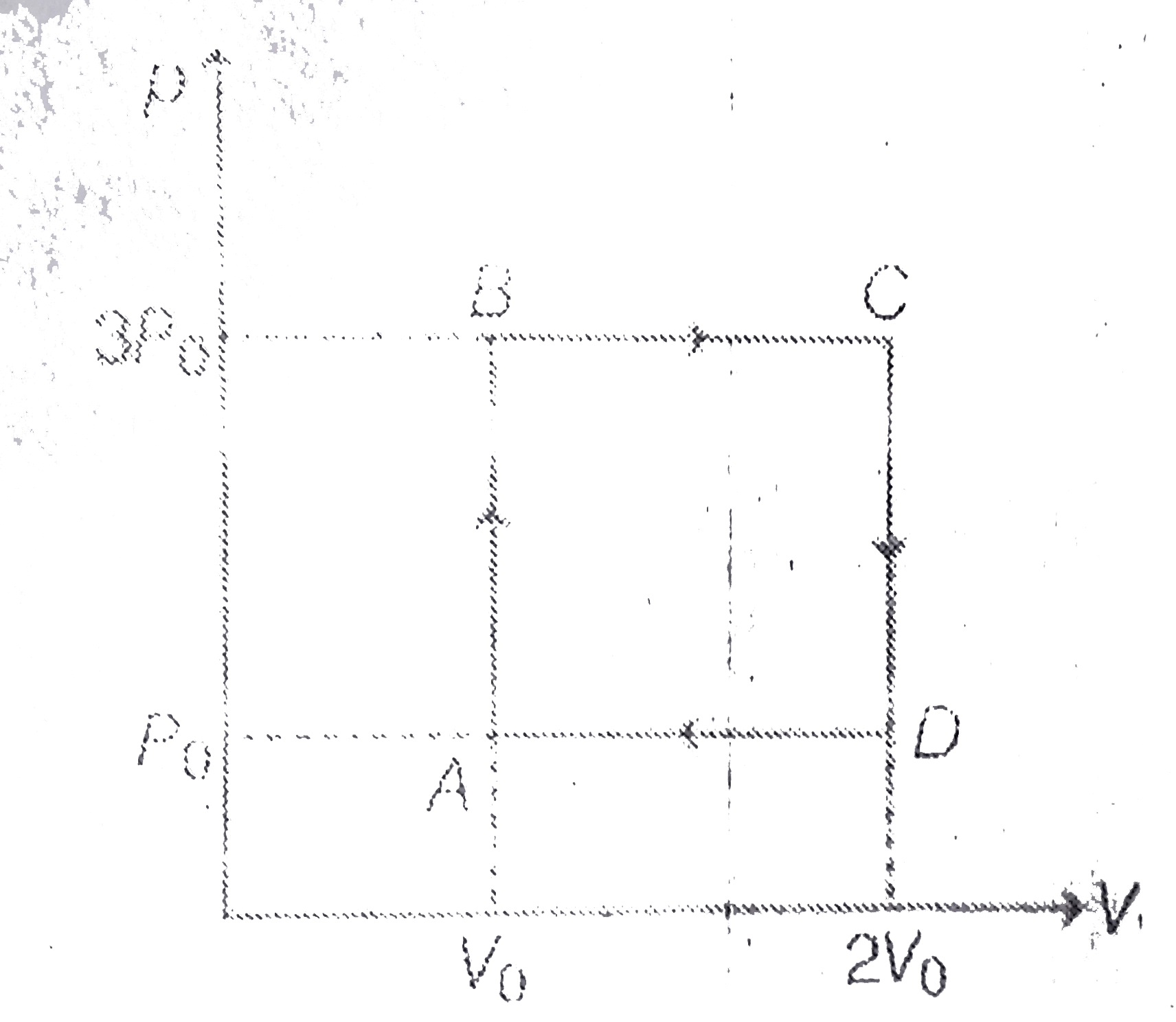
View Solution0.5 moles of an ideal monoatomic gas undergoes a thermodynamic process from A to B as shown in figure. The change in internal energy of the gas during the process from A to B is
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is (γ=3/5)
View Solution
