Question

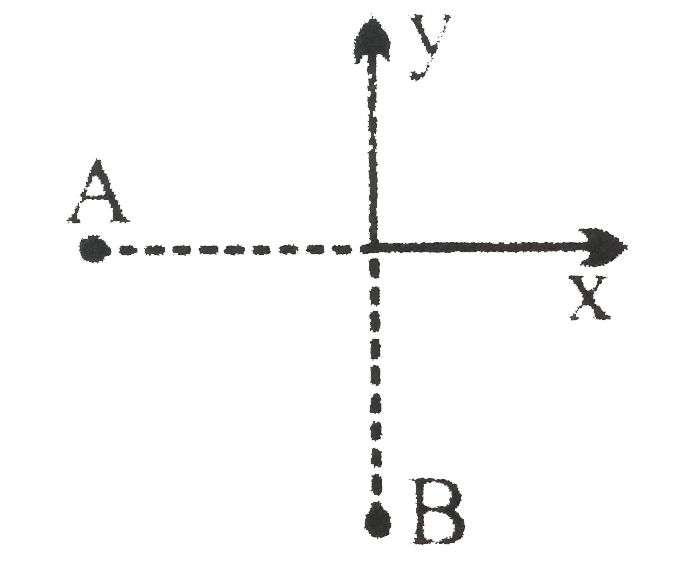
Two particles A and B are performing SHM along x and y-axis respectively with equal amplitude and frequency of $2cm$ and $1Hz$ respectively. Equilibrium positions of the particles A and B are at the coordinates $[3cm,0]$ and $(0,4cm)$ respectively. At $t=0,B$ is at its equilibrium position and moving towards the origin, while A is nearest to the origin and moving away from the origin-
Equation of motion of particle B can be written as-

Answer

10

Explanation

To derive the equation of motion for particle B, we will follow these steps:

Step 1: Understand the parameters of SHM
Given:
- Amplitude (A) = 2 cm
- Frequency (f) = 1 Hz
- Equilibrium position of particle B = (0, 4 cm)

Step 2: Determine the angular frequency (ω)
The angular frequency (ω) can be calculated using the formula:
\( \omega = 2\pi f \)
Substituting the given frequency:
\( \omega = 2\pi \times 1 = 2\pi \text{ rad/s} \)

Step 3: Write the general equation of motion for SHM
The general equation of motion for a particle performing SHM is given by:
\( y(t) = A \sin(\omega t + \phi) \)
Where:
- \(y(t)\) is the displacement from the equilibrium position,
- \(A\) is the amplitude,
- \(\omega\) is the angular frequency,
- \(\phi\) is the phase constant.

Step 4: Determine the phase constant (φ)
At \(t = 0\), particle B is at its equilibrium position (y = 4 cm) and moving towards the origin. This means that the sine function should start at 0 and be negative (since it is moving downwards). Therefore, we can set:
\( \phi = 0 \)
Thus, the equation simplifies to:
\( y(t) = A \sin(\omega t) \)

Step 5: Substitute the values into the equation
Substituting the values of amplitude and angular frequency:
\( y(t) = 2 \sin(2\pi t) \)

Step 6: Adjust for the equilibrium position
Since the equilibrium position of particle B is at (0, 4 cm), we need to adjust the equation to reflect this:
\( y(t) = 4 - 2 \sin(2\pi t) \)
This indicates that when \(y = 4\), the particle is at its equilibrium position, and as it moves downwards, the sine function will decrease.

Final Equation of Motion for Particle B
Thus, the equation of motion for particle B can be written as:
\( y(t) = 4 - 2 \sin(2\pi t) \)

---