A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is 120 Hz. If the movable support is pushed to the right by 10 cm so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate ?
 .
.
The correct Answer is:240Hz.
As end A is free so antinode is formed
∴l=λ14
Now if support is pushed to right by 10cm so that node is formed at joint
∴L=λ2⇒(λ2=λ12)
As V is same so if wavelength is halfed frequency will be doubled i.e. 240Hz
Topper's Solved these Questions
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 1 PART II
31 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 2 PART I
21 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Board Level Exercise
27 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 3 PART I
19 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Advanced Level Problems
8 Videos
Similar Questions
A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in figure. The thread goes over a fixed pulley and supports a wieght to produce a tension. The lowest frequency with which the heavy sting resonates is 120Hz. If the movable support is pushed to the right by 20cm so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate?

View SolutionA light string is tied at one end to a fixed support and to a heavy string of equal length L at the other end as shown in figure. A block of mass m is tied to the free end of heavy string. Mass per unit length of the strings are μ and 9μ and the tension is T. Find the possible values of frequencies such that junction of two wire point A is a node.

View Solution
Knowledge Check
A string of negligible mass going over a clamped pulley of mass m supports a block of M as shown in the figure. the force on the pulley by the clamp is given by:
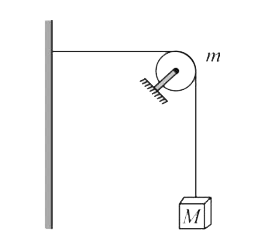 A√2MgB√2mgC√(M+m)2+m2gD√(M+m)2+M2g
A√2MgB√2mgC√(M+m)2+m2gD√(M+m)2+M2g
A spring with one end attached to a mass and the other to a right support is stretched and released
View SolutionA heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
View SolutionA heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
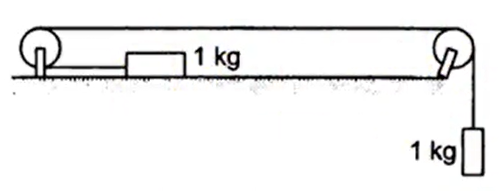
View SolutionCalculate the tension in the string shown in figure. The pulley and the string are light and all surfaces are frictionless. Take g=10 m/s2.
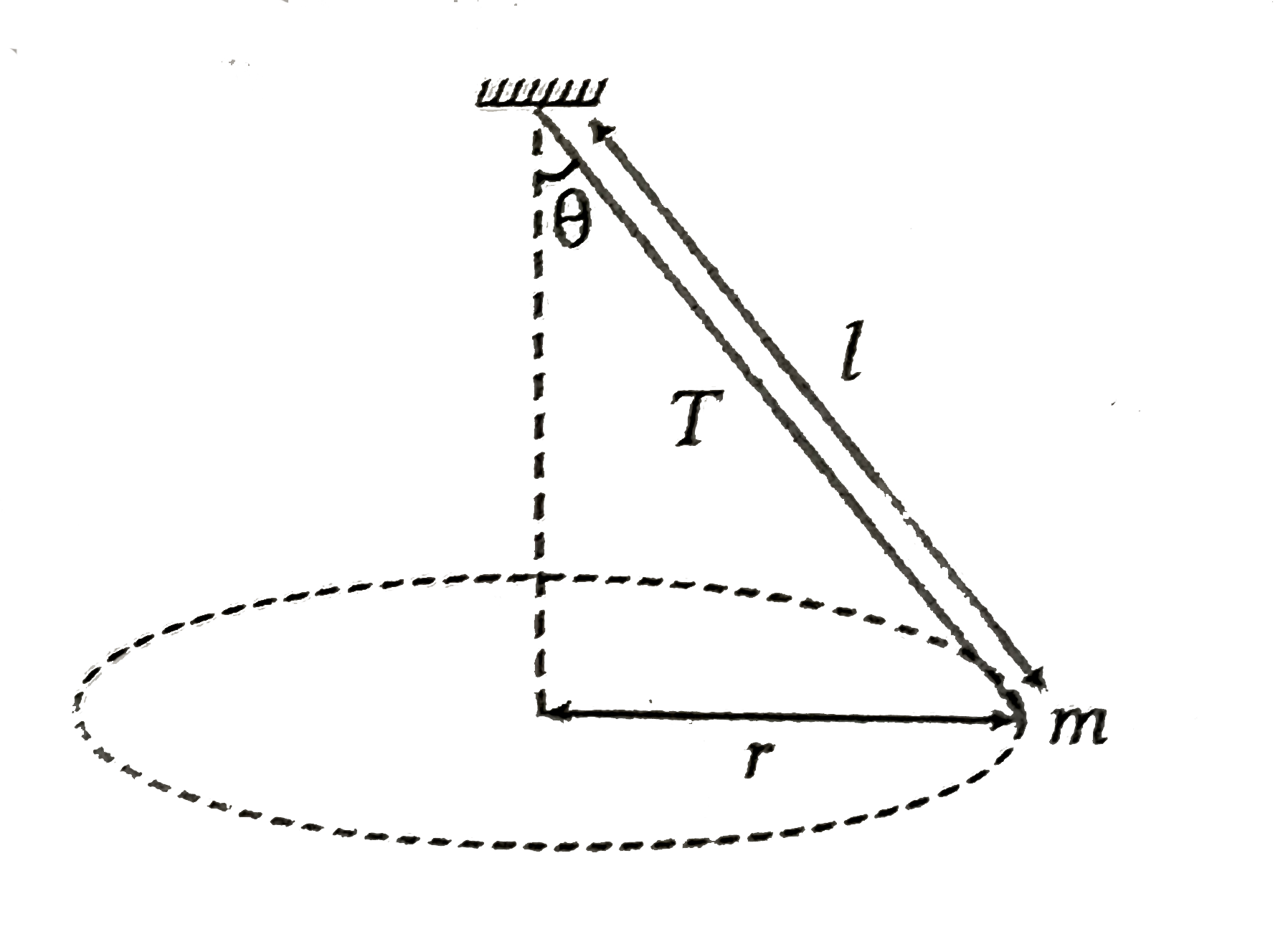
View SolutionA string of lenth l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
View SolutionA 1m long rope, having a mass of 40g, is fixed at one end and is tied to a light string at the other end. The tension in the string in 400N. Find the wavelength in second overtone (in cm).
View SolutionA string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by

View Solution
