One end of a taut string of length 3 m along the x-axis is fixed at x = 0. The speed of the waves in the string is 100 m s−1. The other end of the string is vibrating in the y direction so that stationary waves are set up in the string. The possible waveform(s) of these stationary waves is(are)
y(t)=Asin'πx6cos'50πt3
y(t)=Asin'πx3cos'100πt3
y(t)=Asin'5πx6cos'50πt3
y(t)=Asin'5πx6cos250πt
The correct Answer is:A,C,D
V=100m/s
Possible modes of vibration
l=(2n+1)λ4
λ=12(2n+1)m
k=2πλ=2π12/(2n+1)=(2n+1)π6
ω=vk=100(2n+1)π6=(2n+1)50π3
If n=0,k=π6,ω=50π3
n=1,k=5π6,ω=250π3
n=7,k=5π2,ω=250π
Topper's Solved these Questions
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 3 PART II
7 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 2 PART IV
9 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 3 PART I
19 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Advanced Level Problems
8 Videos
Similar Questions
Knowledge Check
One end of a taut string of length 3m along the x-axis is fixed at x=0. The speed of the waves in the string is 100ms−1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible wavelength(s) of these sationary waves is (are)
Ay(t)=Asin(2πx)6cos(50πt)3By(t)=Asin(πx)3cos(100πt)3Cy(t)=Asin(5πx)6cos(255πt)3Dy(t)=Asin(5πx)2cos250πt
A string of length 1 m and mass 5 g is fixed at both ends. The tension in the string is 8.0 N. The string is set into vibration using an external vibrator of frequency 100 Hz. The separation between successive nodes on the string is close to :
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
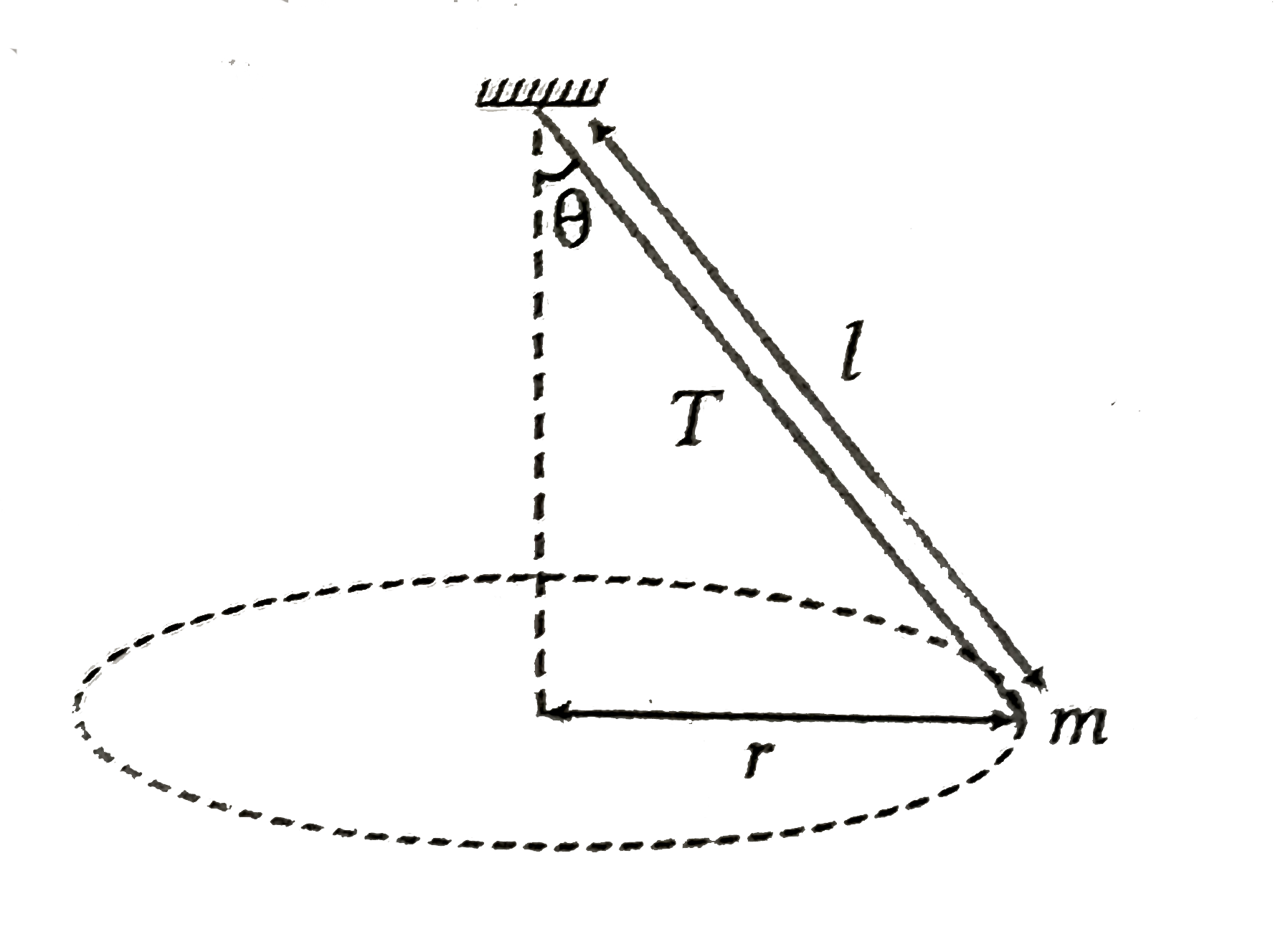
View SolutionA string of lenth l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
View SolutionThe extension in a string obeying Hooke's law is x. The speed of transverse wave in the stretched string is v. If the extension in the string is increased to 1.5x, the speed of transverse wave will be
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionFor a string clamped at both its ends, which of the following wave equation is lare valid for a stationary wave set up in It? (Origin is at one end of string)
View SolutionA stretched string is fixed at both its ends. Three possible wavelengths of stationary wave patterns that can be set up in the string are 90 cm, 60 cm and 45 cm. the length of the string may be
View Solution
