A square frame carrying a current I=0.9A is located in the same plane as a long straght wire carrying a current, I0=5.0A. The frame side has a length a=8.0cm. The axis of the frame passing thorugh the midpoints of opposite sides is parallel to the wire and is separated from it by the distance which is η=1.5 times greater than the side of the frame. FInd:
(a) Ampere force acting on the frame,
(b) the mechnical work to be performed in order to turn the frame throguh 180∘ about its axis, with the currents maintained constant.
The correct Answer is:A, B
To solve the problem, we will break it down into two parts: (a) calculating the Ampere force acting on the square frame, and (b) determining the mechanical work required to turn the frame through 180 degrees about its axis while maintaining the currents constant.
Given Data:
- Current in the square frame, I=0.9A
- Current in the straight wire, I0=5.0A
- Side length of the square frame, a=8.0cm=0.08m
- Distance between the wire and the frame, d=1.5×a=1.5×0.08m=0.12m
Part (a): Ampere Force Acting on the Frame
1. Calculate the Magnetic Field due to the Straight Wire:
The magnetic field B at a distance d from a long straight wire carrying current I0 is given by:
B=μ0I02πd
where μ0=4π×10−7T⋅m/A (permeability of free space).
Substituting the values:
B=4π×10−7×5.02π×0.12=2×10−60.12≈1.67×10−5T
2. Calculate the Force on Each Side of the Frame:
The force F on a current-carrying conductor in a magnetic field is given by:
F=I⋅L⋅B⋅sin(θ)
where θ is the angle between the current direction and the magnetic field. For the sides of the frame parallel to the wire, θ=90∘ (so sin(90∘)=1).
Each side of the frame has a length a, so the force on the two sides parallel to the wire is:
Fparallel=2⋅I⋅a⋅B
Substituting the values:
Fparallel=2⋅0.9⋅0.08⋅1.67×10−5≈2.4×10−6N
3. Calculate the Net Force:
The forces on the two sides of the frame that are perpendicular to the wire will cancel each other out since they are equal in magnitude and opposite in direction. Therefore, the net force acting on the frame is:
Fnet=Fparallel=2.4×10−6N
Part (b): Mechanical Work to Turn the Frame
1. Calculate the Torque on the Frame:
The torque τ on a current loop in a magnetic field is given by:
τ=n⋅I⋅A⋅B
where n is the number of turns (1 for a single loop), A is the area of the loop, and B is the magnetic field.
The area A of the square frame is:
A=a2=(0.08)2=0.0064m2
Substituting the values:
τ=1⋅0.9⋅0.0064⋅1.67×10−5≈8.06×10−10N⋅m
2. Calculate the Work Done to Rotate the Frame:
The work done W to rotate the frame through an angle θ is given by:
W=τ⋅θ
where θ must be in radians. For 180∘:
θ=πradians
Substituting the values:
W=8.06×10−10⋅π≈2.53×10−9J
Final Answers:
(a) The Ampere force acting on the frame is approximately 2.4×10−6N.
(b) The mechanical work to be performed in order to turn the frame through 180∘ is approximately 2.53×10−9J.
- Current in the square frame, I=0.9A
- Current in the straight wire, I0=5.0A
- Side length of the square frame, a=8.0cm=0.08m
- Distance between the wire and the frame, d=1.5×a=1.5×0.08m=0.12m
The magnetic field B at a distance d from a long straight wire carrying current I0 is given by:
B=μ0I02πd
where μ0=4π×10−7T⋅m/A (permeability of free space).
B=4π×10−7×5.02π×0.12=2×10−60.12≈1.67×10−5T
The force F on a current-carrying conductor in a magnetic field is given by:
F=I⋅L⋅B⋅sin(θ)
where θ is the angle between the current direction and the magnetic field. For the sides of the frame parallel to the wire, θ=90∘ (so sin(90∘)=1).
Fparallel=2⋅I⋅a⋅B
Fparallel=2⋅0.9⋅0.08⋅1.67×10−5≈2.4×10−6N
The forces on the two sides of the frame that are perpendicular to the wire will cancel each other out since they are equal in magnitude and opposite in direction. Therefore, the net force acting on the frame is:
Fnet=Fparallel=2.4×10−6N
The torque τ on a current loop in a magnetic field is given by:
τ=n⋅I⋅A⋅B
where n is the number of turns (1 for a single loop), A is the area of the loop, and B is the magnetic field.
A=a2=(0.08)2=0.0064m2
τ=1⋅0.9⋅0.0064⋅1.67×10−5≈8.06×10−10N⋅m
The work done W to rotate the frame through an angle θ is given by:
W=τ⋅θ
where θ must be in radians. For 180∘:
θ=πradians
W=8.06×10−10⋅π≈2.53×10−9J
(a) The Ampere force acting on the frame is approximately 2.4×10−6N.
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3
18 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3 COMPREHENSION-1
5 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-1
15 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
A square frame carrying a current I=0.90A is located in the same plane as a long straight wire carrying a current I0=5A, The frame side has a length a=8cm. The axis of the frame passing through the mid-point of the opposite sides is parrallel to the wire and is separated form it by a distance h=15 times greater tahn the side of the frame.
Find:
(a) ampere force acting on the frame.
(b) The machanical work to be performed in order to turn the frmae through 180∘ about its axis, with the current maintained constant.
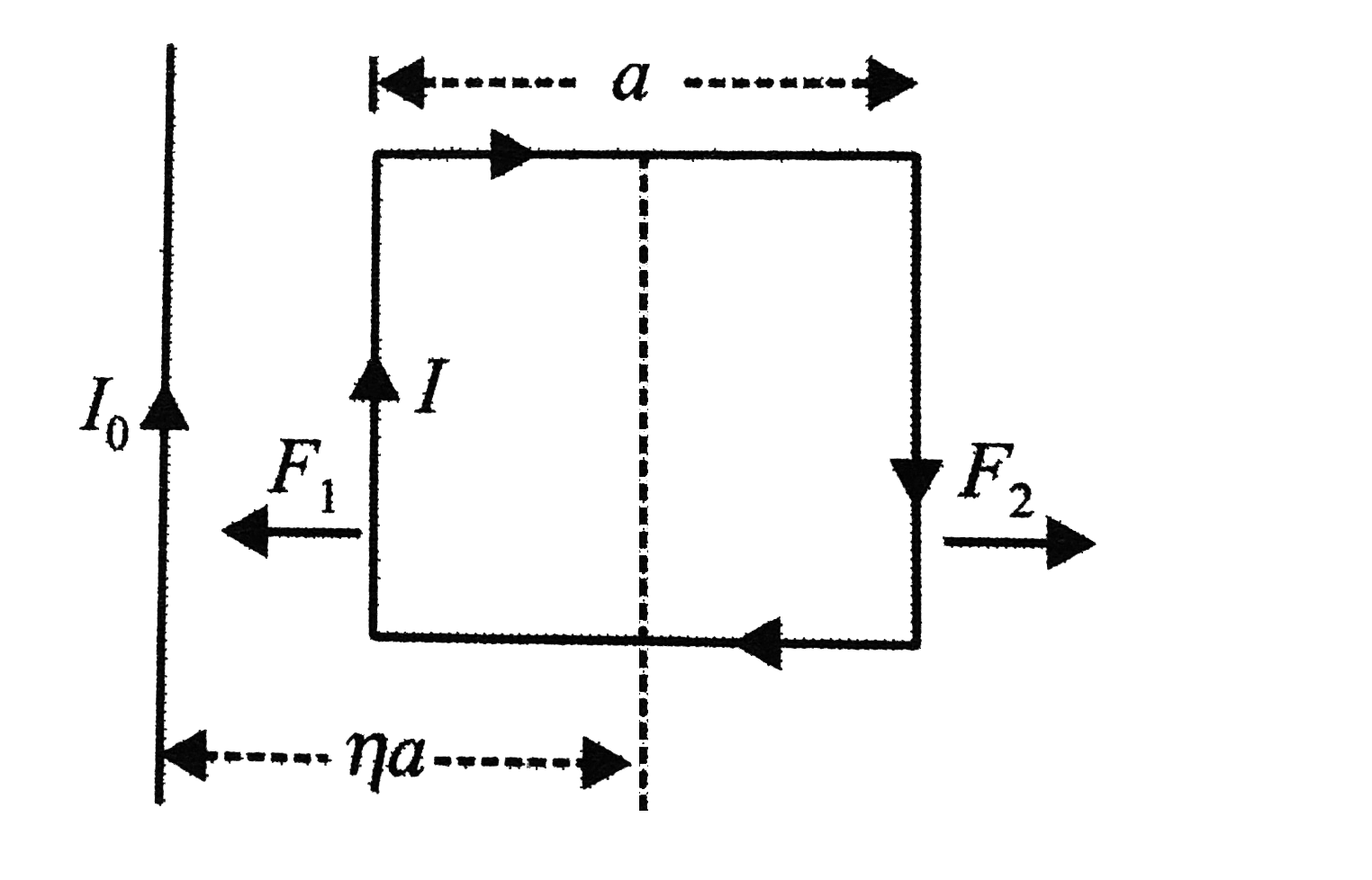
View SolutionA square loop ABCD , carrying a current I, is placed near and coplanar with a long straight conductor XY carrying a current I.

View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
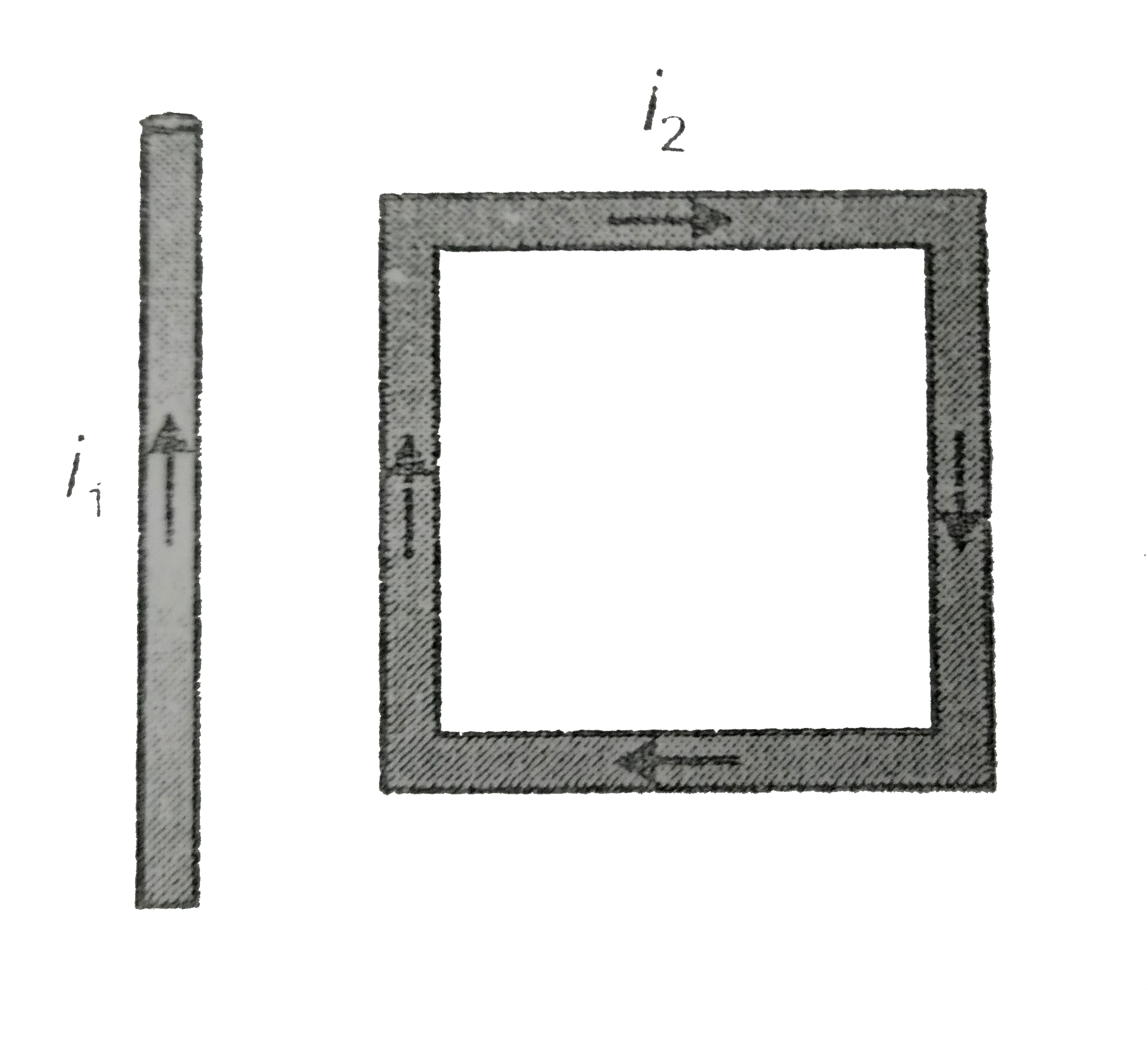
View SolutionA rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
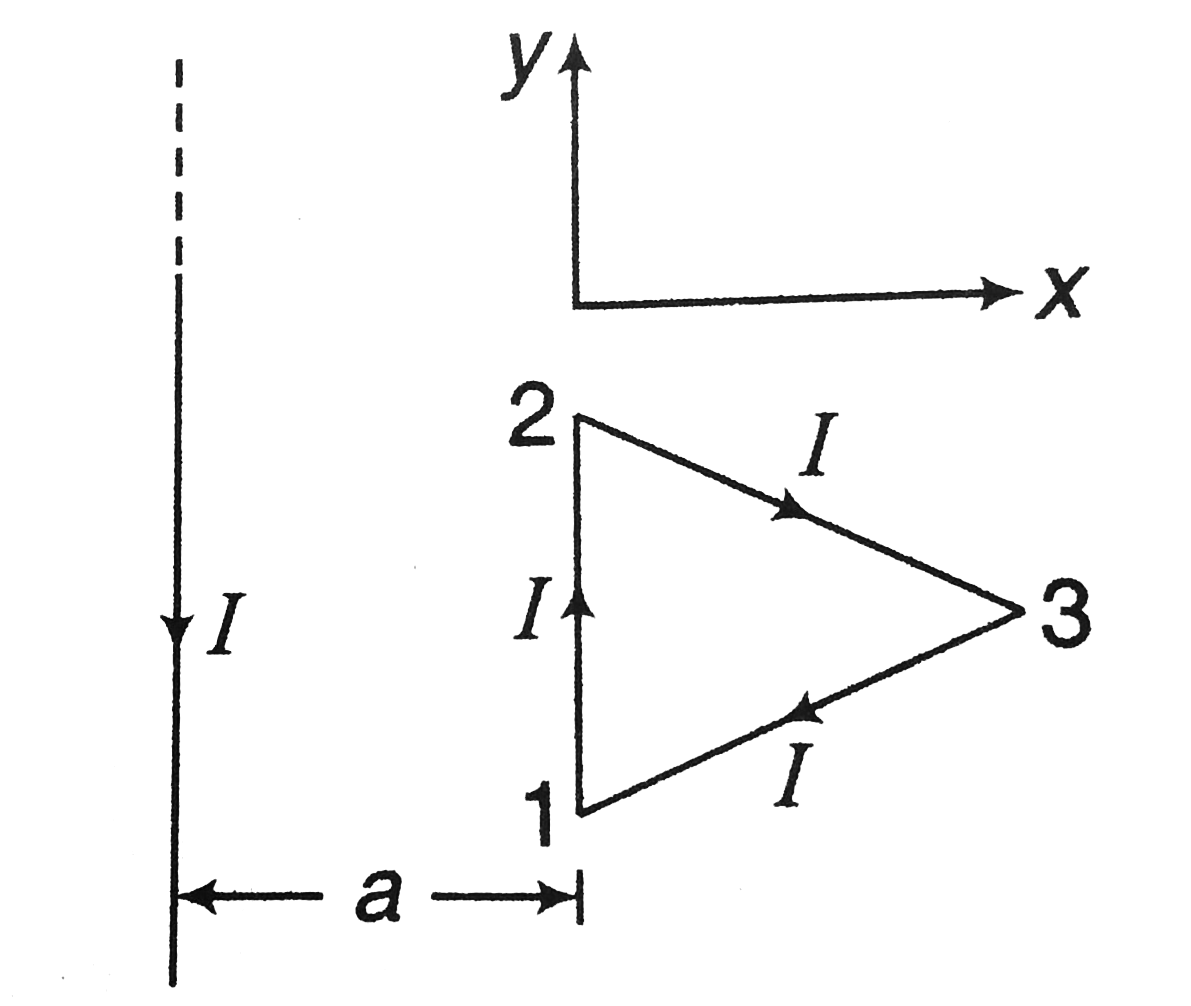
View SolutionAn equilateral triangular frame with side a carrying a current I is placed at a distance a from an infinitely long straight wire carrying a current I as shown in the figure. One side of the frame isparallel to the wire. The whole system lies in the xy-plane. Find the magnetic force F acting on the frame.
View SolutionA long straight wire is carrying a current of 25 A. A squre loop of side length 10 cm carrying a current of 15 A, is placed 2 cm from the wire as shown in figure. The force on the loop is

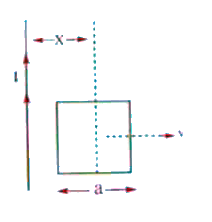
View SolutionA conducting square frame of side 'a' and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity 'V'. The emf induced in the frame will be proportional to
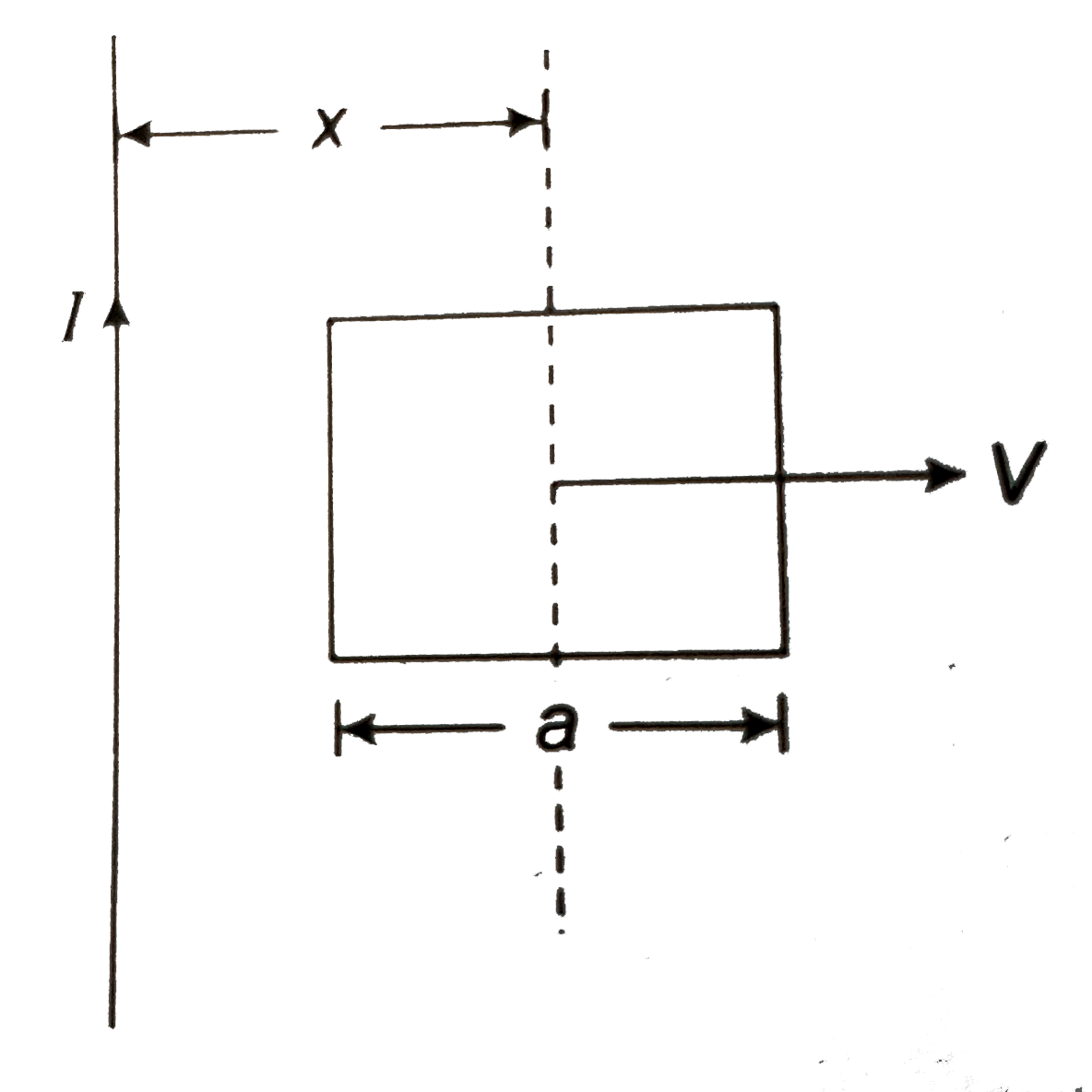
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
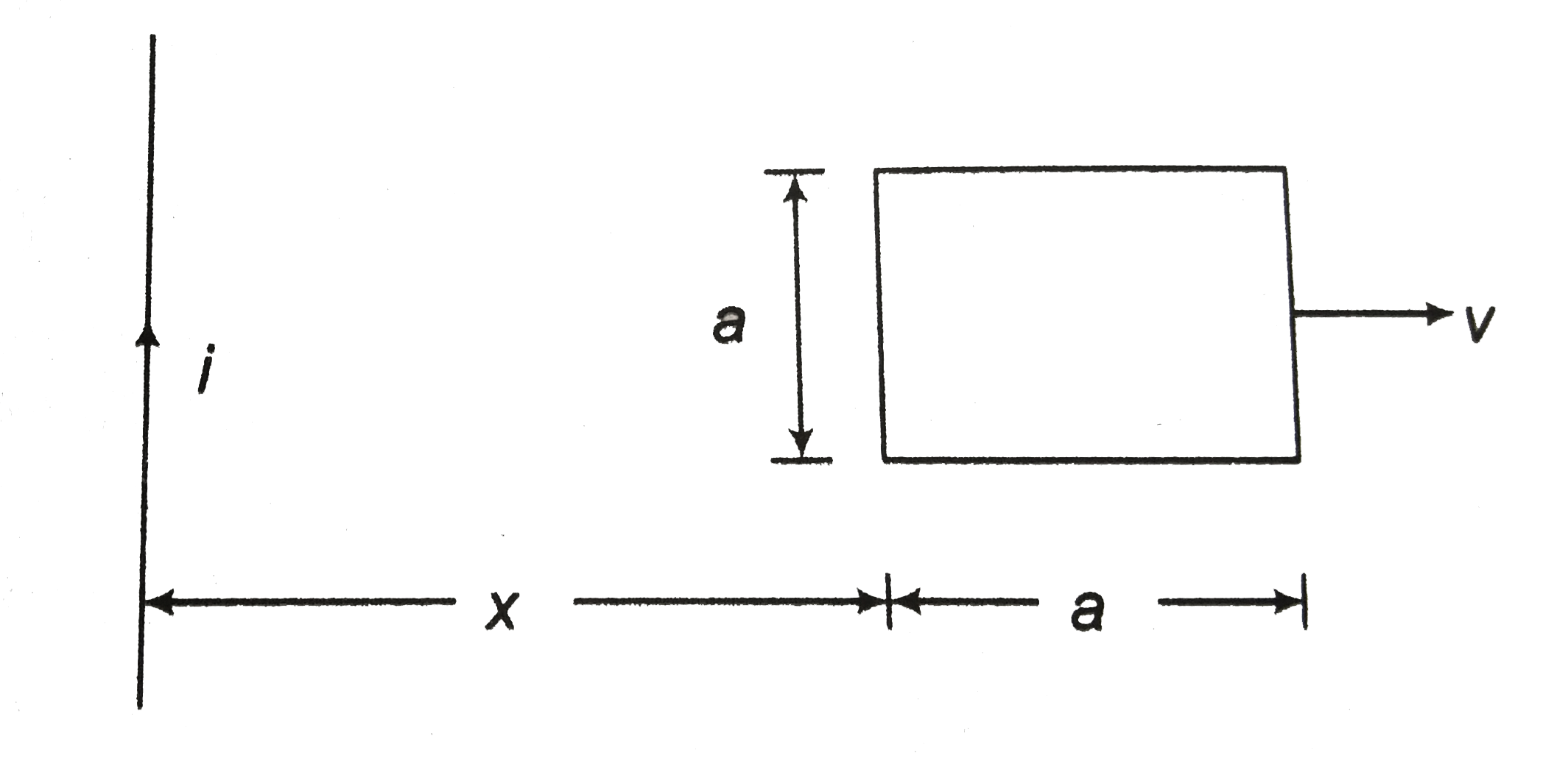
View SolutionA conducting square frame of side .a. and a long straight wire carrying currnet I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity .V.. The emf induced inthe frame will be proportional to
View SolutionA square loop of side a is placed at a distance a length away from a long wire carrying a current I1 . If the loop carries a current I2 as shown in the figure . Then the nature of the nature of the force and its amount is

View Solution
