The magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
μ0i4πd→l×→rr3
−μ0i4πr×→rr3
μ0i4πd→l×→rr3
−μ0i4πd→l×→rr1
The correct Answer is:C, D
Step by step video & image solution for The magnetic field at the origin due to a current element I (vec dl ) placed at a positon (vec r) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3 COMPREHENSION-1
5 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-3 COMPREHENSION-2
3 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-2
26 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
The magnetic field at the origin due to a current element I→dl placed at position r is
(i) (μ0i4π)(d→l×→rr3)
−(μ0i4π)(d→l×→rr3)
(iii) (μ0i4π)(→r×d→lr3)
−(μ0i4π)(→r×d→lr3)
View SolutionThe magnetic field at the origin due to the current flowing in the wire is

View SolutionThe magnetic field at the origin due to the current flowing in the wire is

View SolutionFind the field at the origin O due to the current i=2A.
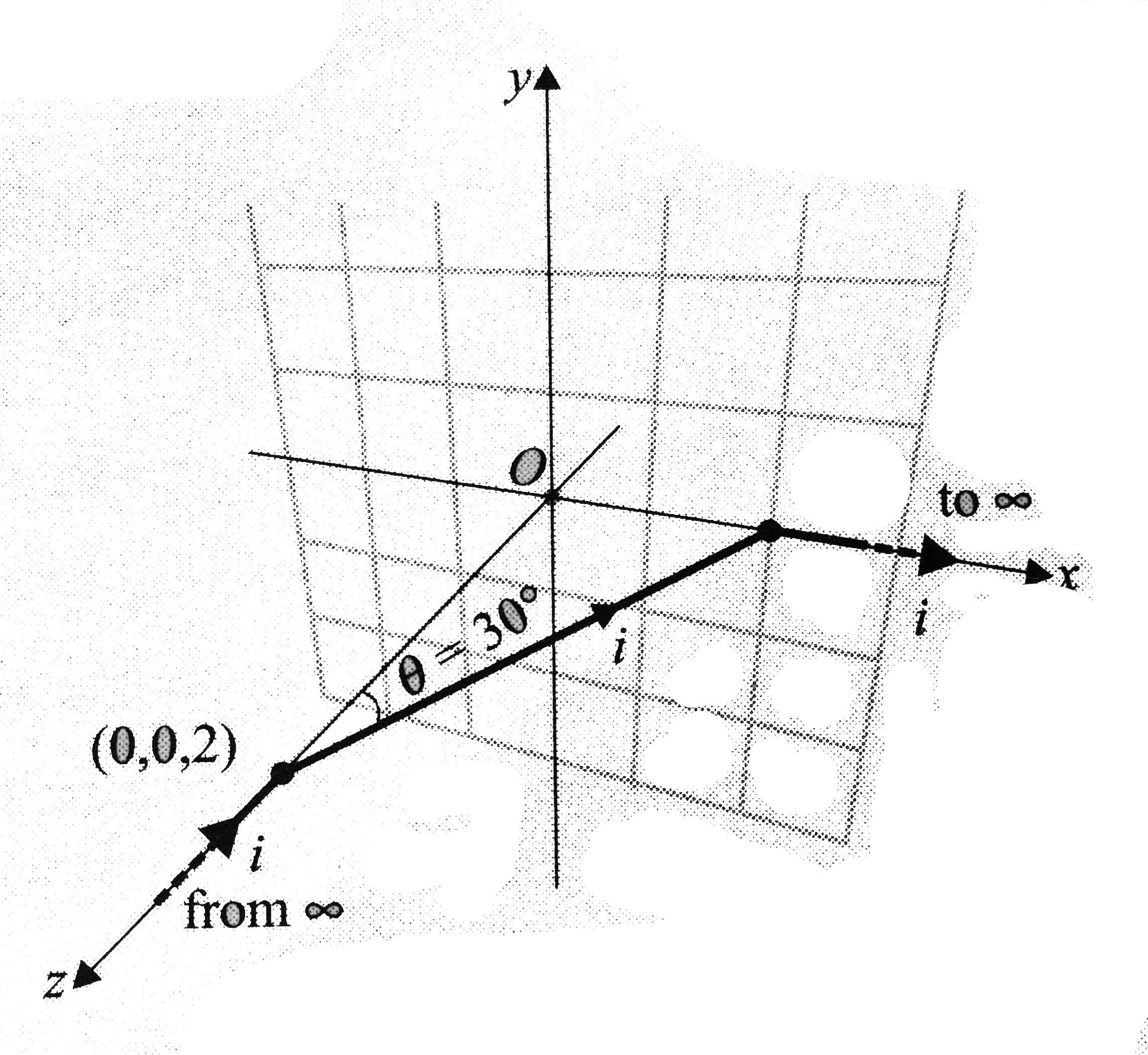
View SolutionThe magnetic field ¯¯¯¯¯dB due to a small current element ¯¯¯dl at a distance →r and carrying current 'I' is
View SolutionFind the magnetic field at the ccentre of a current carrying conductor bent in the form of an arc subtending angle θ at its centre. Radius of the arc is R
Strategy: Let the arc lie in x-y plane with its centre at the origin. Consider a small current element i→dl as shown. The field due to this element at the centre can be obtained by Biot-Savart law
View SolutionWhat is the magnetic field ∣∣→B∣∣ at the point P due to a current carrying wire of length AB (having a current of 2A) shown in figure ?
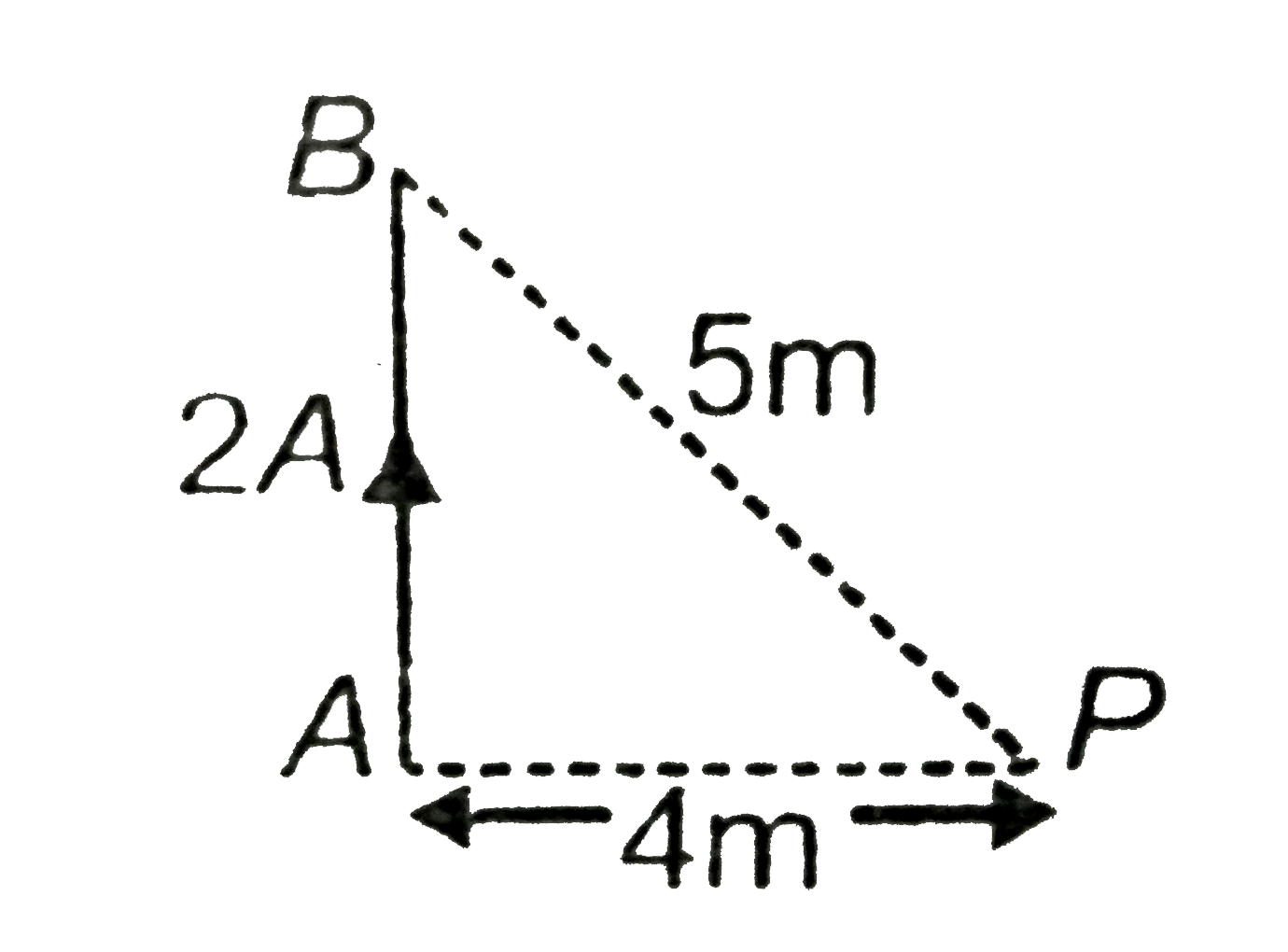
View SolutionA: In any magnetic field region the line integral ∮→B.→dl along a closed loop is always zero.
R: The magnetic field →B in the expressioin ∮→B.→dl is due to the currents enclosed only by the loop.
View SolutionThe electric field intensity →E , , due to an electric dipole of dipole moment →p , at a point on the equatorial line is :
View SolutionAn external magnetic field is decreased to zero, due to which a current is induced in a circular wire loop of radius r and resistance R placed in the field. This current will not become zero at the instant when B stops changing
View Solution