The magnetic field at the origin due to a current element I→dl placed at position r is
(i) (μ0i4π)(d→l×→rr3)
−(μ0i4π)(d→l×→rr3)
(iii) (μ0i4π)(→r×d→lr3)
−(μ0i4π)(→r×d→lr3)
μ0Id→l×→r4πr2
μ0I→r×d→l4πr2
μ0I→r×d→l4πr2
−μ0Id→l×→r4πr2
The correct Answer is:C, D
To find the magnetic field at the origin due to a current element Id→l placed at position →r, we can use the Biot-Savart law, which states that the magnetic field d→B due to a small current element is given by:
d→B=μ04πId→l×→rr3
where:
- μ0 is the permeability of free space,
- I is the current,
- d→l is the vector length of the current element,
- →r is the position vector from the current element to the point where the magnetic field is being calculated,
- r is the magnitude of the vector →r.
1. Identify the Variables:
- Let d→l be the vector representing the current element.
- Let →r be the position vector from the current element to the origin.
2. Apply the Biot-Savart Law:
- According to the Biot-Savart law, the magnetic field at the origin due to the current element is given by:
d→B=μ04πId→l×→rr3
3. Consider the Direction of the Cross Product:
- The direction of the magnetic field is determined by the right-hand rule applied to the cross product d→l×→r.
- If we reverse the order of the vectors in the cross product, we introduce a negative sign:
d→B=−μ04π→r×d→lr3
4. Identify the Correct Options:
- From the derived expressions, we can see that the magnetic field can be expressed in two forms:
- μ0I4πd→l×→rr3
- −μ0I4π→r×d→lr3
- Therefore, the correct answers from the options provided are:
- μ0I4πd→l×→rr3 (Option i)
- −μ0I4π→r×d→lr3 (Option iv)
Final Answer:
The magnetic field at the origin due to the current element Id→l placed at position →r is given by:
- μ0I4πd→l×→rr3 (Option i)
- −μ0I4π→r×d→lr3 (Option iv)
- μ0 is the permeability of free space,
- I is the current,
- d→l is the vector length of the current element,
- →r is the position vector from the current element to the point where the magnetic field is being calculated,
- r is the magnitude of the vector →r.
- Let d→l be the vector representing the current element.
- Let →r be the position vector from the current element to the origin.
- According to the Biot-Savart law, the magnetic field at the origin due to the current element is given by:
d→B=μ04πId→l×→rr3
- The direction of the magnetic field is determined by the right-hand rule applied to the cross product d→l×→r.
- If we reverse the order of the vectors in the cross product, we introduce a negative sign:
d→B=−μ04π→r×d→lr3
- From the derived expressions, we can see that the magnetic field can be expressed in two forms:
- μ0I4πd→l×→rr3
- −μ0I4π→r×d→lr3
- Therefore, the correct answers from the options provided are:
- μ0I4πd→l×→rr3 (Option i)
- −μ0I4π→r×d→lr3 (Option iv)
The magnetic field at the origin due to the current element Id→l placed at position →r is given by:
- μ0I4πd→l×→rr3 (Option i)
- −μ0I4π→r×d→lr3 (Option iv)
Similar Questions
The magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
View SolutionThe magnetic field ¯¯¯¯¯dB due to a small current element ¯¯¯dl at a distance →r and carrying current 'I' is
View SolutionThe magnetic field at a distance r from a long wire carryimg current I is 0.4 T. The magnetic field at a distance 2r is
View SolutionElectric potential due to a dipole at a position →r from its centre is: where (K=14πε0
View SolutionIf V=2r2 then find (i) →E(1,0,−2) (ii) →E(r=2)
View SolutionThe position vector of an object moving in X-Z plane is →r=v0tˆi+a0eb0tˆk.
Find its (i) velocity (→v=d→rdt) (ii) speed (|→v|) (iii) Acceleration (d→vdt) as a function of time.
View Solution(A) : A magnetic field is produced either by a steady current or by a time varying electric field (R) : According to Ampere’s law ∮¯¯¯B.¯dl=μ0i0+μ0ε0d∮Edt
View SolutionFind the unit vector of the vector →r=4ˆi−2ˆj+3ˆk
View SolutionA ball of radius R carries a positive charge throughout its volume, such that the volume density of charge depends on distance r from the ball's centre as ρ=ρ0(1−r®), where ρ0 is a constant. Assuming the permittivity of ball to be one , find magnitude of electric field as a function of distance r, both inside and outside the ball.
Strategy : The field has a spherical symmetry . For a point outside the ball (r>R)
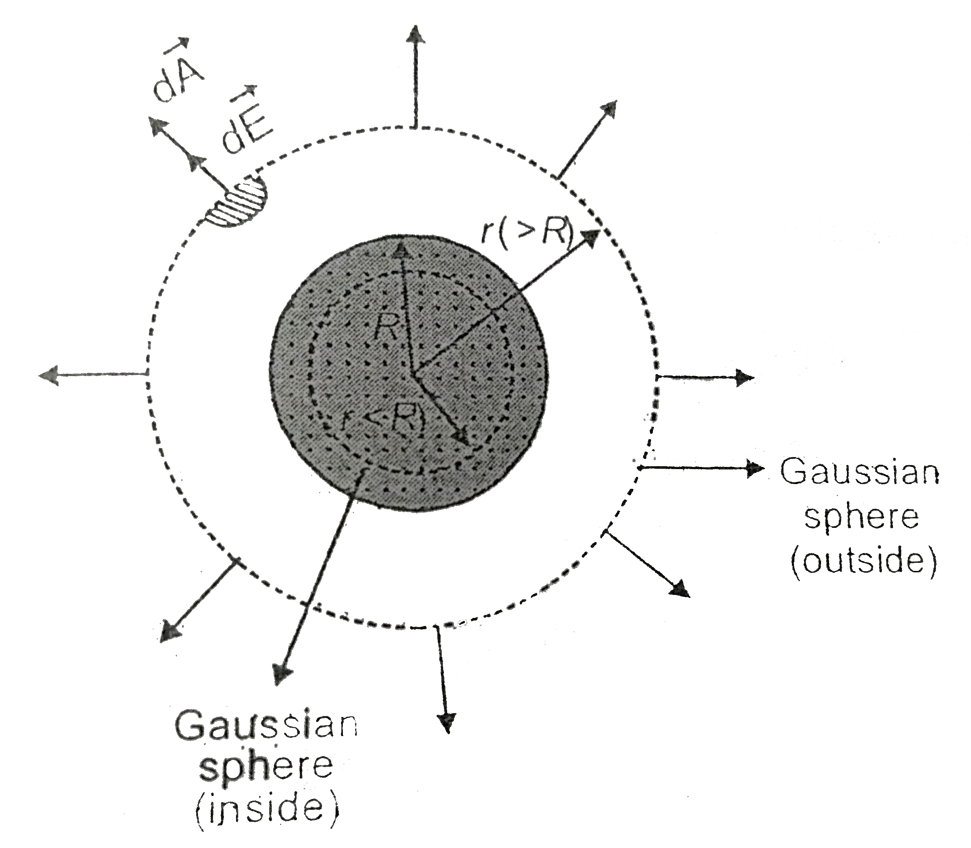
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law , ϕ=Qε0
⇒Eout=Q4πε0r2, where Q is total charge
For a point inside the ball (r<R)
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law, ϕ=qencε0
⇒Ein=qenc4πε0r2
where qenc= charge in a sphere of radius r(<R)
To find the enclosed charge , consider a spherical shell of radius r and thickness dr
Its volume dV=4πr2dr
Charge dq=ρdV
⇒dq=ρ0(1−rR)4πr2dr
⇒q=∫r0ρ0(1−rR)4πr2dr
=ρ04π[∫r0r2dr−∫r0r3Rdr]=ρ04π[r33−r44R]

View SolutionColumn- IColumn II(Operation of nonzero vectors→Pand→Q)(Possivle angle between→Pand→Q)(A)∣∣→P×→Q∣∣=0(P) 90∘(B)∣∣→P×→Q∣∣=√3→P.→Q(Q) 180∘(C)→P+→Q=→RandP+Q=R(R) 60∘(D)∣∣→P+→Q∣∣=∣∣→P−→Q∣∣(S) 0∘(T) 30∘
View Solution
