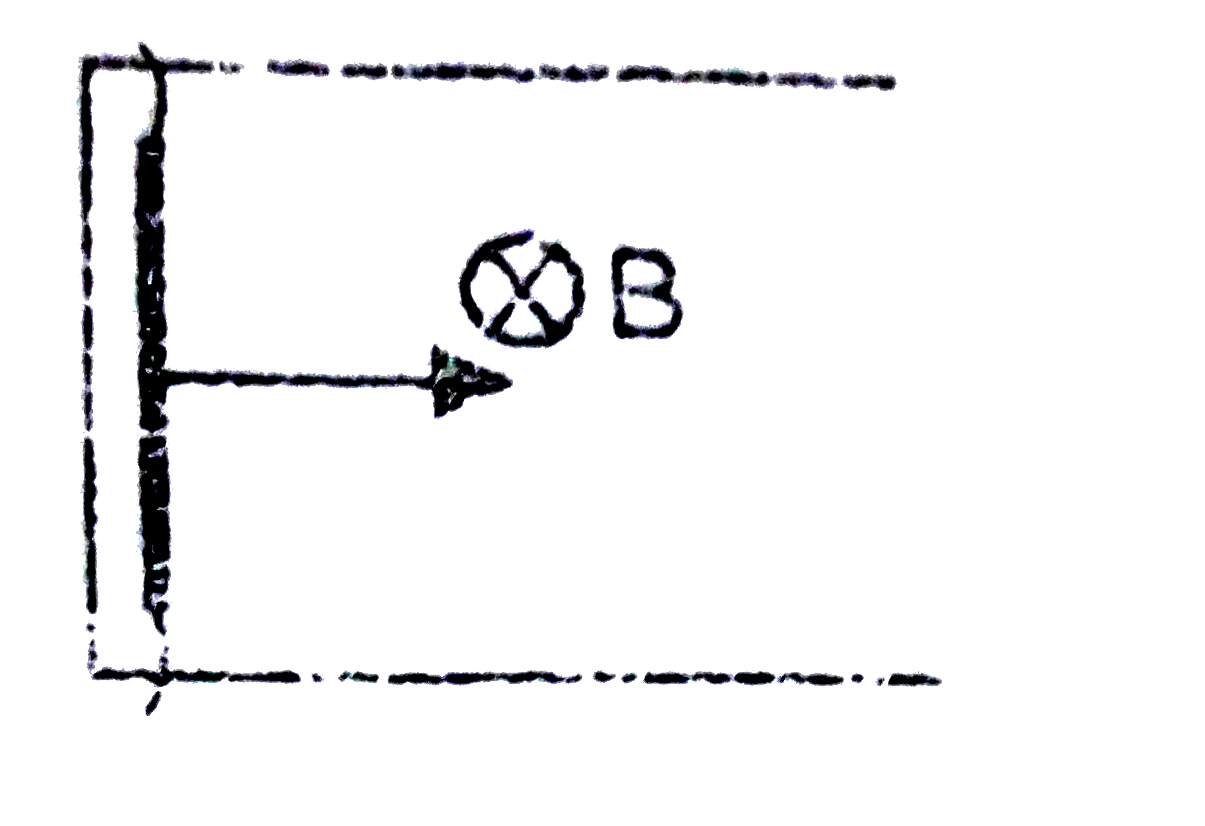
A II-shaped conductor is located in a uniform magnetic field perpendicular to the plane of the conductor and varying with time at the rate dBdt=0.10T/s.A conducting connectors starts moving with a constant acceleration w=10cm/s2 along the parallel bars of the conductor.The length of the connector is equal to l=20cm.Find the emf induced (in mV) in the loop t=2.0s after the beginning of the motion.If at the moment t=0 the loop area and the magnetic induction (B) are equal to zero.The self inductance of the loop is to be neglected.
The correct Answer is:A, B
ε=dϕdt=AdBdt+BdAdt=(lx)dBdt+B(Vl)⇒ε1=3/2ωldBdtt2=12mV.

Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 3
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 4
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
14 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
In a uniform magnetic field, a π shaped metal frame is located perpendicular to the plane of the conductor and varying with time at the rate (dB/dt)=0.20T/s. A conducting connector starts moving with an acceleration a=30cm/s2 along the parallel bars of the frame. The length of the connector is equal to l = 44 cm. Find the emf induced in the loop t = 1 s after the beginning of the motion, if at the moment t = 0, the loop area and the magnetic induction are equal to zero.
View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is

View Solution
Knowledge Check
A conducting circular loop is placed in a uniform magnetic field, B=0.025T with its plane perpendicular to the loop. The radius of the loop is made to shrink at a constant rate of 1mms−1. The induced emf when the radius is 2cm is
A2πμVBπμVCπ2μVD2μV
A rectangular loop with a sliding conductor of length l is located in a uniform magnetic field perpendicular to the plane of the loop . The magnetic induction is b. The resistances R1 and R2, respectively. Find the current through the conductor during its motion to the right with a constant velocity v.

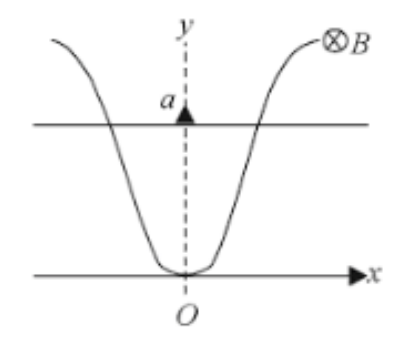
View SolutionA wire bent as a parabola y=kx2 is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane xy. At t=0, the sliding wire starts sliding from the vertex O with a constant acceleration a linearly as shown in Fig. Find the emf induced in the loop -
View SolutionA rectangular conductor LMNO is place in a uniform magnetic field of 0.5 T Fig. The field is directed perpendicular to the plane to the conductor. When the arm MN of length 20 cm is moved with a velocity of 10 m/s calculate the emf induced in the arm. Find the value of induced current if resistance of arm MN is 5 Ohm

View SolutionA rectangular loop with a sliding conductor of length l is located in a uniform magnetic field perpendicular to the plane of loop. The magnetic induction perpendicular to the plane of loop Is equal to B. The part ad and be has electric resistance R1 and R2, respectively. The conductor starts moving with constant acceleration a0, at time t=0. Neglecting the self-inductance of the loop and resistance of conductor. Find

(a) the current through the conductor during its motion.
(b) the polarity of abcd terminal.
(c) external force required to move the conductor with the given acceleration.
View SolutionA straight conductor 0.1 m long moves in a uniform magnetic field 0.1 T. The velocity of the conductor is 15ms−1 and is directed perpendicular to the field. The emf induced between the two ends of the conductor is
View SolutionA conducting circular loop is placed is a uniform magnetic field B =0.20 T with its plane perpendicular to the field . Somehow, the radius of the loop starts shrinking at a constant rate of 1.0mms−1. Find the induced emf in the loop at an instant when the radius is 2 cm.
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is constant and t is time. The induced current flowing through loop is

View Solution
