A closed circuit consists of a source of constant emfE and a choke coil of inductance L connected in series.The active resistance of the whole circuit is equal to R.It is in steady state.At the moment L=0 the choke coil inductance was decreased abruptly 4 times.The current in the circuit as a function of time t is ER[1−xc−4tR/L].Find out value of x.
The correct Answer is:C
To solve the problem, we need to analyze the circuit consisting of a constant EMF source E, a choke coil with inductance L, and a resistance R. The choke coil's inductance is abruptly decreased to L4. We are given the expression for the current in the circuit as a function of time t:
I(t)=ER(1−xe−4RtL)
We need to find the value of x.
1. Write the Circuit Equation:
The voltage across the inductor and the resistor must equal the EMF. According to Kirchhoff's voltage law, we can write:
E=IR+LdIdt
2. Substituting Inductance:
Since the inductance is decreased to L4, we substitute this into the equation:
E=IR+L4dIdt
3. Rearranging the Equation:
Rearranging gives us:
L4dIdt=E−IR
4. Separating Variables:
We can express this as:
dIE−IR=4Ldt
5. Integrating Both Sides:
Integrate both sides. The left side can be integrated using the natural logarithm:
∫dIE−IR=−1Rln|E−IR|+C1
The right side integrates to:
∫4Ldt=4Lt+C2
6. Combining Constants:
Setting the constants equal gives:
−1Rln|E−IR|=4Lt+C
7. Solving for Current:
Exponentiating both sides leads to:
E−IR=Ke−4Lt
where K is a constant determined by initial conditions.
8. Finding the Current:
Rearranging gives:
I=ER−KRe−4Lt
Let K=3E (based on the steady state where I approaches ER):
I=ER−3ERe−4Lt
Therefore:
I=ER(1−3e−4Lt)
9. Comparing with Given Expression:
Now we compare this with the given expression:
I(t)=ER(1−xe−4RtL)
From this comparison, we see that x=3.
Final Answer:
The value of x is 3.
The voltage across the inductor and the resistor must equal the EMF. According to Kirchhoff's voltage law, we can write:
E=IR+LdIdt
Since the inductance is decreased to L4, we substitute this into the equation:
E=IR+L4dIdt
Rearranging gives us:
L4dIdt=E−IR
We can express this as:
dIE−IR=4Ldt
Integrate both sides. The left side can be integrated using the natural logarithm:
∫dIE−IR=−1Rln|E−IR|+C1
The right side integrates to:
∫4Ldt=4Lt+C2
Setting the constants equal gives:
−1Rln|E−IR|=4Lt+C
Exponentiating both sides leads to:
E−IR=Ke−4Lt
where K is a constant determined by initial conditions.
Rearranging gives:
I=ER−KRe−4Lt
Let K=3E (based on the steady state where I approaches ER):
I=ER−3ERe−4Lt
Therefore:
I=ER(1−3e−4Lt)
Now we compare this with the given expression:
I(t)=ER(1−xe−4RtL)
From this comparison, we see that x=3.
The value of x is 3.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 310videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 46videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 114videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems31videos
ELECTRODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP40videos
ELECTROSTATICS
Similar Questions
A closed circuit consits of a source of constant and E and a choke coil of inductance L connected in series. The active resistance of the whole circuit is equal to R. At the moment t=0 the choke coil inductance was decreased abrupty η times. FInd the current in the circuit as a function of time t.
View SolutionA closed circuit of a resistor R, inductor of inductance L and a source of emf E are connected is series. If the inductance of the coil is abruptly decreaed to L/4 (by removing its magnetic core), the new current immediately after this moment is (before decreasing the inductance the circuit is in steady state)
View SolutionAn L-R circuit has a cell of e.m.f. E , which is switched on at time t = 0. The current in the circuit after a long time will be
View SolutionA coil of inductance 0.20H is connected in series with a switch and a cell of emf 1.6V. The total resistance of the circuit is 4.0Ω. What is the initial rate of growth of the current when the switch is closed?
View SolutionIn the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
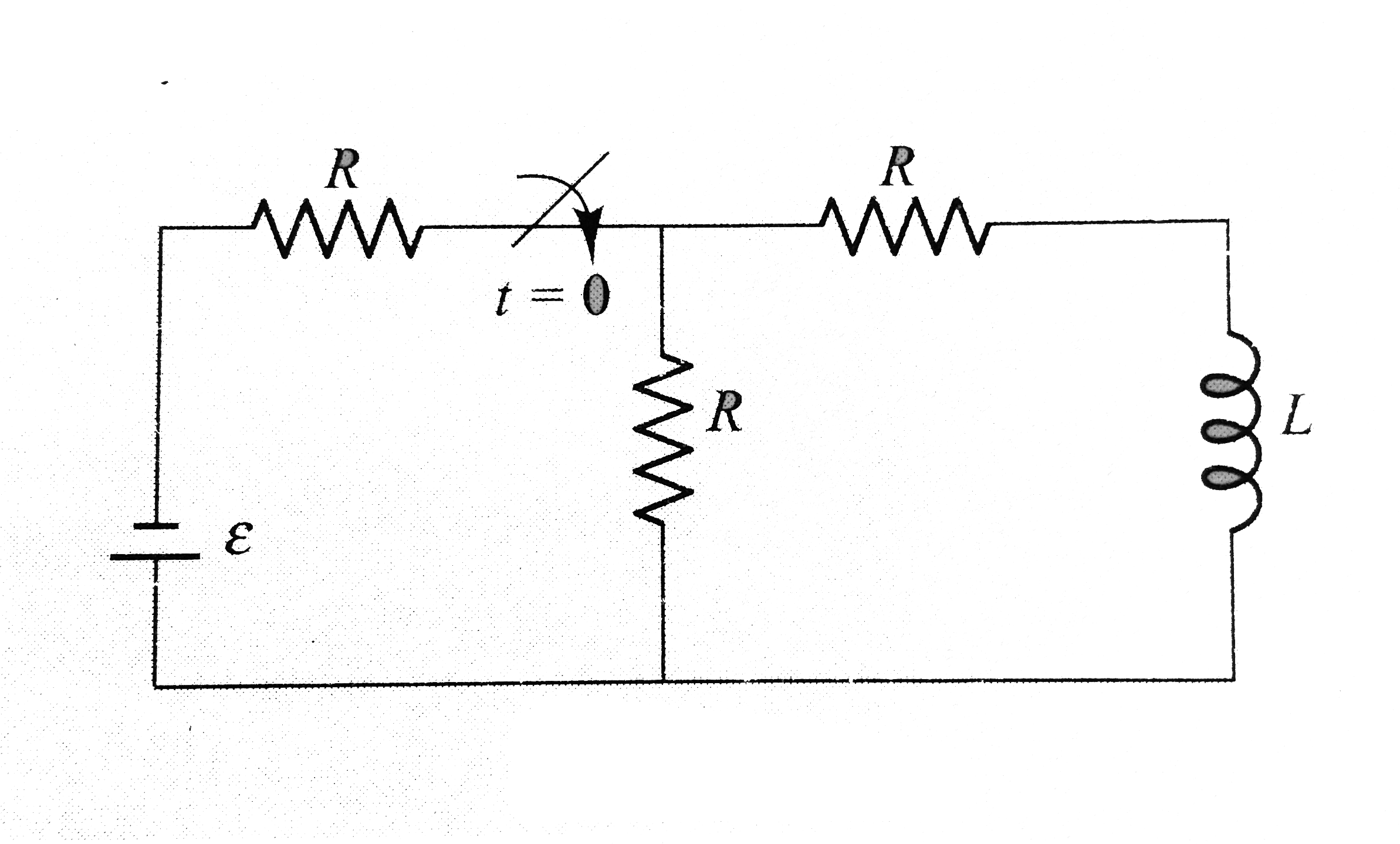 View Solution
View SolutionAn indcutor having self inductance L with its coil resistance R is connected across a battery of emf elipson. When the circuit is in steady state t = 0, an iron rod is inserted into the inductor due to which its inductance becomes nL (ngt1).
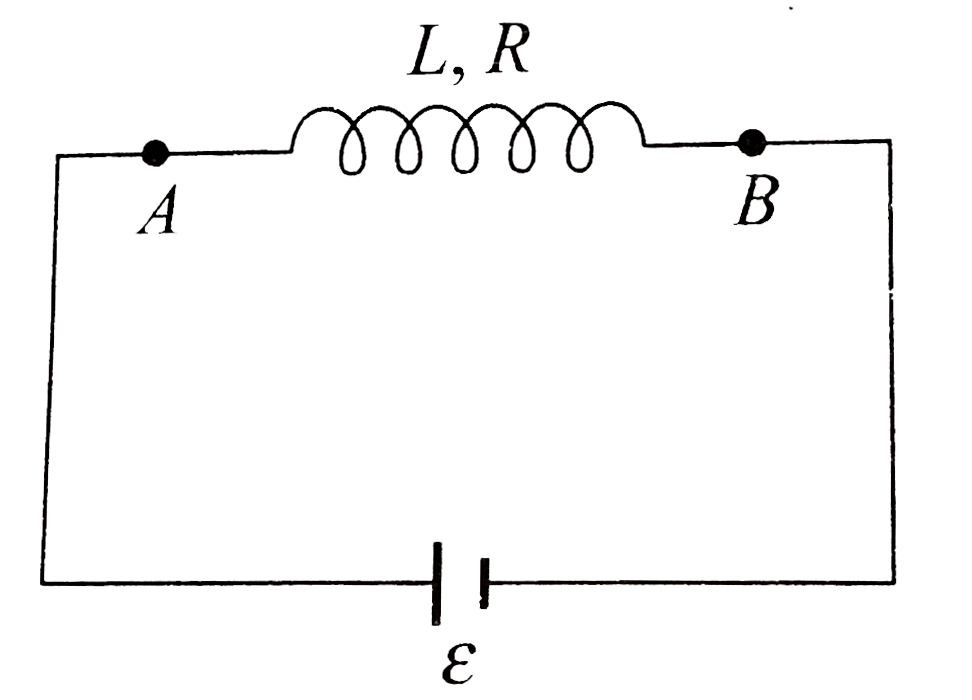
after insertion of rod, current in the circuit:View SolutionIn the following circuit the switch is closed at t=0.Intially there is no current in inductor.Find out current the inductor coil as a function of time.
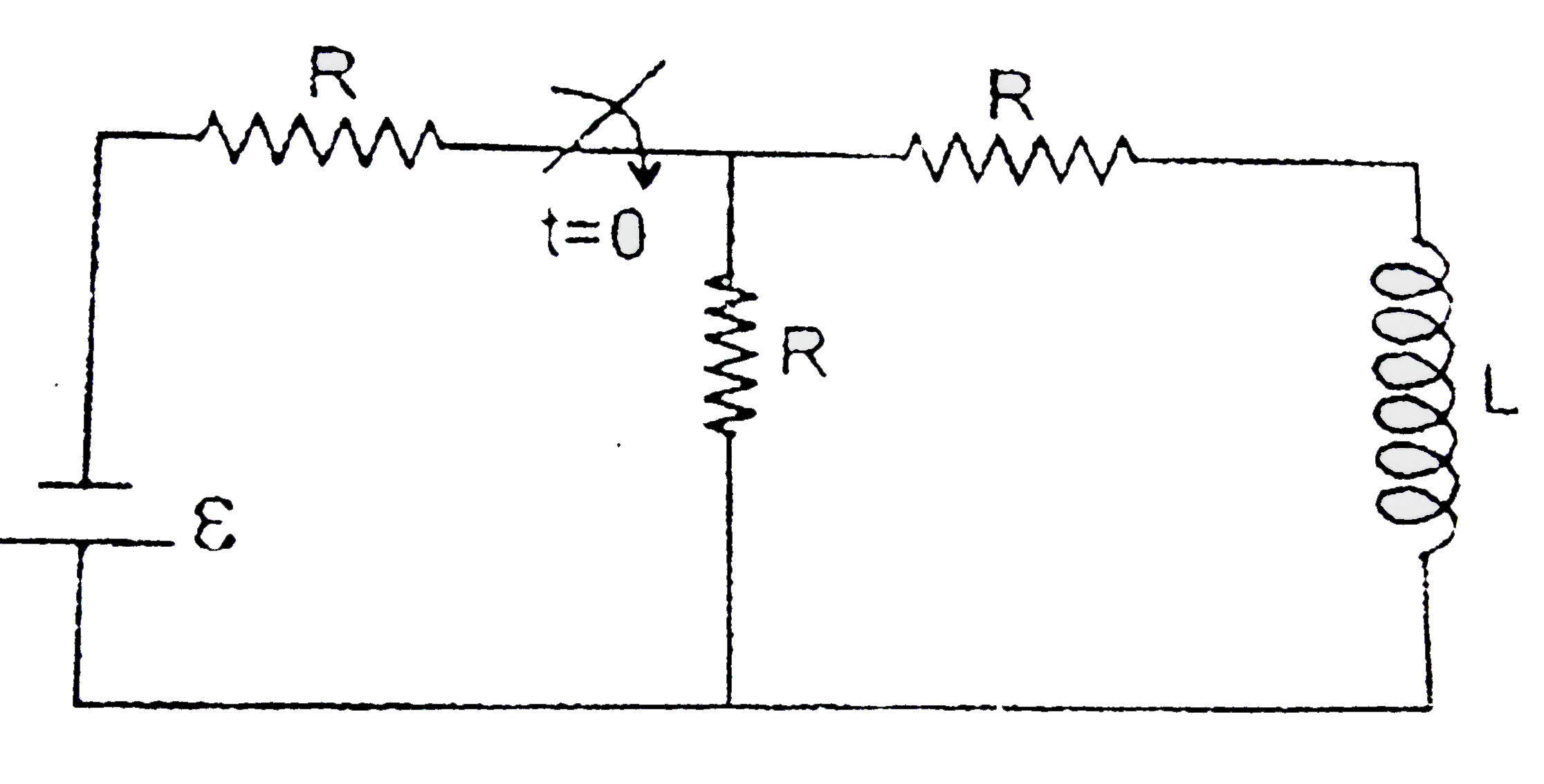 View Solution
View SolutionA coil of inductance 0.01 H is connected in series with a capacitor of capacitance 25μF with an AC source whose emf is given by E = 310 sin 314t (volt). What is the reactance of the circuit ?
View SolutionWhen a choke coil carrying a steady current is short circuited, the current in it decreases to β(<1) times its initial value in a time T. The time constant of the choke coil is
View SolutionTwo coils of self inductance L1 and L2 are connected in parallel and then connected to a cell of emf ε and internal resistance - R. Find the steady state current in the coils.
View Solution

